基本概念：
1、状态方程：
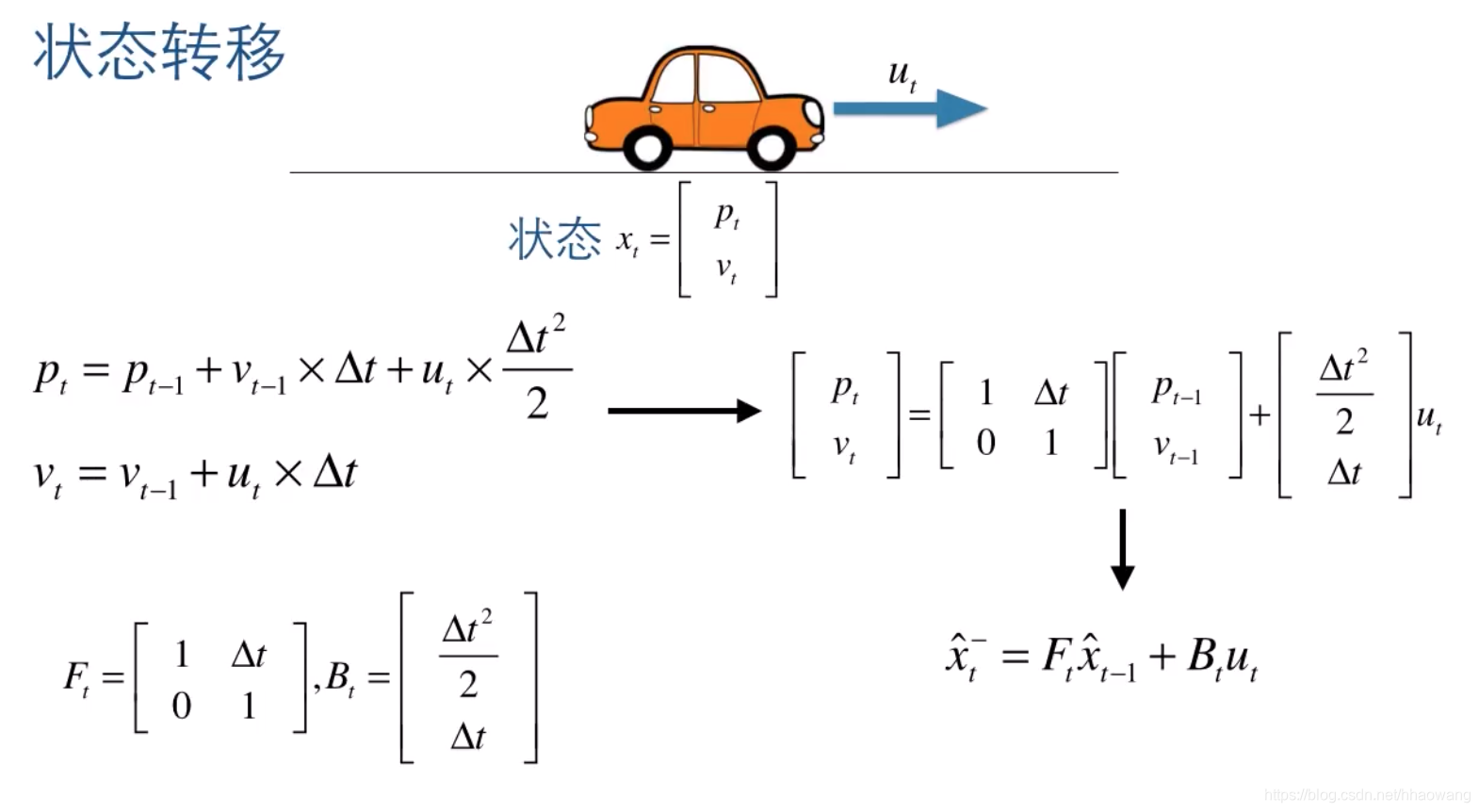
某一时刻的状态用Xt表示，它是一个列向量，表征了当前位置Pt和当前速度Vt；上一时刻位置Pt-1和上一时刻速度Vt-1，由于卡尔曼滤波器是时域下的线性滤波器，故可以对状态矢量Xt进行改写：
-
状态预测公式：
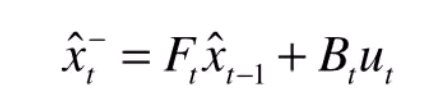，x^ 表示预测值或推测值，非实际值
-
状态转移矩阵Ft, 表示如何从上一时刻的状态来推测当前时刻的状态：
-
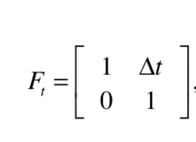
控制矩阵B，表示控制量U如何作用与当前状态：
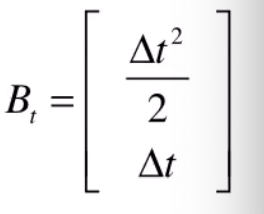
有了状态预测公式我们就可以推测当前时刻的状态，但是我们知道所有的推测都是包含噪声的，噪声越大，则不确定性就越大，准确度越低；如何衡量这种不确定性的大小呢，协方差矩阵可以完成这项表征任务。
2.协方差矩阵 ：
对于一维包含噪声的数据，它的分布可以近似地用高斯分布来表示：
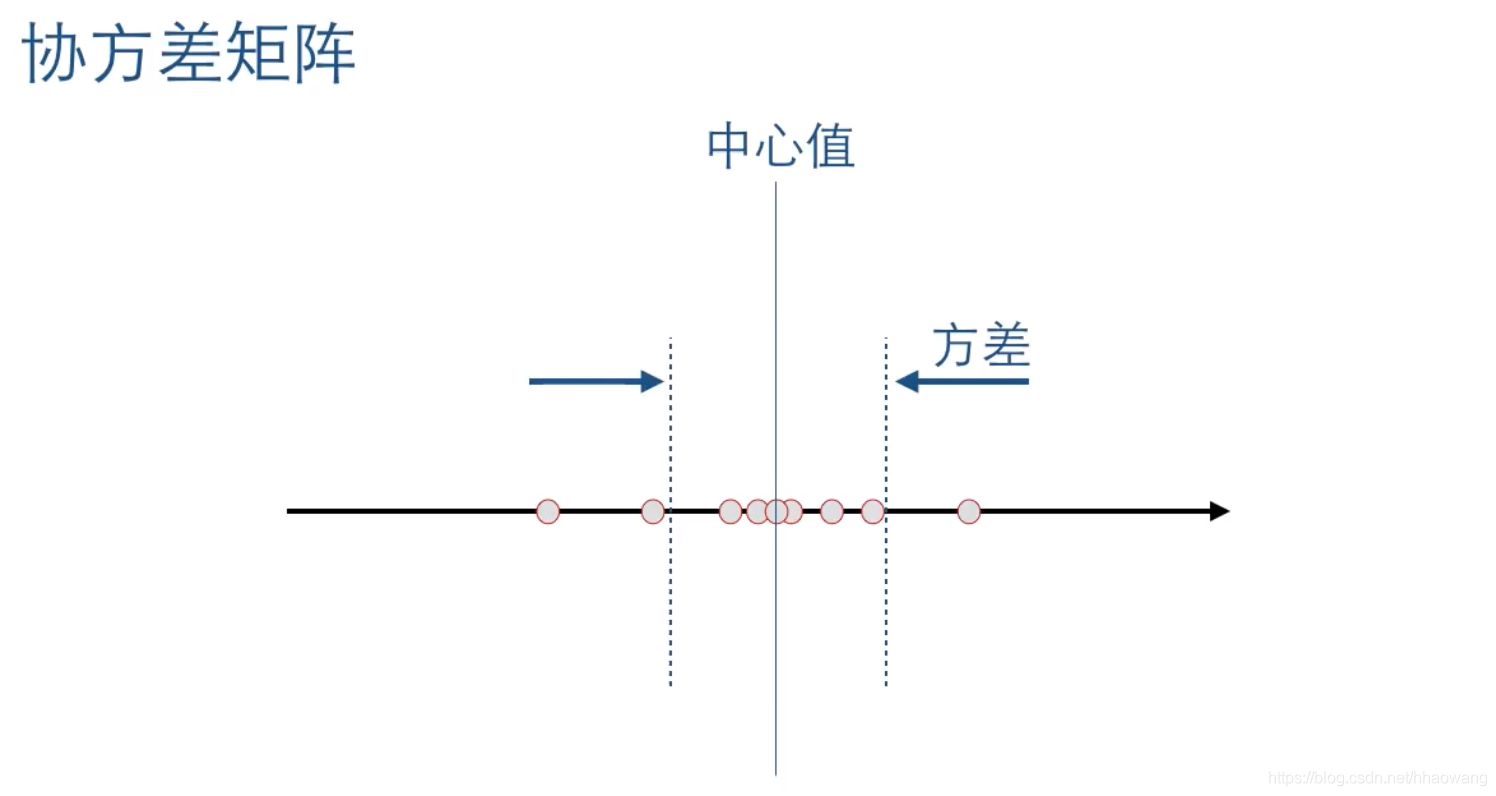
期望值即为预测的输出值，而其他离散的点就是噪声点，不难发现，噪声点的离散程度会影响样本的均值与方差，这也就导致了状态预测出现了偏差。
二维包含噪声数据，它在x，y轴均满足高斯分布，则：
（1） x，y独立同分布 （2） x，y正相关 （3） x，y负相关
因此，二维问题不能简单的用两个维度的高斯分布来表征，还需要考虑两个维度之间的相关性，即协方差。
协方差矩阵可以表示为：
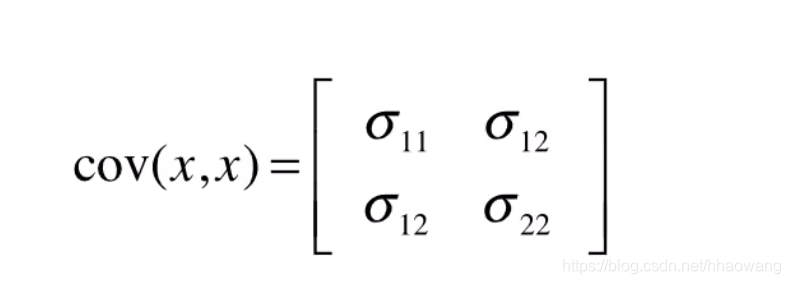
在卡尔曼滤波器中，所有关于噪声或不确定性的表征，都要用到协方差矩阵。在小汽车的例子中，每一个时刻的状态不确定性都是由协方差矩阵P来表示，那么，如何让这种不确定性在每一个时刻进行传递呢？方法就是让协方差矩阵乘以一个状态转换矩阵。
值得注意的是，我们的预测模型也不是绝对准确的，它也存在一些不确定性或者误差，因此，需要将模型引入的不确定性考虑在内。
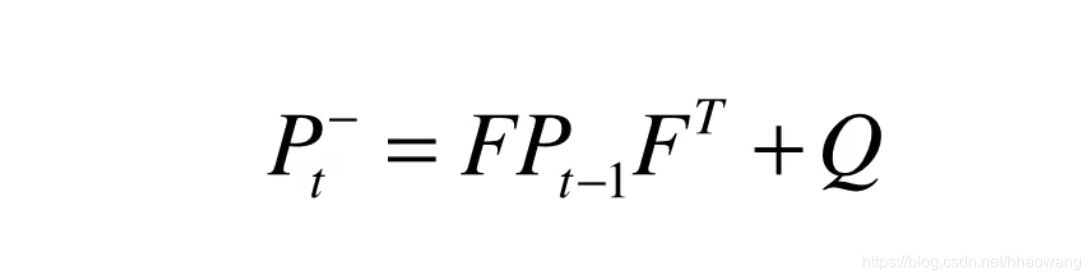
上式描述了，不确定性在不同时刻的传递特性。
假设在小车的一端，有一个观测器用来观测小车的每一个时间点的位置，这个观测值记为标量Zt，状态向量Xt为列向量
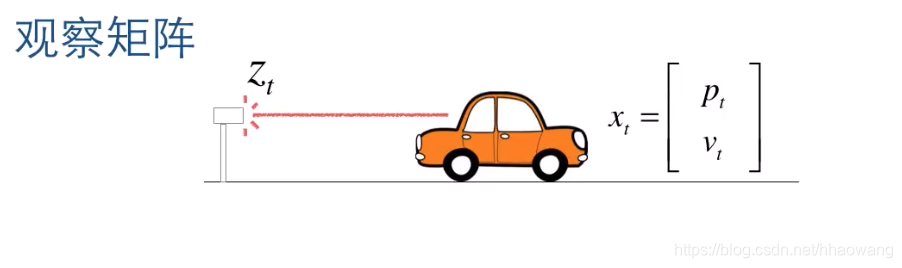
则Zt可以用Xt表示为：
由于观测值Z存在观测误差，引入了不确定性，用v来表示这种不确定性。
3.多传感器融合策略：
假设观测器不止一个或一种，例如：激光测距仪+IMU+红外等等，因此，观测值Z就成了一个多维的列向量，它包含了多个观测器的观测值。而每一个测量值，都只是真实状态的不完全表征，我们可以从几种不完全的表征中推断出真实的状态，而卡尔曼滤波器的数据融合功能，正是在测量矩阵中体现出来的。我们已经有了观测量Z和它的协方差矩阵R，那么如何将他们整合至系统状态估计呢？上述，已经得到了带偏差的状态估计值：假设观测器不止一个或一种，例如：激光测距仪+IMU+红外等等，因此，观测值Z就成了一个多维的列向量，它包含了多个观测器的观测值。而每一个测量值，都只是真实状态的不完全表征，我们可以从几种不完全的表征中推断出真实的状态，而卡尔曼滤波器的数据融合功能，正是在测量矩阵中体现出来的。
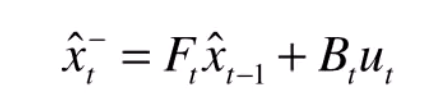… (1)
那么，在带偏差估计值得基础上，加上一个修正值便可以得到最佳估计值：
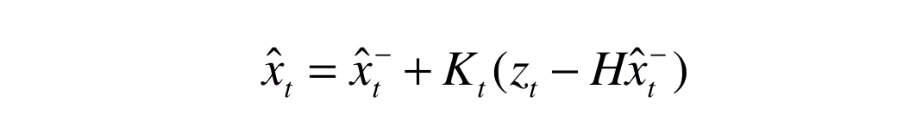
其中，
表示观测值Z与估计值之间的残差，Kt是卡尔曼系数，实际上它也是一个矩阵。
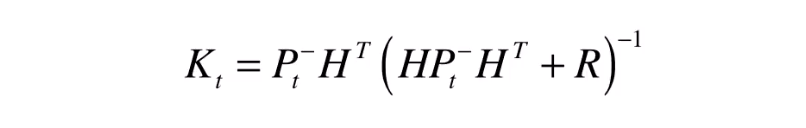
卡尔曼系数作用：
-
权衡 预测状态协方差矩阵P与观察量的协方差R的大小，来决定预测模型和观测模型的置信区间。若相信预测模型大于观测模型，残差的权重就会小一点；若相信观测模型大于预测模型，则残差权重就会大一点。
-
把残差的表现形式从观察域转换到状态域。
噪声协方差矩阵的更新：
更新最佳估计值得噪声分布，这个值用于下一时刻迭代。在这一步里，状态的不确定性经过滤波而减小，而下一时刻，由于噪声的引入，状态预测的不确定性又会增加，实际上，卡尔曼滤波正是在这种波动迭代过程中找到一个权衡。
4.总结：
预测：通过上一时刻预测得到了当前时刻的状态预测值，但这并不是最佳的估计值，需要从当前时刻的观测值获得信息，校正预测值；
更新：将观测值引入到状态估计中，在预测值更新后，便得到了最佳的状态预测值。
5.MATLAB卡尔曼滤波器的实现
Z —匀速运动的观测值，每秒1m的速度前进；
Noise – -高斯噪声
X — 初始状态
P — 状态协方差阵
F — 状态转移矩阵
Q — 状态转移矩阵的协方差阵，Q的方差较小，因为状态转移矩阵不易出现偏差。
H — 观测矩阵
R — 观测噪声方差
迭代次数100次的结果：
#include
#include
MPU6050 mpu; //实例化一个 MPU6050 对象，对象名称为 mpu
int16_t ax, ay, az, gx, gy, gz;
//********************global_angle data*********************//
float Gyro_y; //Y轴陀螺仪数据暂存
float Gyro_x; //X轴陀螺仪数据暂存
float Gyro_z; //Z轴陀螺仪数据暂存
float angleAx;
float angle6;
float K1 = 0.05; // 对加速度计取值的权重
float Angle; //一阶互补滤波计算出的小车最终倾斜角度
float accelz = 0;
//********************angle data*********************//
//***************Kalman_Filter Initialiation*********************//
float P[2][2] = {
{ 1, 0 },
{ 0, 1 }
};
float Pdot[4] = { 0, 0, 0, 0};
float Q_angle = 0.001, Q_gyro = 0.005; //角度数据置信度,角速度数据置信度
float R_angle = 0.5 , C_0 = 1;
float q_bias, angle_err, PCt_0, PCt_1, E, K_0, K_1, t_0, t_1;
float timeChange = 5; //滤波法采样时间间隔，单位毫秒ms
float dt = timeChange * 0.001; //注意：dt的取值为滤波器采样时间,单位秒s
//***************Kalman_Filter*********************//
void AngleFilter()
{
//平衡参数
Angle = atan2(ay , az) * 57.3; //角度计算公式
Gyro_x = (gx - 128.1) / 131; //角度转换
Kalman_Filter(Angle, Gyro_x); //卡曼滤波
//旋转角度Z轴参数
if (gz > 32768) gz -= 65536; //强制转换2g 1g
Gyro_z = -gz / 131; //Z轴参数转换
accelz = az / 16.4;
angleAx = atan2(ax, az) * 180 / PI; //计算与x轴夹角
Gyro_y = -gy / 131.00; //计算角速度
//一阶互补滤波
angle6 = K1 * angleAx + (1 - K1) * (angle6 + Gyro_y * dt);
}
kalman filter/
float angle, angle_dot; //平衡角度值angle，平衡角速度值angle_dot
void Kalman_Filter(double angle_m, double gyro_m)
{
angle += (gyro_m - q_bias) * dt;
angle_err = angle_m - angle;
Pdot[0] = Q_angle - P[0][1] - P[1][0];
Pdot[1] = - P[1][1];
Pdot[2] = - P[1][1];
Pdot[3] = Q_gyro;
P[0][0] += Pdot[0] * dt;
P[0][1] += Pdot[1] * dt;
P[1][0] += Pdot[2] * dt;
P[1][1] += Pdot[3] * dt;
PCt_0 = C_0 * P[0][0];
PCt_1 = C_0 * P[1][0];
E = R_angle + C_0 * PCt_0;
K_0 = PCt_0 / E;
K_1 = PCt_1 / E;
t_0 = PCt_0;
t_1 = C_0 * P[0][1];
P[0][0] -= K_0 * t_0;
P[0][1] -= K_0 * t_1;
P[1][0] -= K_1 * t_0;
P[1][1] -= K_1 * t_1;
angle += K_0 * angle_err; //角度, angle
q_bias += K_1 * angle_err;
angle_dot = gyro_m - q_bias; //角速度 angle_dot
} // kalman filter END //
void setup() {
// join I2C bus (I2Cdev library doesn't do this automatically)
Wire.begin();
// initialize serial communication
// (38400 chosen because it works as well at 8MHz as it does at 16MHz, but
// it's really up to you depending on your project)
Serial.begin(9600);
// initialize device
Serial.println("Initializing I2C devices...");
mpu.initialize();
// verify connection
Serial.println("Testing device connections...");
Serial.println(mpu.testConnection() ? "MPU6050 connection successful" : "MPU6050 connection failed");
} // setup END
void loop() {
mpu.getMotion6(&ax, &ay, &az, &gx, &gy, &gz); //IIC获取MPU6050六轴数据 ax ay az gx gy gz
AngleFilter(); //获取angle 角度和卡曼滤波
Serial.print(ax);Serial.print(",");
Serial.print(ay);Serial.print(",");
Serial.print(az);Serial.print("---");
Serial.print(angle);Serial.print(",");
Serial.print(angle_dot);Serial.print(",");
Serial.println(angle6);
delay(5);
} // Loop END
