本文转载自微信公众号ROBOTICS
在很久很久以前的那篇《位置角度平移旋转:“乱七八糟”的坐标变换》里,CC着重讲了如何用旋转矩阵表示坐标的旋转变换关系,并蜻蜓点水般提到了欧拉角、转轴转角和四元数的存在。有不少朋友都表示希望CC写一写空间姿态的各种表示方法的——现在,就让我们来把这个坑填上吧。
旋转矩阵复习
首先我们还是把旋转矩阵复习一下,希望你还记得下面这个式子:

这个式子说,有A、B两个坐标系,从B坐标到A坐标的旋转变换可以由这个R矩阵表示;其中,R矩阵的每一列分别是B坐标的x, y, z轴在A坐标中的表示;而由于旋转矩阵的转置正是其逆,R矩阵的每一行则分别是A坐标的x, y, z轴在B坐标中的表示。
比如说,如下两个坐标系,我们可以直接把R写出来:第一列,因为XB轴与ZA轴重合,所以是[0; 0; 1];第二列,YB轴与YA轴方向正好相反,所以是[0; -1; 0];同理,第三列是[1; 0; 0]。如果按照每一行来写,则第一行是与ZB重合的XA轴[0,0,1],第二行是与YB轴反方向的YA轴[0, -1, 0],第三行则是与XB轴重合的ZA轴[1, 0, 0]。

用旋转矩阵表示两个坐标系之间的旋转变换固然方便,但我们不禁要问,明明只是三个自由度的变换,为什么要用到九个数呢?
假如你在操控一架飞机,要拉升机头5度、或者向左倾斜机身10度,是不是还要先把这样的指令转为旋转矩阵呢?
在控制系统中,已知物体当前的姿态和理想的姿态,我们又要怎么计算姿态误差呢?
因为这种种的需求,我们需要了解和学习其他空间姿态表示方法。
欧拉角
在所有空间姿态表示方法中,欧拉角可以说是最直观的一种。它用三个数描述从一个坐标系到另一个坐标系的变换,每个数分别是绕某一个坐标轴转动的角度。
比如说,对上文的例子,我们可以通过如下变换从{A}转到{B}:

我们可以说,B坐标系相对于A坐标系的欧拉角为(180, -90, 0)。注意到,仅仅是(180, -90, 0)并不能唯一确定一个旋转变换,我们还需要约定两件事情:
第一,我们选取的旋转轴的顺序是(Z, Y, Z)(最后一个轴在例子中没有体现,用X也是可以的);
第二,我们每一次都是采用旋转后的坐标系,而不是原始坐标系。
每次都采用旋转后的坐标系,也就是采用“附着”在物体上随着它旋转的坐标系,所以我们也称之为intrinsic(固有)坐标系;一直采用原始坐标系,也就是采用一个固定的不随物体而动的坐标系,所以我们也称之为extrinsic(外在)坐标系。为了明确这一点,我们的坐标轴顺序可以写作(Z,Y’,Z”)。上面这个例子,如果我们采用的是原始坐标系,那么“绕YA1轴旋转-90度”就会变成“绕YA轴旋转90度”。
理论上来讲,不同的旋转轴顺序以及extrinsic或intrinsic坐标系的选择,可以形成12 X 2 = 24种不同的组合。这12种旋转轴顺序包括 z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y,以及x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z。没有约定好旋转轴顺序和坐标系选择的欧拉角是没有意义的。
欧拉角用到飞行器的控制上非常直观——给飞机附上一个坐标系,Z轴与地面垂直、Y轴指向正前方,那么飞行员想要飞机绕哪个轴转,他只要操作对应的控制器就好了。如下图所示,这个约定俗成的欧拉角,我们常常用Roll-Yaw-Pitch(滚转-偏航-俯仰)来表示。

欧拉角的万向节死锁
欧拉角的这种表示方式确实方便又直观,特别是在使用物体固有参照系时。但在实际应用中,使用固有参照系的欧拉角来表示旋转变换,却有一个麻烦的问题,叫“万向节死锁”(Gimbal Lock)。
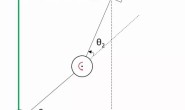
这个死锁问题,在我看来,与常见工业机械臂最后三个旋转关节的奇异点有异曲同工之妙;甚至我们可以利用机械臂来理解欧拉角。通常情况下,三个旋转关节的组合可以任意改变末端执行器的姿态。下图中,(xyz)表示固定不变的外在坐标系,而附着在end effector上的(xi, yi, zi)则表示其固有坐标系。稍微思考一下我们可以发现,这个机械臂从下往上三个关节的转角 (θ1, θ2, θ3),不正代表了按照(Z,X’, Y”)顺序的欧拉角描述的end effector orientation吗?

如果你理解了上面这句话,并且之前认真看过关于雅可比矩阵的几篇文章(链接在此:上篇,中篇,下篇),那么理解欧拉角万向节死锁问题就简单多了,因为这个死锁正是出现在这个三轴机械臂的奇异点上。复习一下之前学过的求雅可比矩阵Jw(这里我们只关心空间朝向,不关心位置)的方法,我们可以得到

求特征值为0的解,可以得到这个机械臂的奇异点在θ2=90°(或-90°)处,这是一个什么情形呢?

我们发现,在第二个关节转了90度之后,第三个关节不管怎么转,其实和第一个关节的转轴是一样的!这个end effector在此刻失去了绕外在坐标的y轴旋转的能力。图上只画了θ1为0°的情况,但很容易想象,不管θ1是多少,只要θ2=+/- 90°,这样的情况都必然发生。
欧拉角的万向节死锁,正是在第二个关节为90度(或-90度)时出现的。此时,物体固有坐标系上的欧拉角最后一个旋转轴,与欧拉角第一个旋转轴正好重合;原本可以表示三个自由度的欧拉角变成了只有两个自由度。
在逆运动学的下篇中,我们采用雅可比矩阵求逆的方法,发现当机械臂到奇异点(附近)时,end effector上很小的姿态变化竟然会导致接近无限大的关节速度,如下图中,处于奇异点的end effector明明没有怎么动,机械臂的关节却非要转个180度。

类似的道理用在采用欧拉角描述姿态的仿真动画(Animation)中,我们就会发现当两个关键帧的运动姿态的改变经过欧拉角的奇异点时,仿真物体的运动也会变得很奇怪(它具体会怎么怪法,可能取决于计算关键帧插值的软件所用的算法)。比如,你理想中它应该是这样的:

实际上它却是这样的:

还有像下图这种,明明我们需要的只是这个物体向左倒下一点(绕垂直于屏幕的轴转动),却因为此时我们用来表示物体空间姿态的欧拉角处于万向节死锁状态,“失去”了这个方向的转轴,而只好歪一歪扭一扭地倒下。

这里也可以看出,欧拉角的万向节死锁并不是一个真正的物理意义上的锁,只是由于我们选取的空间姿态表示方式不够好,而遇到的一个数学意义上的“锁”。
欧拉角的这个麻烦之处,是所有采用三个维度来描述空间姿态的方法都无法避免的。所幸,数学家发明出了四元数(Quaternion)的概念,用四维向量来描述物体在三维空间的姿态以及姿态变化,就这样完美地解决了奇异点的问题,用起来也极其方便。鉴于把四元数这个东西讲清楚需要不小的篇幅,我们在下篇中再一起来探讨。
参考资料
https://en.wikipedia.org/wiki/Rotation_formalisms_in_three_dimensions
https://en.wikipedia.org/wiki/Euler_angles
http://howthingsfly.si.edu/flight-dynamics/roll-pitch-and-yaw
http://fliponline.blogspot.com/2007/04/quick-trick-gimbal-lock-just-ignore-it.html