1. 引言
1.1 闲话
前面一系列博客基本介绍完了机器人正运动学相关的内容,因为后续可能需要在正运动学部分补充代码,案例等。因此从动力学开始的内容将重新编号。 机器人动力学不缺少科普文章,我想当你搜索这个关键词的时候一定是希望了解机器人动力学的本质以及书本上讲述的那一大堆公式到底是怎么来的。因此这一部分内容对于复杂公式推导的态度是剖析而非回避。你将看到大量的数学公式,但是我将力求让每一个具备高中物理知识、基本的微积分知识以及基本的线性代数知识的读者真正看懂这些公式。老实说这对我来说是一个巨大的挑战,因此行文中有什么问题希望各位读者指正。
1.2 关于数学
如果你还是学生以后希望致力于科学工作,我建议你学好大学开的每一门数学课,因为后面你很难再有机会这么系统地学习数学知识。在机器人动力学中充斥着微积分,线性代数的理论,想要理解机器人动力学这些基础知识绕不开。
1.3 关于物理学
机器人动力学应用到的物理学主要是牛顿三大定律,由于机器人本身是一个多刚体系统,因此高中物理需要作相应的扩充(就是大学物理了,幸运的是我们并不需要大物的全部知识体系)。 总的来说我觉得想要真正弄明白机器人动力学这两部分基础知识必须要提前过一遍,不然就是雾里看花。接下来将首先介绍数学基础。
2. 迹
迹是线性代数中的一个概念, 一个方阵的对角线元素之和称为是迹 。对于如下方阵A:
A=\begin{pmatrix} a_{11} & a_{12} & a_{13} & \dots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \dots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \dots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & a_{n4} & \dots & a_{nn} \end{pmatrix}
A的迹为:
trace(A) =a_{11}+a_{22}+\dots+a_{nn}= \sum_{i=1}^{n}a_{ii}
如果你刚开始接触迹这个概念可能会摸不着头脑,因为从定义上看实在太简单了。事实上迹是方阵一个非常重要的特征:
- 相似矩阵的迹相同(有人把迹形象地比作是相似变换留下的痕迹)
- 迹是矩阵的特征值之和
这两个事实抛出来之后迹这个概念一下子就复杂起来了,但是这里我们不详细讨论它的诸多解读,只使用最简单的定义即对角线元素之和。如果你对迹感兴趣可以读一下知乎上这篇帖子的回答。
3. 矩阵的内积
你可能听说过向量的内积,设有两个向量a=\begin{pmatrix} a_1 & a_2 & \dots & a_n \end{pmatrix}^T和b=\begin{pmatrix} b_1 & b_2 & \dots & b_n \end{pmatrix}^T,那么根据内积的定义,向量a和b的内积为:
\left < a, b \right >= a^Tb=a_1b_1+a_2b_2+\dots+a_nb_n=\sum_{i=1}^{n}a_ib_i
因此从形式上看, 两个向量的内积就是对应元素相乘再相加(代数定义)。你可能还看到过这种定义:
\left < a,b\right >=\left |a\right |\left | b \right |cos(\theta)
即 两个向量的内积等于向量模长的乘积再乘上夹角余弦值(几何定义)。这两种定义是等价的。如果你对向量内积的推导过程感兴趣可以参考这篇文章。 那么矩阵内积是个什么呢?矩阵内积其实可以看做是向量内积的延申,他表达的是两个相同大小的矩阵对应元素乘积之和,设有两个均为m行n列的矩阵A和B,他们的定义如下:
A = \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{pmatrix} , B = \begin{pmatrix} b_{11} & b_{12} & \dots & b_{1n} \\ b_{21} & b_{22} & \dots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \dots & b_{mn} \end{pmatrix}
那么矩阵A和B的内积就可以定义为:
\left < A,B\right > = a_{11}b_{11} + a_{12}b_{12}+\dots+a_{mn}b_{mn}=\sum_{i=1}^{m} \sum_{j=1}^{n} a_{ij}b_{ij}
有趣的是我们可以借助前面迹的概念简化矩阵内积的表达形式,矩阵A和B的内积还可以表达为:
\left < A,B\right >=trace(A^T B)
希望你看到这个公式不要奇怪,看起来很复杂,其实很简单,举个二维方阵的例子来理解一下这个公式。设A和B是两个二维方阵(只要矩阵尺寸相同即可计算其内积,不一定是方阵),表达为:
A=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}, B=\begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix}
那么根据内积的原始定义,这两个矩阵的内积应该是:
\left < A,B\right > = a_{11}b_{11} + a_{12}b_{12}+a_{21}b_{21}+a_{22}b_{22}
再来分析一下含有迹运算的这个公式:
A^T B= \begin{pmatrix} a_{11}b_{11}+a_{21}b_{21} & a_{11}b_{12}+a_{21}b_{22} \\ a_{12}b_{11}+a_{22}b_{21} & a_{12}b_{12} + a_{22}b_{22} \end{pmatrix}
求上面A^T B的迹你会发现结果正好是符合矩阵内积的原始定义的。
4. 导数与微分
导数与微分无论从形式上还是从物理意义上都存在一定的相似性,因此很多人包括作者在内都经常将两者视为同一个概念,这通常不会有问题。但是如果你习惯性地将微分如dx视为无穷小量并进行分子分母相消操作时经常会得到错误的结果特别是在矩阵求导中这种情况会经常发生。究其原因还是因为我们对于微积分的理解还停留在古典微积分。
4.1 古典微积分
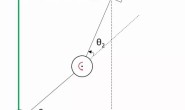
古典微积分是建立在无穷小量基础上的。在十七世纪由牛顿和莱布尼兹分别独立归纳出了古典微积分。这里说归纳还是比较严谨的,因为在此之前微积分的大量知识已经积累起来了(关于微积分的发展历史可以参考这篇文章)。 促使微积分出现的场景非常多,其中一个就是解决复杂曲线下的面积问题。如下图1所示是一条连续曲线。那么如何求解曲线下的面积呢?古典微积分的做法是将这个不规则形状的面积分割为无数多个小矩形的面积之和。
 图1. 曲线的线下面积
图1. 曲线的线下面积可以看到划分的越细致,\Delta x就会越小,最终求解的面积也会越精确。当小矩形的个数趋于无穷多个时,\Delta x将趋近于0,此时用dx来表示\Delta x,代表\Delta x \rightarrow 0。此时的dx就是古典微积分中微分(字面理解为微小的部分)的概念。 在古典微积分中导数的概念也非常直观,它是利用切线去定义的。如下图2所示。
 图2. 从割线到切线
图2. 从割线到切线直线ab分割某一条曲线,交点为a和b,对于割线可以求出它的斜率为:
k=\frac{\Delta y}{\Delta x}
当b点沿着曲线逐渐逼近a点时,\Delta y变成了y的微分dy,\Delta x变成了变量x的微分dx,割线变成了切线。切线斜率此时就称为导数,即:
f’(x)=\frac{dy}{dx}
以上基本就是古典微积分中关于微分和导数的阐述,总的来说非常直观且容易接受,但是却存在着重大的缺陷就是所谓幽灵般的无穷小量。这个无穷小有的时候会被当做0舍弃掉,有的时候又去参与分子分母相消的运算,搞得很无厘头。数学的严谨性是不允许存在这样的瑕疵的。所以才有了后面的基于极限的导数与微分。 总结一下古典微积分中:
- 微分被认为是变量的微小部分
- 导数被认为是曲线切线斜率 很直观,遗憾的是有瑕疵。
4.2 基于极限的微积分
极限概念的引入使得微积分的导出过程更为严谨,所以现在的教科书里大多数都是基于极限建立微积分。基于极限的导数定义如下:
f’(x) = \lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x \rightarrow 0}{\frac{f(x+\Delta x) – f(x)}{\Delta x}}
由导数的定义,我们可以基于严格的数学推导导出微分的定义。根据上式移项可得:
\lim_{\Delta x \rightarrow 0}\left (\frac{\Delta y}{\Delta x} – f’(x) \right) = 0
此时可以令:
\frac{\Delta y}{\Delta x} – f’(x) = \sigma
那么:
\Delta y = f’(x) \Delta x + \sigma \Delta x
由于\sigma的存在上式是一个严格的等式。此时令:
dy = f’(x)\Delta x
举个特例,如果y=f(x)=x(我们推导的是一个普遍性的概念即微分,因此它应该适用于所有的连续函数,自然会包括y=x这样的简单线性函数),那么上式即为dy=dx=1\Delta x,因此dx和\Delta x在此处是等价的。因此:
dy = f’(x)dx
这就是极限意义下微分的定义,因此在基于极限的微积分中: 1. 导数是一个极限 2. 微分是一个函数 这个过程都是经过严格数学推导得到的,所以会比较抽象,但总的来说还是比较容易理解的。正因为微分本身是一个函数,所以才会说\frac{du}{dy}\frac{dy}{dx}这种式子中直接约去dy是十分鲁莽的举动(我们很多时候是这样做的,但是有些时候这样做是错误的,在极限框架下这个相消操作是需要证明才能进行的)。
5. 总结
这篇文章介绍了几个基本的数学概念,总的来看没有超出微积分和线性代数的范畴。下一篇文章将基于本文内容探讨一种在动力学中非常关键的运算即矩阵导数。由于个人能力有限,所述内容难免存在疏漏,欢迎指出,欢迎讨论。
6. 参考文献
[1]. 迹的几何意义是什么? [2]. 矩阵的迹(Tr) [3]. 数学——向量点积公式推导 [4]. 微分和导数的关系是什么?两者的几何意义有什么不同?为什么要定义微分 ? [5]. 导数与微分到底有什么区别? [6]. 微积分发展史 [7]. 微积分从古至今的完整发展历程