1. 引言

前面的两篇文章分别利用几何方法和解析方法推导了机器人的雅克比矩阵，我想到目前为止你对雅克比矩阵应该有了一个大体的认识，最朴素的理解，雅克比矩阵可以利用机器人关节角速度求解末端执行器的笛卡尔空间速度和角速度。但是在实际应用中经常会出现已知末端执行器的笛卡尔空间速度和角速度，求解机器人关节角速度。这个时候就牵扯到矩阵求逆的问题。这篇文章主要介绍雅克比矩阵的伪逆计算。

2. 广义逆（Generalized inverse）

我们先用一个实际问题引入广义逆这个概念。假设在一个机器人控制任务中，已知末端执行器笛卡尔空间速度（线速度和角速度）为，已知机器人当前的关节角度（n代表关节数量），现在想要求解机器人各个关节的角速度，要怎么办呢？从前面两篇对雅克比矩阵的介绍你应该了解到上述变量存在以下等式所描述的关系。

(1)

如果雅克比矩阵是方阵并且可逆，你应该很容易就能求解关节角速度。

(2)

然而事情总是不像想象中那么顺利，实际情况一是雅克比矩阵可能不是方阵，二是雅克比矩阵即使是方阵也可能不可逆，这个时候要怎么办呢？广义逆可以帮助你解决第一个问题，这也就是为什么我们需要广义逆。

2.1 广义逆的定义

维基百科中针对广义逆有这样的描述：广义逆又称伪逆（以下将混用两个概念），它具有部分逆矩阵的特性。数学上的定义是假设一个矩阵以及另一个矩阵，若满足，则即为的广义逆阵。

机器人学中我们经常使用的是一种叫做单边逆矩阵的广义逆（左广义逆或右广义逆），若矩阵的维度是且为满秩，若则用左逆矩阵，若则用右逆矩阵。

左逆矩阵
右逆矩阵

2.2 广义逆的合理性

前面定义了半天你可能会觉得云里雾里，下面我们做几步数学推导来验证一下广义逆的合理性。在此之前还是啰嗦一些线性代数的基础知识。

2.2.1 线性表示与线性无关

我们以二维空间为例来说明这个问题，如下图 2-1所示描述的是二维空间中两个不平行的向量。

15. 机器人正运动学---雅克比矩阵伪逆

图 2-1 不平行的二维向量

你应该不难想象，对于二维空间中任意其他向量均可以用这两个向量和线性表示，即

(3)

这就是所谓线性表示。当向量和是两个平行向量时，他们两个的线性组合肯定还是和这两个向量平行，因此虽然有两个向量，但是他们是线性相关的，也正因为线性相关，这两个向量就不能用于表示二维空间中的任意向量了。此时如果你把两个向量和写成矩阵的形式，你会发现这个矩阵的列秩为1。

扩展一下，如果是有m个n维向量，如果他们中的任何一个都不能用其余向量线性表示，那么我们就认为这m个向量是线性无关的。你应该不难想象，对于n维空间而言，这样的线性无关向量最多有n个。

2.2.2 列空间

前面说了线性表示和线性无关，接下来我们聊一下列空间，所谓列空间就是将矩阵的列向量进行任意形式的线性组合，得到的向量的集合。对于，他的列空间即为:

15. 机器人正运动学---雅克比矩阵伪逆 (4)

如果矩阵各个列向量都是线性无关的，那么矩阵的列一定是满秩的(列秩与线性无关的列向量个数是等价的！)。换句话说的列秩与其列空间的维数是一样的。

还是拿前面的二维空间举例。前面介绍的二维向量，如果两个向量是不平行的，那么他们两个一定线性无关，构成矩阵之后，列秩一定是2，列空间一定是2维的。而当两个向量是平行向量的时候，这两个向量一定线性相关，构成矩阵后，列秩一定是1，列空间一定是1维的。

2.2.3 左伪逆的一种解释

接下来我们解一个m维线性方程组，但是却有n个方程，并且，如式(5)所示。

(5)

其中，也就是说这是一个超定方程组(方程个数大于未知数个数)。这种方程在数据拟合的时候会经常出现。

这个超定方程通常是无解的。因为在这种情况下即使是列满秩的，它的列空间也只有m维，而b是一个n维向量，因此b不一定在的列空间中。这时候就需要一些优化的思路了。

假设已经找到了这样一个最优解，那么这个应该具备怎样的性质呢？我们还是拿二维向量说事。现在假设是一个二维列向量，也就是它只有一列，那么它的列空间一定是一维的，现在在二维空间中任取一个向量b，他们两个的位置关系如下图 2-2所示。

15. 机器人正运动学---雅克比矩阵伪逆

图 2-2 矩阵的列空间与任意二维向量b

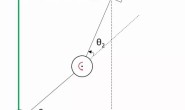
由于矩阵只有一列，因此它的各列线性组合得到的向量其实就是，也就是的列空间实际上就是所在的直线。因此图 2-2向量b不在矩阵的列空间，也就是无解。那么能不能找到一个最优解呢？可以的！只需要让误差取最小值就可以了。虽然向量和b不是垂直的，但是向量可以描述b在上的分量！如下图 2-3所示。此时就是的一个最优解，因为与向量垂直，而垂线段的距离最短（即误差最小）。