本文转载自微信公众号ROBOTICS
各位,机械臂的动力学方程又来和大家见面了!你大概看这个方程看得都生厌了,所幸这也是入门机械臂动力学的最后一篇了——但愿这个方程已经深深地刻在你的脑海里……
神秘的V
不知道大家有没有注意到,上一篇文章中讲到质量矩阵的非对角项时,我在某括号内的文字说“为了暂时先不考虑角速度的影响,我们假设这个瞬间角速度为0”——现在问题来了,如果一个关节角速度不为0,它会对自己以及其他关节的受力产生什么影响呢?
这个问题一时想不清楚没有关系,我们可以采用类似上一篇理解质量矩阵M的路线:从理论推导出的式子出发,反过来理解式子的物理意义。(我们之前怎么 能够在不理解物理意义的情况下就把方程推出来呢?这也算是人的理性思维与数学工具赋予我们的福利啦……)
在动力学第二篇的末尾,我们已经通过拉格朗日方程推导过V的表达式:

这个V看起来不简单,它与质量矩阵对时间的求导、质量矩阵对每个关节的偏导都有关系。对复杂的东西,我们最喜欢用举例子大法,下面我们就再次把上一篇文章中的二自由度机械臂请出来:

我们已经知道它的质量矩阵是:

首先看V表达式的第一项,把M对t求个导:

再把它乘下关节速度得到对应的关节力矩:

你发现没有?这个式子说,要维持两个关节同时匀速运动,第一个旋转关节需要施加一个额外的力矩!这是为什么?
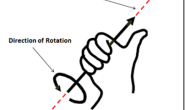
你可能对科里奥利力(Crioris Force、科氏力)非常了解:你知道物体在“旋转参照系”内匀速运动,就会产生一个这样的力;你也发现了这个式子正是科氏力的表达式。不过我相信,如果我们从这个例子出发来讨论,你会对科里奥利力有更清楚的认识。
设想在一个瞬间,第一个关节的角速度为w,第二个关节的速度为v,第二个连杆的质心距第一个关节的距离为d;则此时这个连杆的质心线速度应该是由第一个关节转动造成的线速度wd和由第二个关节运动造成的速度v的向量和。在下一个瞬间,由于d的大小和方向都发生了改变,向量wd(准确地说是w 叉乘 d)的大小和方向、向量v的方向也发生改变,则它的合速度也必然改变。合速度的改变表明加速度不为0,加速度不为0说明为了维持这两个关节的匀速运动,必须有额外的力作用在这个质心。

上面这个图就是前述实验的示意图。对上式进行向量分析可以得到这个额外的力的大小和方向。由于这个力只能由第一个关节提供,所以我们只应该考虑垂直于质心与关节轴的连线的方向。

有了F,只要乘以力矩(d2)就可以得到第一个关节需要施加的力矩——这不正是我们用M矩阵求导所得的结果吗!
我们接着来看V的表达式的第二部分,可以求得

这个式子看起来更熟悉了,这不正是离心力(Centrifugal Force)的表达式吗!它说当第一个关节旋转时,第二根连杆会受到离心力的作用,因此为了维持它的运动状态,第二个关节需要额外施加一个力来补偿。
经过这样一个例子我们发现,神秘的V说来也简单,它分别由科里奥利力和离心力组成,表示了关节的匀速运动对每个关节所需要施加的力矩的影响。
V的另一种形式
上面的例子中,结果正好M对时间求导的一项对应了科里奥利力、M对关节位置求导的一项对应了离心力。实际上稍微复杂一点的情况这一点就不成立了。比如说,上一篇文章中的另一个例子:

只考虑前两个关节,它的质量矩阵为:

现在你可以试着自己求一下V,你会发现M对时间求导的一项求出来是关节二运动产生的离心力在关节一方向上的分量;另外还有一项在两个分量中都出现、然后互相抵消了。

考虑到M对时间的求导实际上就等于M对关节位置的求导乘以关节位置对时间的求导,我们是不是可以用另一种方式写上面的式子,从根源上就把能互相抵消的项去掉呢?
为求方便,我们把M的每一项对关节位置的偏导写成如下形式:

则M的每一项对t的求导可以写为:

现在我们看第i行(也就是有M点q点这一项“贡献”的关节扭矩),可以得到

再看另一项的第i行:

(不知道怎么算的?把向量、矩阵全部展开来写下来就能算了!)
现在把这两项加起来,再整理下:

我们看到,每一个关节所受到的由科里奥利力和离心力贡献的力可以由上式求出:当j=k时,求得的是离心力;否则求得的是科里奥利力。关节速度相乘前的系数可以记为:

原来这就是传说中的克氏符号(Christoffel symbols)……
这样,经过上述运算,我们得到了V乘关节速度向量每一行的表达式;如果再把它写回向量和矩阵的形式,我们可以把V的每一项写成:

甚至我们可以把V按照物理意义拆成两部分:

很明显C是离心力的系数、B是科里奥利力的系数——至于C、B具体是什么样,就留给你自己去写啦。
G
在分析过M和V以后,G对你来说应该是没什么难度了。从拉格朗日方程我们知道,G是系统势能对关节位置的偏导,假设系统的势能只有重力势能,我们可以直接把系统的重力势能V(不好意思这个量也叫V)写出来:

其中向量g是方向竖直向下的重力加速度系数,P(Ci)是第i根连杆的质心的位置向量。
则G项可以由V对关节位置求导得出:

注意这里的g是一个向量,大小为重力加速度的大小,方向竖直向下。我没有写J和g是在哪个坐标系里表示,但和其他所有向量运算一样,我们需要保证它们是在同一个坐标系里。同时注意到这个坐标系定义了重力势能的零势能面,所以我们通常会选基座坐标系frame{0}。
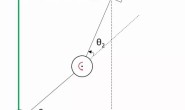
当然,我们从来不满足于仅仅把表达式写出来,我们还要理解它的物理意义——我们的目标是,能用几何大法搞定的决不动手算。比如下面这个机械臂,我就敢直接写:


不难理解:G的每一行正是每个关节需要克服的在它之后所有连杆的重力作用在它身上的分量。
总结
恭喜各位,我们终于把机械臂的动力学方程啃完了。我们看到,动力学方程有着非常明确的物理意义:
等式左边是M+V+G,这是我们的模型,它描述了:
1、机械臂各个关节运动的加速度造成的每个关节所受的惯性力:这个力可以来自于加速自身的关节、也可能来自于其他关节的加速运动的耦合;
2、机械臂各个关节运动的速度对其他关节造成的惯性力,它可能是科里奥利力或离心力;
3、机械臂各个关节需要克服的机械臂自身重力。
等式右边是τ,这将会是我们的控制量,它表示根据我们建立的机械臂动力学模型,要让关节按照既定轨迹(位置、速度、加速度)运动,每个关节驱动器需要施加的力矩。
从期望的机械臂运动位置、速度和加速度计算出每个关节需要施加的力矩,这个过程我们称为逆动力学(inverse dynamics)。
有朋友问到如果机械臂与外界有接触,产生了接触力又怎么算呢?我们通常把它转为等效的关节扭矩,加入等式左侧作为模型的一部分:
![]()
这已经超出了入门的范畴,这里不深入了……
我花很多篇幅讲“物理意义”,是因为我认为物理直觉(physical intuition)是面对像机械臂这样的复杂系统最重要的技能。我们最初都是靠物理直觉来理解这个世界,然后我们总结出了规律、写出了数学方程、再用数学工具解开更复杂的谜题;然而最终,我们还是应该弄明白这些公式究竟在说什么。
希望这两篇关于物理意义的文章是有意义的:)