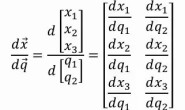干货 | 从RP关节入门机器人学_人工智能

本文转载自微信公众号ROBOTICS

本科阶段的机器人竞赛制作的机器人、生活中见到的扫地机器人，它们都是轮式的移动机器人；移动机器人本身运动控制比较简单，难点在于对外界的感知理解，因此相关研究更多的是人工智能、机器视觉、自然语言处理这一类。然而移动机器人除了移动、简单的搬运货物等功能，缺乏真正的操作（manipulate）外界物体的能力；对这种能力的需求，就是机械臂存在的意义，也是我们学习它的意义。 狭义的机器人学，其基础研究对象是链式(chain)机器人，它们最基本的组成部分，就是关节(Joint)和连杆(Link)。连杆是连接不同关节的机械结构；链式机器人，就是可以用关节-连杆-关节-连杆-……-末端执行机构(end effector)这样的公式表达其结构的机器人。除了链式，还会有树状（如人形机器人，humanoiid robot）、环状机器人（如平行机器人，parallel robot）。

基础关节

RP关节是组成机械臂/机器人的基础，R是旋转关节（Revolute Joint），P是平移关节（Prismatic Joint）。请注意，基础关节肯定是只有一个自由度(Degree of freedom/DOF)的，旋转关节只绕某一个轴旋转，平移关节只在某一条直线上运动。因为更高维度的关节（比如有三个自由度的球形关节，Spherical Joint）一定可以由多个基础关节表示。现在可以来看看（上一篇文章被鄙视的）PPP笛卡尔坐标机器人：

干货 | 从RP关节入门机器人学无论它长怎样，你都可以清楚地看到它有三个空间上互相垂直的平移关节，正如最常用的笛卡尔坐标系。这种情况下，我们说这个机器人有三个关节，是三轴机器人，关节空间(joint space)有三个自由度，end effector的操作空间(operational space)同样有三个平动（位置）自由度。joint space和operational space是机器人学非常重要的概念：joint space用来描述每个关节的位置（P关节）或角度（R关节）；operational space用来描述end effector的位置(position)和朝向(orientation)。举例来说，如果你需要end effector沿着空间某一条直线走，那么你需要使用operational space来描述；而如果你需要机器人每一个关节都按照你计算好的角度/位置运动，那么你需要用joint space来描述。现在再回头看看我们之前提到过的SCARA机器人（结构为RRPR）：可以很明显地看出，P关节是唯一能让end effector在竖直方向移动的关节，剩下的三个旋转关节，前两个可以确定end effector在水平面上的位置，最后一个再调整方向……笛卡尔和SCARA机器人，都属于joint space和operational space的映射关系比较简单的机器人；对于复杂一些的机器人，比如后面会出现的由6个R关节组成的PUMA，它们的关系就不是这么简单了。顺便提一下，空间中的自由刚体有六个自由度，三个平动、三个转动。

结构图

为了更直观地表明机器人的结构，不知道谁发明了两类关节符号，画出了如题图那样的机械臂结构图。图中圆形表示的R关节旋转轴垂直于屏幕。P关节却没有垂直屏幕的表示方法——发明人很任性地说，除了PPP，谁需要这个，你把机器人转个个儿就都能画了。 冗余自由度(kinematic redundancy) 学会看结构，我们要能来看点有趣的内容了。上一篇文章我们说，人的手臂有七个（基础）关节，你能数出来吗？——别看手机了，现在动动你的肩膀、你的手肘、你的手腕，数一数它们都有几个基础关节？人体的手臂结构图如下所示（耸肩可能可以算一个P关节，可是人极少用它来完成什么操作，因此忽略不计）：只是为了更直观地表现头和手在哪里而已…… 我们前面说，空间刚体有六个自由度，PPP的joint space有3个自由度，operational space也有3个自由度；SCARA的joint space有4个自由度，operational space也有4个自由度；那么这里，人手臂的joint space有7个自由度，operational space有几个自由度呢？——答案是6个，因为operational space是物理空间，在这个空间里刚体不可能有更多的自由度了。不太严谨地说，这种joint space的自由度比operational space多的情况，就可称为冗余自由度(redundancy)。对于冗余自由度最直观的理解，就是你用你的手握紧近处一个固定的东西（这时在你的operational space，你的手的位置和角度都确定了），你的身体也固定不动，这种情况下，你的手臂（手肘）竟然没有卡死还能动！冗余自由度绝对是大自然赋予人类的伟大创造。在机器人界，冗余自由度通常意味着更高的灵活性。许多研究利用机械臂的冗余自由度实现避障(obstacle avoidance)、或避免自己撞到自己(self-collision avoidance)；防止超出关节可运动范围的限制(joint limit)；或防止机械臂进入奇异点(singularity)，关于奇异点，我们下面很快会讲到。然而，虽然人类控制自己的手臂去完成各种任务是一件几乎完全不用经过大脑的事，控制一个有冗余自由度的机械臂却不那么简单。直观上说，当一个机械臂有冗余自由度时，对应同一个end effector position and orientation的joint position（这是逆运动学研究的内容，即inverse kinematics）通常有无数个解；如何解决这个问题，在无数个解中找出最合理的那一个，已经是机器人学高级阶段才会学习到的内容。最后还要说，冗余自由度其实是一个相对的概念。更确切地说，是一个joint space相对于任务空间(task space)的概念。那什么是task space呢？顾名思义，如果你的任务是要在一个平面内定位，那么你的任务空间就需要两个自由度；如果你的任务是要在三维世界中确定朝向，那么你的任务空间就需要三个自由度。严谨地说，当可用于完成任务的关节空间自由度大于任务空间自由度时，我们就称之为redundancy。

奇异点(singularity)

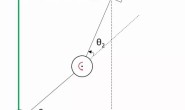
我们前面提到redundancy可以用来避免进入奇异点，奇异点是什么，又为什么需要避免呢？试试看，当你伸直手臂、并把你的手臂和桌子边缘一条直线重合时，若保持身体不动，你能让你的手沿着这条直线前进或后退吗？我们前面说，人的手（即人手臂的end effector）是具有全部6个自由度的，为什么在这个时候，它在与手臂平行的方向完全无法运动了呢？像这种机械臂的end effector失去了某个方向的自由度，在该方向上运动速度只能为0、该方向上的力/扭矩全完全由机械结构承担（而不需要关节上的电机/肌肉等actuator出力）的情况，就称为kinematic singularity。除了伸直手臂这一个singularity（我们称为elbow lock，肘部奇点），机械臂的世界还有很多singularity的情况。比如很经典的wrist lock（腕部奇点），工业上通常称为第4-第6轴平行产生奇异点（如果你看第二张图一个经典工业机械臂PUMA的示意图，里面也出现了wrist lock，正是由第4-第6轴平行产生），此时end effector失去了在垂直屏幕方向运动的自由度。再比如overhead lock（顶置奇点）, 通常是当第4关节位置与第1关节旋转轴重合时产生，此时end effector同样只能在屏幕面上运动，无法在垂直屏幕的方向运动；你可以把手举高让手腕与肩膀在同一直线上，然后试着在垂直手臂平面的方向移动手腕感受一下。在机械臂的线性代数世界里，redundancy意味着线性方程有无数个解，而singularity则意味着某个矩阵（雅可比矩阵）的降秩（从而不可逆、线性方程无解）。更重要的是，当机器人接近singularity时，这个矩阵也越来越接近不可逆，此时由operational space的速度来计算joint space的速度，可能会得到接近无限大的计算结果；这种情况对于机器人来说，当然是非常危险。以上讲的所有东西都只是为了建立直观印象，窥探机器人学里的趣味与难题。要真正学好机器人学，最终还得从线性代数的角度去理解。从下一篇标明干货的文章开始，我们要拿起线性代数这个工具，从坐标变换开始，到描述机器人关节和连杆关系的DH参数，到正运动学(forward kinematics)、逆运动学(inverse kinematics)和动力学(dynamics)；走进机器人学的数学世界，才算真正走进了机器人学。这篇文章介绍了一些重要概念：