3. Minimum Snap轨迹规划
轨迹规划的目的:求轨迹的多项式参数p1,...,pk。 我们可能希望轨迹满足一系列的约束条件,比如:希望设定起点和终点的位置、速度或加速度,希望相邻轨迹连接处平滑(位置连续、速度连续等),希望轨迹经过某些路径点,设定最大速度、最大加速度等,甚至是希望轨迹在规定空间内(Obstruction check)等等。 通常满足约束条件的轨迹有无数条,而实际问题中,往往需要一条特定的轨迹,所以又需要构建一个最优的函数,在可行的轨迹中找出“最优”的那条特定的轨迹。 所以,我们将问题建模(fomulate)成一个约束优化问题,形如:  这样,就可以通过最优化的方法求解出目标轨迹参数p。注意:这里的轨迹参数p是多端polynomial组成的大参数向量
这样,就可以通过最优化的方法求解出目标轨迹参数p。注意:这里的轨迹参数p是多端polynomial组成的大参数向量
 f(p)函数和Aeq,beq,Aieq,bieq参数给列出来,然后丢到优化器中求解轨迹参数p。
f(p)函数和Aeq,beq,Aieq,bieq参数给列出来,然后丢到优化器中求解轨迹参数p。 
4. 一个简单的例子
给定包含起点终点在内的k+1个二维路径点pt0,pt1,...,ptk,pti=(xi,yi),给定起始速度和加速度为v0,a0,末端加速度为ve,ae,给定时间T,规划出经过所有路径点的平滑轨迹。
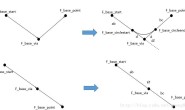
a. 初始轨迹分段与时间分配
根据路径点,将轨迹分为k段,计算每段的距离,按距离平分时间T(匀速时间分配),得到时间序列t0,t1,...,tk。对x,y维度单独规划轨迹。后面只讨论一个维度。 时间分配的方法:匀速分配或梯形分配,假设每段polynomial内速度满足匀速或梯形速度变化,根据每段的距离将总时间T分配到每段。  这里的轨迹分段和时间分配都是初始分配,在迭代算法中,如果 Obstruction check和 feasibility check不满足条件,会插点或增大某一段的时间。
这里的轨迹分段和时间分配都是初始分配,在迭代算法中,如果 Obstruction check和 feasibility check不满足条件,会插点或增大某一段的时间。
b. 构建优化函数
Minimum Snap的优化函数为: 
 其中,
其中,  注意:r,c为矩阵的行索引和列索引,索引从0开始,即第一行 r=0。 可以看到,问题建模成了一个数学上的二次规划(Quadratic Programming,QP)问题。
注意:r,c为矩阵的行索引和列索引,索引从0开始,即第一行 r=0。 可以看到,问题建模成了一个数学上的二次规划(Quadratic Programming,QP)问题。
c. 构建等式约束方程
1.设定某一个点的位置、速度、加速度或者更高为一个特定的值,可以构成一个等式约束。  例如:
例如:  由于要过中间点,对中间点的位置也构建等式约束,方法同上。 2. 相邻段之间的位置、速度、加速度连续可以构成一个等式约束
由于要过中间点,对中间点的位置也构建等式约束,方法同上。 2. 相邻段之间的位置、速度、加速度连续可以构成一个等式约束  例如第i、i+1段的位置连续构成的等式约束为
例如第i、i+1段的位置连续构成的等式约束为  合并所有等式约束,得到
合并所有等式约束,得到  等式约束个数=3(起始PVA)+k-1(中间点的p)+3(终点pva)+3(k-1)(中间点PVA连续)=4k+2。
等式约束个数=3(起始PVA)+k-1(中间点的p)+3(终点pva)+3(k-1)(中间点PVA连续)=4k+2。
d. 构建不等式约束
不等式约束与等式约束类似,也是设置某个点的P、V、A小于某一特定值,从而构建Aieqp=bieq ,不等式约束一般是在corridor中用的比较多,这里暂时先不使用不等式约束。
e. 求解
利用QP求解器进行求解,在MATLAB中可以使用quadprog() 函数,C++的QP求解器如OOQP,也可以自己去网上找。  参考资料: 1、深蓝学院 2、https://blog.csdn.net/q597967420/article/details/76099491
参考资料: 1、深蓝学院 2、https://blog.csdn.net/q597967420/article/details/76099491
 其中p0,p1,...,pn为轨迹参数(n+1个),设参数向量p=[p0,p1,...,pn]T,则轨迹可以写成向量形式。
其中p0,p1,...,pn为轨迹参数(n+1个),设参数向量p=[p0,p1,...,pn]T,则轨迹可以写成向量形式。  对于任意时刻t,可以根据参数计算出轨迹的位置P(osition),速度V(elocity),加速度A(cceleration),jerk,snap等。
对于任意时刻t,可以根据参数计算出轨迹的位置P(osition),速度V(elocity),加速度A(cceleration),jerk,snap等。  一个多项式曲线过于简单,一段复杂的轨迹很难用一个多项式表示,所以将轨迹按时间分成多段,每段各用一条多项式曲线表示,形如:
一个多项式曲线过于简单,一段复杂的轨迹很难用一个多项式表示,所以将轨迹按时间分成多段,每段各用一条多项式曲线表示,形如:  k为轨迹的段数,
k为轨迹的段数,![]() 为第i段轨迹的参数向量。
为第i段轨迹的参数向量。