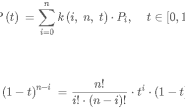本文的内容是对另一篇文章(链接)的补充,对Trajectory_example.cpp涉及到的原理作一些简单的讲解,主要内容是: (1)机器人路径规划圆弧过渡的原理; (2)机器人路径规划梯形波的原理; (3)机器人末端姿态插值的方法(角-轴); (4)KDL使用了pathlength的概念并简述插值的方法。
1 圆弧过渡
机械臂末端从起点A到终点F,中间需要经过若干个中间点(B-E)。首先将所有的点,按顺序用线段连接起来,若两段相邻的线段出现较大的转折,则对两段线段作圆弧过渡。  图1 初步用线段连接
图1 初步用线段连接  图2 圆弧过渡 程序见Path_RoundedComposite::Add(const Frame& F_base_point)
图2 圆弧过渡 程序见Path_RoundedComposite::Add(const Frame& F_base_point)
2梯形波的原理
以一维空间里的位移规划为例,若要使质点从起点到终点满足梯形的速度规律,需要知道的参数为(1)两点之间的位移的距离 ;(2)最大的速度的值 ;(3)加速度的值 ;由于参数选择的差异,可能会出现以下两种波形如图3,一种是完整的梯形波,一种是不完整的梯形波:  图3 两种梯形波
图3 两种梯形波
 式(1) 其中:
式(1) 其中:
 两种情况都可以使用式(1)来对t时刻的位移值进行计算,这也是插值的基础。 程序见:
两种情况都可以使用式(1)来对t时刻的位移值进行计算,这也是插值的基础。 程序见:
void VelocityProfile_Trap::SetProfile(double pos1,double pos2);
和
double VelocityProfile_Trap::Pos(double time) const;
3姿态插值
对位移进行插值比较清晰,对刚体的姿态插值则是难点。KDL使用“角-轴”的方法对刚体的姿态进行插值。 角-轴表示姿态:我们知道,给定两个在笛卡尔空间中具有相同原点不同姿态的起始坐标系和终点坐标系,总可以确定一个单位向量,使得可以通过起始坐标系绕单位向量的轴,旋转一个合适的角度得到终点坐标系。 令Ri 和Rf分别表示起始坐标系和终点坐标系的旋转矩阵,那么这两个坐标系之间的旋转矩阵可以通过(2)式来计算得出:
 如果使用矩阵 (t)来表示Ri到Rf的变换,可得RRt(0)=I, Rt(tf)=R′,矩阵R′表示为绕空间中某一固定轴的旋转矩阵, 当 时,可以使用(3)式和(4)式来计算轴的单位向量rr和旋转角θ。
如果使用矩阵 (t)来表示Ri到Rf的变换,可得RRt(0)=I, Rt(tf)=R′,矩阵R′表示为绕空间中某一固定轴的旋转矩阵, 当 时,可以使用(3)式和(4)式来计算轴的单位向量rr和旋转角θ。
 在求得 θ后即可对其进行插值。 程序见:
在求得 θ后即可对其进行插值。 程序见: Rotation Rotation::Rot2(const Vector& rotvec,double angle) 和
double Rotation::GetRotAngle(Vector& axis,double eps)
4 使用pathlangth对位移和角度同时插值
现在有了位置位移的总长度(或圆弧的弧长)和姿态变换的角度,需要对两者进行插值,插值的核心在于求取长度/角度的位置pos、速度v和加速度a这三者分别与时间的数学关系式,如第2部分所述,有了距离,最大速度和加速度这三个参数,位置/速度/加速度与时间的关系即可生成。很自然地,可以对位移和角度分别求取数学关系式,但是这样会造成位移和角度的速度规律不一样,也就是说,两者无法在同一时刻达到最大的速度。KDL期望实现两者能够同时达到相应的最大的速度,然后保持运行相同的时间,然后在同一时刻都开始减速。 KDL里方法是这样的,它通过一个等效半径将角度与其想乘转化为等效长度,表示姿态的变换的幅度,而质点的位移的路径长度(线段加圆弧长)表示位移的变化的幅度。通过比较出这两者的大小,来确定将谁作为pathlength(程序里的s)。具体的处理方式如下,  图4 KDL里的pathlength和插值 程序见:
图4 KDL里的pathlength和插值 程序见:
Path_Line::Path_Line(const Frame& startpos,
const Frame& endpos,
RotationalInterpolation* _orient,
double _eqradius,
bool _aggregate );
和
Path_Circle::Path_Circle(const Frame& F_base_start,
const Vector& _V_base_center,
const Vector& V_base_p,
const Rotation& R_base_end,
double alpha,
RotationalInterpolation* _orient,
double _eqradius,
bool _aggregate);