Minimum Snap轨迹规划详解（3）闭式求解

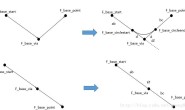
如果QP问题只有等式约束没有不等式约束，那么是可以闭式求解（close form）的。闭式求解效率要快很多，而且只需要用到矩阵运算，不需要QPsolver。 这里介绍Nicholas Roy文章中闭式求解的方法。

1. QP等式约束构建

闭式法中的Q 矩阵计算和之前一样（参照文章一），但约束的形式与之前略为不同，在之前的方法中，等式约束只要构造成[…]p=b的形式就可以了，而闭式法中，每段poly都构造成

其中d₀,d_T为第i段poly的起点和终点的各阶导数组成的向量，比如只考虑PVA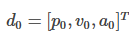：，当然也可以把jerk，snap等加入到向量。注意：这里是不管每段端点的PVA是否

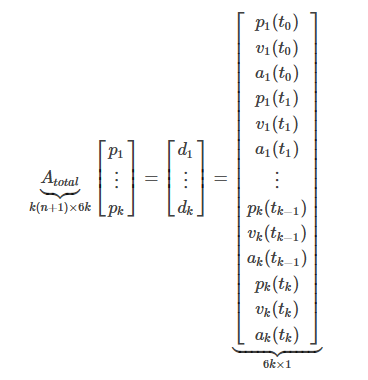
已知，都写进来。 块合并各段轨迹的约束方程得到  k为轨迹段数,n为轨迹的阶数，设只考虑pva，A_total的size为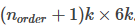。这里为了简化，没有把每段poly的timestamp都改成从0开始，一般，为了避免timestamp太大引起数值问题，每段poly的timestamp都成0开始。 由上式可以看到，A_total是已知的（怎么构造可参见文章一中的等式约束构造方法），而d中只有少部分（起点、终点的pva等）是已知的，其他大部分是未知的。如果能够求出d，那么轨迹参数可以通过p=A^-1d很容易求得。  

2. 如何求d？

  闭式法的思路是：将向量中的变量分成两部分：”d中所有已知量组成的Fix部分d_F”和”所有未知量组成的Free部分d_P”。然后通过推导，根据d_F求得d_P，从而得到d，最后求得p。 下面介绍整个推导过程，  

2.1. 消除重复变量（连续性约束）

  可以会发现，上面构造等式约束时，并没有加入连续性约束，连续性约束并不是直接加到等式约束中。考虑到连续性（这里假设PVA连续），d   向量中很多变量其实重复了，即因此需要一个映射矩阵将一个变量映射到两个重复的变量上，怎么映射？

• 如，将变量a映射到左边向量中的两个变量。   所以构造映射矩阵 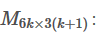       即d=Md’d=Md′。

2.2 向量元素置换

  消除掉重复变量之后，需要调整d’中的变量，把fix部分和free部分分开排列，可以左乘一个置换矩阵C，使得   C矩阵怎么构造？

• 举个例子，设，其中a,b,c是已知(d_F)，b未知(d_p)，构造一个4×4的单位阵，取d_F所在的(1,3,4)列放到左边，再取d_p所在的(2)列放到右边，就构造出置换矩阵C： 

2.3 转成无约束优化问题

  由上面两步可得 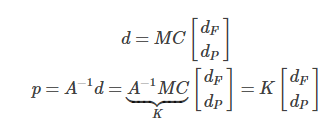  代入优化函数

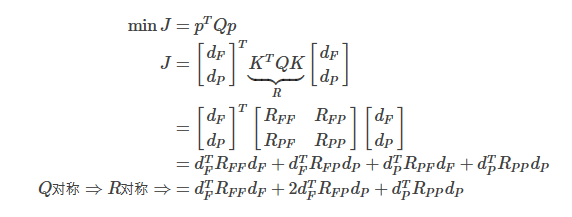
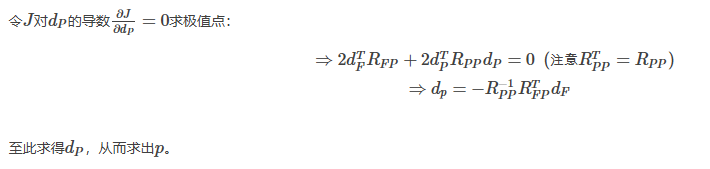
3. 闭式法步骤

  总结一下整个闭式法的步骤：

  1.先确定轨迹阶数（比如5阶），再确定向量中的约束量（pva），进而根据各段的时间分配求得A_{totalAtotal。}

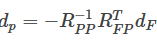　2.根据连续性约束构造映射矩阵M，并确定d向量中哪些量是Fix(比如起点终点pva，中间点的p等)，哪些量是Free，进而构造置换矩阵C，并求得K=A^-1MC^KM=A−1MC 3.计算QP目标函数中的Q（min Jerk/Snap）并计算R=K^TQK，根据fix变量的长度将R拆分成R_FF，R_FP，R_PF，R_PP四块。 4.填入已知变量得到d_F，并根据计算得到d_p 5.根据公式计算得到参数p计算得到轨迹参数p。

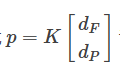计算得到轨迹参数p。=数p。 闭式法主要计算量就在A矩阵的求逆，其他计算基本上是矩阵构造，所以效率比较高，但由于没有不等式约束，所以在中间点只能加强约束，corridor不能直接加到QP问题中，只能是通过压点来实现corridor。 在对计算效率要求比较高或者不想用QPsolver时，可以使用闭式法求解。 代码见这里，由于效果和文章一中的效果一样，这里就不再贴图。 参考链接：https://blog.csdn.net/q597967420/article/details/79031791