开心洋葱 , 版权所有丨如未注明 , 均为原创丨未经授权请勿修改 , 转载请注明仿人型手腕 6R机械臂 D-H参数和运动学逆解!
仿人型手腕 6R机械臂 D-H参数和运动学逆解

-

MATLAB机器人工具箱(二)机器人模型建立 -
8. 机器人正运动学—DH坐标系建立技巧 -

标准DH建模与改进DH建模(一)——标准DH建模方法整理与总结 -
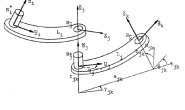
标准DH建模与改进DH建模(三)—— 怎么用改进DH法
- 【关于四足机器人那些事】直驱四足机器人Minitaur运动学建模
- 标准DH建模与改进DH建模
- 机器人动力学与控制学习笔记(二)————机器人动力学建模
- 从网络到分布式-负载均衡
- 潮汐表表v3.0 全新升级
- Error when trying to install SageAttention – distutils._msvccompiler has no attribute ‘_get_vc_env’
- Java 16最前沿技术——ZGC
- 2016年机器人发展五大趋势
- ROS探索总结(一)——ROS简介
- ROS探索总结(二)——ROS总体框架
- ROS探索总结(三)——ROS新手教程
- ROS探索总结(四)——简单的机器人仿真
- ROS探索总结(五)——创建简单的机器人模型smartcar
- ROS探索总结(六)——使用smartcar进行仿真
- ROS探索总结(七)—— smartcar源码上传
- ROS探索总结(八)—— 键盘控制
