二、工业机器人动力学
机器人动力学描述的是关节力矩、动力学参数及关节运动的关系,用于机器人动力学建模的方法很多,如牛顿-欧拉方法、拉格朗日方法、凯恩方法、算子代数方法等。对于同一个机器人,无论采用何种建模方法,最终得到的动力学模型都是等价的,可以表示为:
(2-1)
其中为惯性项,
为科氏力及离心力项,
为重力项,每一项都是机器人惯性参数与关节运动参数的函数。机器人的10个惯性参数可表示为向量的形式:
,其中,参数
为机器人惯量矩阵
中的6个参数,
为
的3个分量(
为质心向量)。上述9个量均包含(2-1)在
及
项内,
表示质量,包含在
项。
基于模型的控制方案主要包括计算力矩控制、动力学前馈控制等,要想通过这些控制方法实现对轨迹的完全精确跟踪,控制方法中的动力学模型必须与机器人实际的动态特性相符。而各种典型建模方法所得到的动力学模型(2-1),只是在理想情况下的结果。实际情况中,影响机器人动力学的因素很多,如加工、装配、材料分布不均等引起的偏差;关节弹性引起的变形所带来的运动学参数偏差;关节摩擦引起的摩擦力矩;由传动方案所引起的不同关节间的运动耦合等。这些因素中,很多无法进行精确建模。为了不增加动力学模型的复杂性,理想的动力学建模方法并未完全考虑这些因素的作用,因此所得到的动力学模型(1-2)与实际的机器人动力学特性是有偏差的。动力学模型的偏差映射到控制方案中,就会引起轨迹的跟踪误差。
2.1 动力学参数辨识
完整的动力学参数辨识主要包括动力学建模、动力学模型的线性化(辨识模型),辨识轨迹优化、辨识算法构造、参数采集与处理、试验验证等几个方面。不同辨识方案在建模、线性化、轨迹优化及试验验证方面没有太大区别,区别主要体现在辨识算法和采集方面。
就辨识算法而言,目前已有神经网络辨识,遗传算法辨识,最大似然估计辨识,卡尔曼滤波算法辨识,最小二乘法辨识等。
数据采集的区别主要体现在力矩的采集上,关节运动参数一般都是通过安装在电机上的编码器测得关节转角,再对关节转角进行微分得到角速度、角加速度。而力矩的采集大致分为两类,即力传感器直接测量及通过电机电流间接测量。对于直接测量,需要在几机器人关节安装力传感器,一般选在末端或基座处,一是因为其他关节在装配后没有安装力传感器的空间,另一方面,每个关节都安装测力传感器势必会大大增加辨识成本;间接测量是通过电机电流测测量值简介计算出电机的驱动力矩值,电机电流与驱动力矩满足:
为关节力矩,
为电机转矩常数,
电机驱动电流。不同测量方案对可辨识的参数类型及参数辨识过程有影响,而不同辨识算法仅对辨识精度有影响。
2.2 牛顿-欧拉动力学建模
牛顿-欧拉动力学方法基于两个基本方程,即力平衡方程以及力矩平衡方程,分别为:
表示作用于机械臂质心处的合力,
表示机械臂质心的线加速度,
表示作用于机械臂质心处的合力矩,
表示相对机械臂质心表示的机械臂惯量矩阵,
表示机械臂角的加速度,
表示机械臂角的角速度。
牛顿-欧拉动力学建模方法包括两部分,即正向运动学递推及反向动力学递推:
(1)正向运动学递推
角速度递推:
![]()
角加速度递推:
![]()
线加速度递推:
![]()
质心处线加速度:
![]()
其中,表示第
与第
坐标系间的姿态转换矩阵,
表示第
与第
坐标原点间的距离向量,
表示
关节的轴线方向,
均为关节变量,分别表示关节的角速度和角加速度,其他各符号含义同前,其中左上标代表参数在哪个坐标系表示,右下标表示参数所隶属的机械臂。
(2)反向运动学递推
机械臂质心处的合力:
![]()
机械臂关节处的作用力:
![]()
机械臂质心处的合力矩:
![]()
机械臂关节处的合力矩:
![]()
最后,将作用于关节处的合力矩向
关节轴线方向投影,得到关节
的驱动力矩:
![]()
这样,得到工业机器人的动力学方程,一般可写为标准形式:
![]()
为机器人的驱动力矩向量,满足:
![]()
其中, 表示第
关节的驱动力矩。
称为机械臂的质量矩阵,是一个对称阵:
对角项通过第
关节的角加速度
产生对第
关节力矩
的力矩分量,非对角项
通过第
关节的角加速度
产生对第
关节力矩
的力矩分量。
为科氏力及离心力项,满足:
其中,
,
,
的后两个下标
表示此力矩分量与
关节的速度有关,他们的动态力相互作用在关节
处产生反作用力(力矩),标号
总表示“感受”到速度引起的反作用力(力矩)的关节编号。当
时,
与关节
“感受”到的关节
的角速度产生的离心力有关;而当
时,
与关节
“感受”到的关节
和
的速度产生的科氏力有关。
2.3 牛顿-欧拉动力学编程
利用Newton-Euler方程建立动力学模型,在Matlab中利用m语言编写程序,完成动力学模型正反解验证。
(1)建立牛顿-欧拉方程逆动力学模型。输入是六个关节的期望角度、速度和加速度,输出是六个关节力矩。
(2)建立凯恩方程正动力学模型。输入是上一级的六个关节的力矩,输出是实际期望角度、速度和加速度。
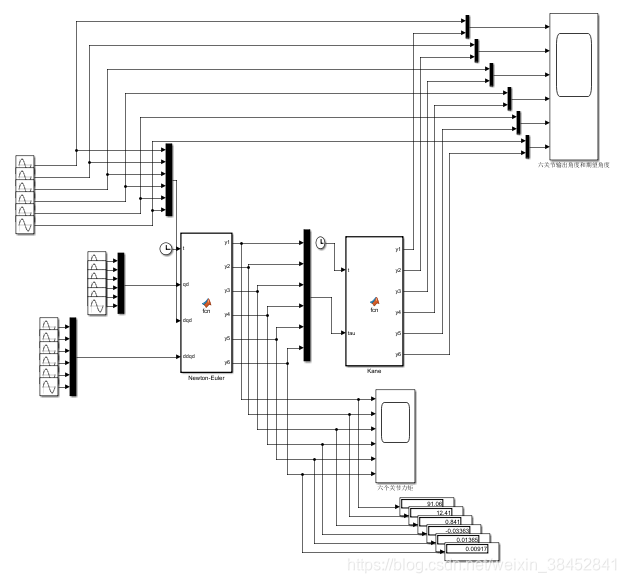
图 1 基于牛顿-欧拉方程和凯恩方程建立的机器人动力学模型simulink仿真图
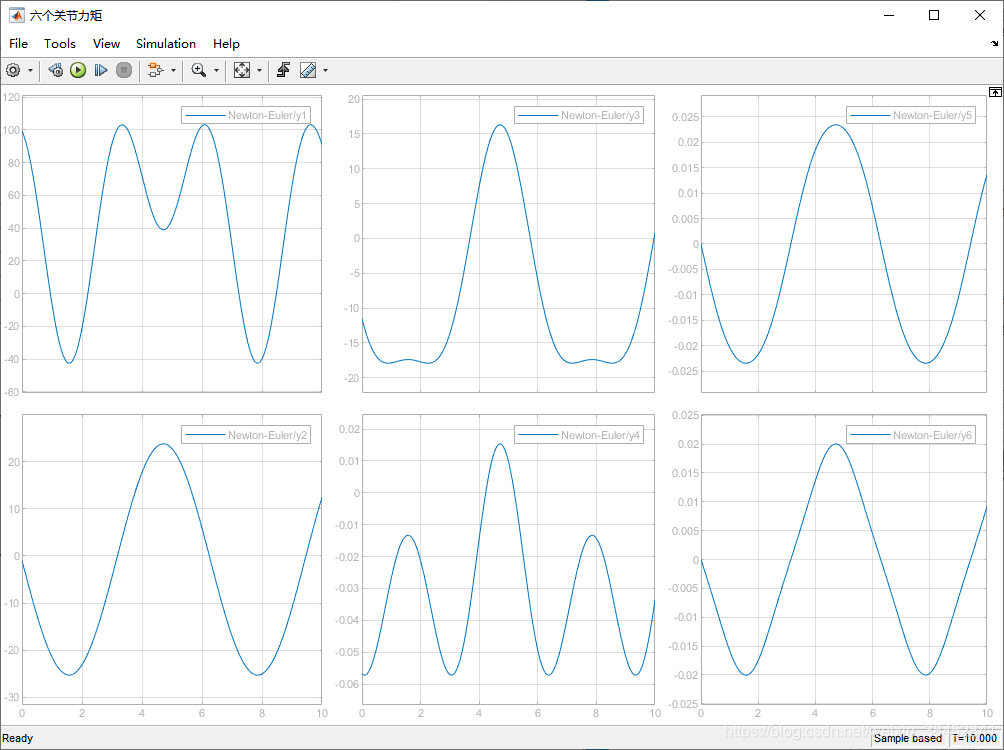
图2 六个关节输出力矩
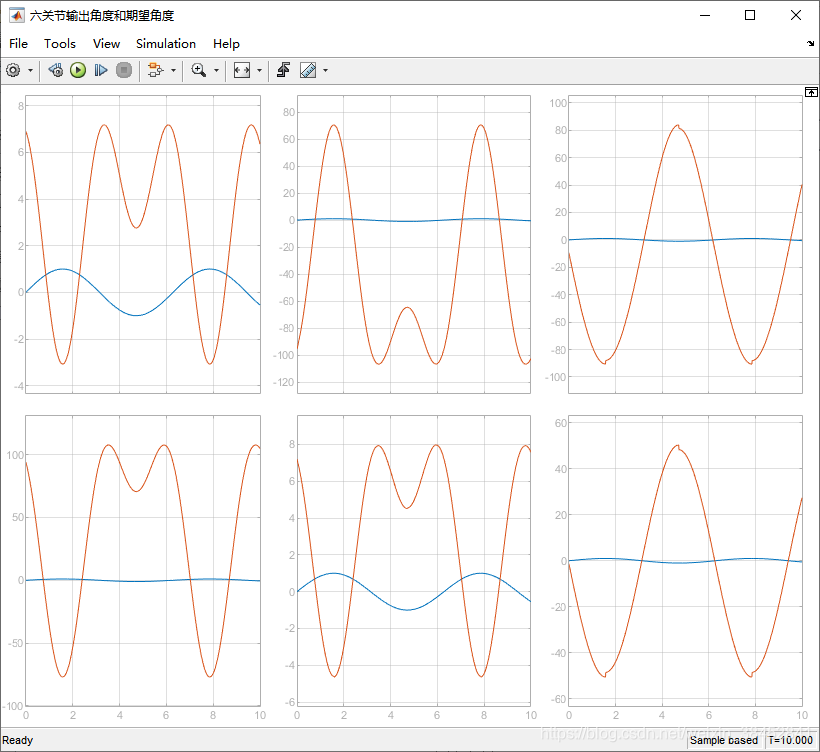
图3 六个关节实际输出角度、速度和加速度