引言
臂形机器人或机械臂是一种我们常见和熟知的机器人类型,机械臂与移动机器人不同,不能再环境中任意移动,有一个固定的基座,因此工作空间有限。非移动的机器人大大简化了诸如感知力和安全性的问题。
机械手的工作对象是空间中的物体,需要机械手手爪按照要求的轨迹和位姿去接近目标物。工业机械臂一般为六自由度,前三个自由度构成的连杆称“主连杆”系统,又称“手臂”,其尺寸较大,用来实现手臂末端的空间位置;后三个自由度的连杆尺寸较小,用来实现机械手末端的姿态,称为“次连杆”系统,又称“手腕”。

串联机械臂的整个链路是由一组连杆刚体组成的,连杆由关节(运动副)连接起来,每个关节有一个平移或者转动的自由度。关节的运动改变了其邻接连杆的相对角度和位置。 Denavit and Hartenberg提出了一种描述串联式链路上连杆和关节几何关系的系统方法,即D-H参数法。

运动学
从连杆坐标系j-1到坐标系j的变换背定义为基本旋转和平移,经过四次变换得到两坐标系的齐次变换矩阵:
代入基本变换矩阵,展开为:
研究机械手各连杆之间的位移关系,进行运动学分析,采用Denavit and Hartenberg参数方法,在每个连杆上固定一个坐标系,用4X4的齐次变换矩阵描述两个连杆的空间位姿关系,从而推导出机械手末端坐标系相对于参考系的等价齐次变换矩阵。
在本文的示例中,三个关节的布置如图所示,肩关节和腕关节在同一平面内,肩关节和肘关节正交
图中Z1、Z2、Z3对应肩关节、肘关节、腕关节传动轴,Z向为关节旋转方向。

采用标准D-H坐标后置法,坐标系固接于连杆的远端,关节轴线为坐标系z轴。得出连杆变换矩阵D-H参数表如下:
在matlab toolbox中的描述代码为:
L(1)=Link([0 0 0.240 -pi/2 0]);
L(2)=Link([0 0 0.240 pi/2 0]);
L(3)=Link([0 0 0.204 0 0]);
shiyanarm=SerialLink(L,'name','实验')

理论推导
机械手末端相对于基础坐标系的变换矩阵为:
机械手末端工具固连与连杆3的末端,工具在坐标系3中的位置齐次矩阵为:
工具坐标和笛卡尔基坐标之间的变化关系为:
我们希望创建一个让机器人跟从的随时间变化的位姿,机械手的末端执行器能沿着既定的位姿轨迹去抓住一个物体。轨迹的一个重要特征是平滑, 通常速度、加速度、加速度率都必须是连续的,常用五次多项式表示光滑的轨迹:
其一阶导数和二阶导数都是光滑的,轨迹及其低阶导数定义了位置、速度、加速度的边界条件,一般速度和加速度边界条件均为0:
理论公式在matlab中的代码求解:
clc;
clear;
syms theta1 theta2 theta3 c1 c2 c3 s1 s2 s3 ;
format long
%连杆固连坐标系后置,标准D-H法
T01=[cos(theta1) 0 -sin(theta1) 0.24*cos(theta1);sin(theta1) 0 cos(theta1) 0.24*sin(theta1);0 -1 0 0;0 0 0 1];
T12=[cos(theta2) 0 sin(theta2) 0.24*cos(theta2);sin(theta2) 0 -cos(theta2) 0.24*sin(theta2);0 1 0 0;0 0 0 1];
T23=[cos(theta3) -sin(theta3) 0 0.204*cos(theta3);sin(theta3) cos(theta3) 0 0.204*sin(theta3);0 0 1 0;0 0 0 1];
T=T01*T12*T23;
T03=vpa(subs(T,{cos(theta1) cos(theta2) cos(theta3) sin(theta1) sin(theta2) sin(theta3)},{c1 c2 c3 s1 s2 s3}))
pf=vpa(T*[0 0 0 1]')
%%雅克比矩阵符号运算解
weizhi=[pf(1);pf(2);pf(3)]
thetaq=[theta1;theta2;theta3]
JJ=jacobian(weizhi,thetaq)
%雅克比矩阵数值解速度椭球
J=subs(JJ,{theta1 theta2 theta3},{pi/4 -pi/4 pi/4})
J=vpa(J)
运动学求解轨迹平滑曲线:
figure(1)
shiyanarm.plot([0 0 0])
figure(2)
plot_ellipse(Jt*Jt')
% 轨迹线图
q2=[-pi/4 -pi/3 pi/4];
init_ang=[0 0 0];
targ_ang=q2;
step=40;
[q,qd,qdd]=jtraj(init_ang,targ_ang,step);
figure(3)
subplot(3,2,[1,3])
shiyanarm.plot(q)
subplot(3,2,2)
i=1:3;
plot(q(:,i))
title('位置')
grid on;
subplot(3,2,4);
i=1:3;
plot(qd(:,i));
title('速度');
grid on;
subplot(3,2,6);
i=1:3;
plot(qdd(:,i));
title('加速度');
grid on;
p1=shiyanarm.fkine(init_ang)
p2=shiyanarm.fkine(targ_ang)
Tc=ctraj(p1,p2,step);
Tjtraj=transl(Tc);
subplot(3,2,5);
plot2(Tjtraj,'r');
title('p1到p2直线轨迹');
grid on;

为了尝试量化描述机器人机构的运动学和动力学性能,提出了机器人可操作性形指标。运动学可操作性是量化机构的速度传递能力,即机构的灵敏性。

描述了位于末端执行器速度空间中的一个六维椭球表面上的点,椭球接近于圆形,则末端执行器可以实现任意的笛卡尔速度。
动力学
机器人的操作臂是一个复杂的动力学系统,存在着严重的非线性,由多个连杆和关节组成,具有多输入和多输出,是一种复杂的耦合关系。为了实现实时控制,利用机器人的动力学模型,才有可能进行最优控制,一起达到最优指标或更好的动态性能。
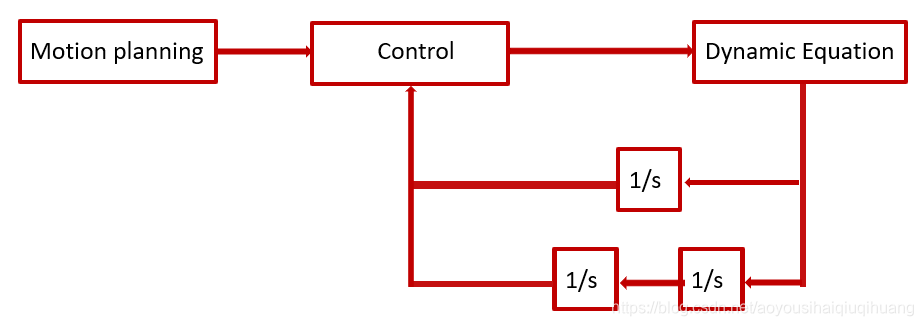
考虑驱动串联机械臂的单个旋转关节的一个电机,电机对外侧连杆施加了一个加速转动的力矩,同时对内侧连杆施加了一个反作用力矩。作用于此连杆到末端连杆的重力也施加到该连杆上,连杆的旋转运动还相互施加了陀螺力。因此,作用在电机上的惯性力是关于所有外侧连杆位姿的一个函数。

该式反映了关节力矩与关节变量、速度与加速度之间的函数关系,H(q)为惯性项,是NxN的正定矩阵;C(q,qdot)离心力和哥氏力矢量,G(q)为重力矢量。F为末端连杆所受外力(Certesian space)。
拉格朗日动力学基于系统能量的概念,对于任何机械系统而言,拉格朗日函数定义为系统的动能和势能之差:
q=[q1,q2,……qn]表示动能和势能的广义坐标,qdot为广义速度。
利用拉格朗日函数,系统的动力学方程为:

利用SolidWorks建立机械臂连杆,计算连杆惯性张量:
Note:由于本文为博主研究生一年级时所作的内容,关于动力学参数的这一部分代码已经丢失,仅剩下ppt中的效果图
肘关节重力载荷

腕关节重力载荷

关节1的惯量随关节2和3的位子变化

关节2的加速度在关节1上的耦合随位姿的变化
reference
[1] Robotics,Vision and Control. Fundamental Algorithms in MATLAB.
[2]霍伟.机器人动力学与控制[M].第一版.高等教育出版社, 2005.





