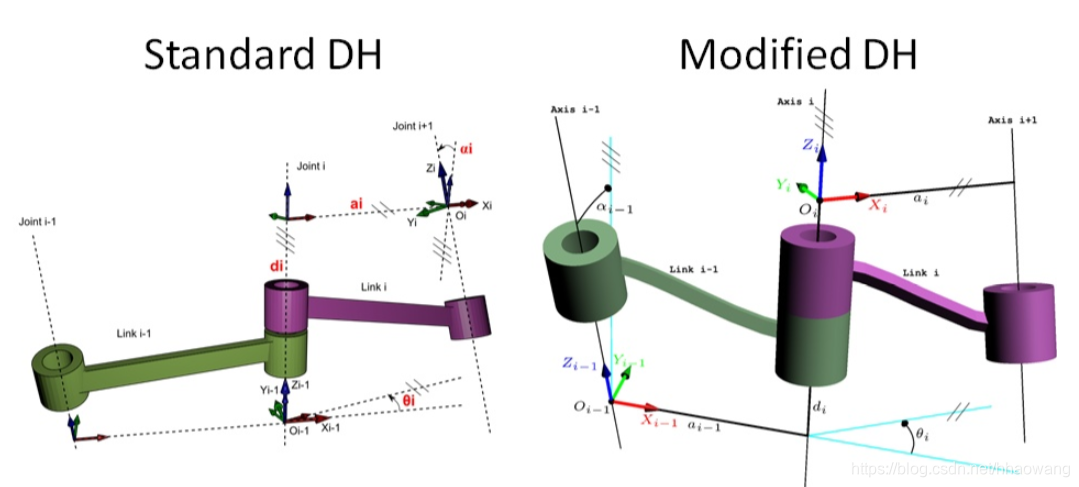
在机械工程中,Denavit-Hartenberg 参数(也称为 DH 参数)是与一个特定约定相关联的四个参数,用于将参考坐标系附加到空间运动链或机器人操作臂的连杆上。
“Jacques Denavit and Richard Hartenberg introduced this convention in 1955 in order to standardize the coordinate frames for spatial linkages”

目录
D-H参数
四个参数定义
D-H矩阵
Modified DH parameters
Matlab D-H法机器人建模
绘图
结果
D-H参数
在机器人技术应用中,一个常用的选择参考框架的惯例是由雅克 · 德纳维特和理查德 · s · 哈滕伯格提出的 Denavit 和哈滕伯格(d-h)公约。在这个惯例中,坐标框架被连接到两个连杆之间的连杆上,这样一个变换与连杆[ z ]相关,而第二个变换与连杆[ x ]相关。由 n 个连杆组成的串联机器人的坐标变换形成了机器人的运动学方程,
![]()
where [T] is the transformation locating the end-link.




四个参数定义
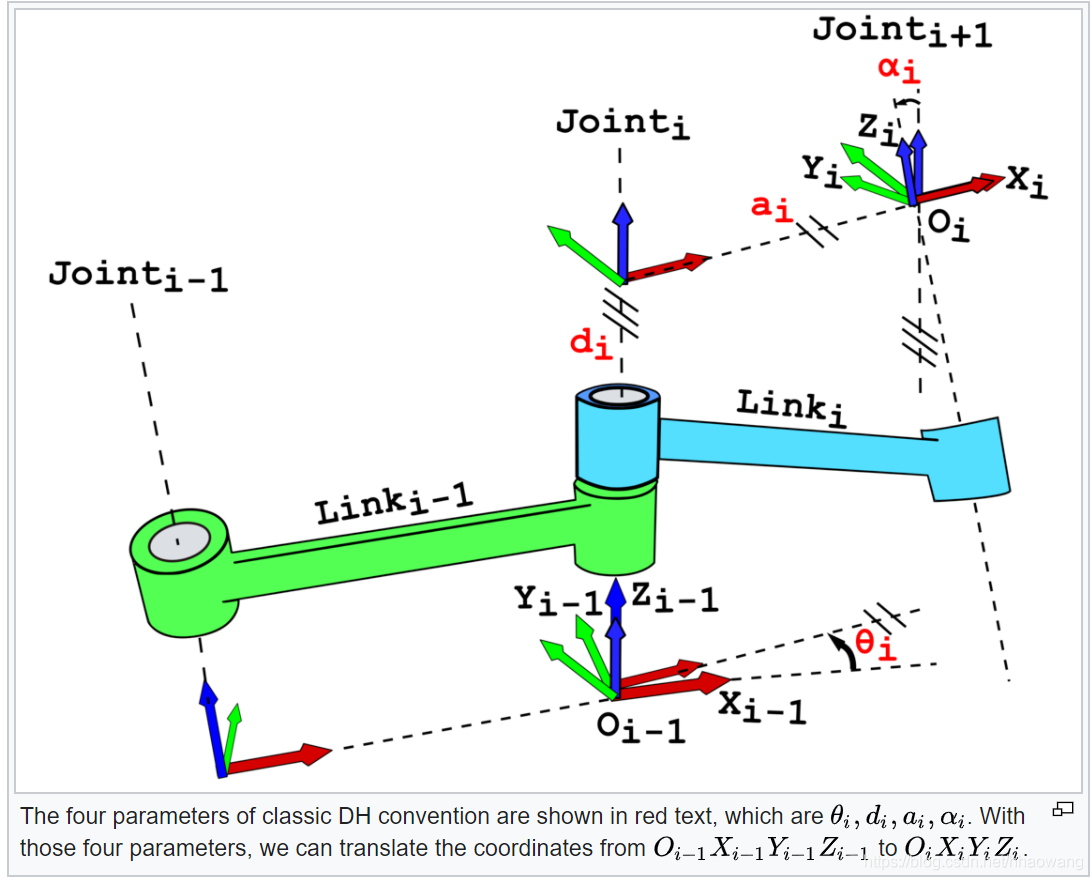

D-H矩阵


Modified DH parameters
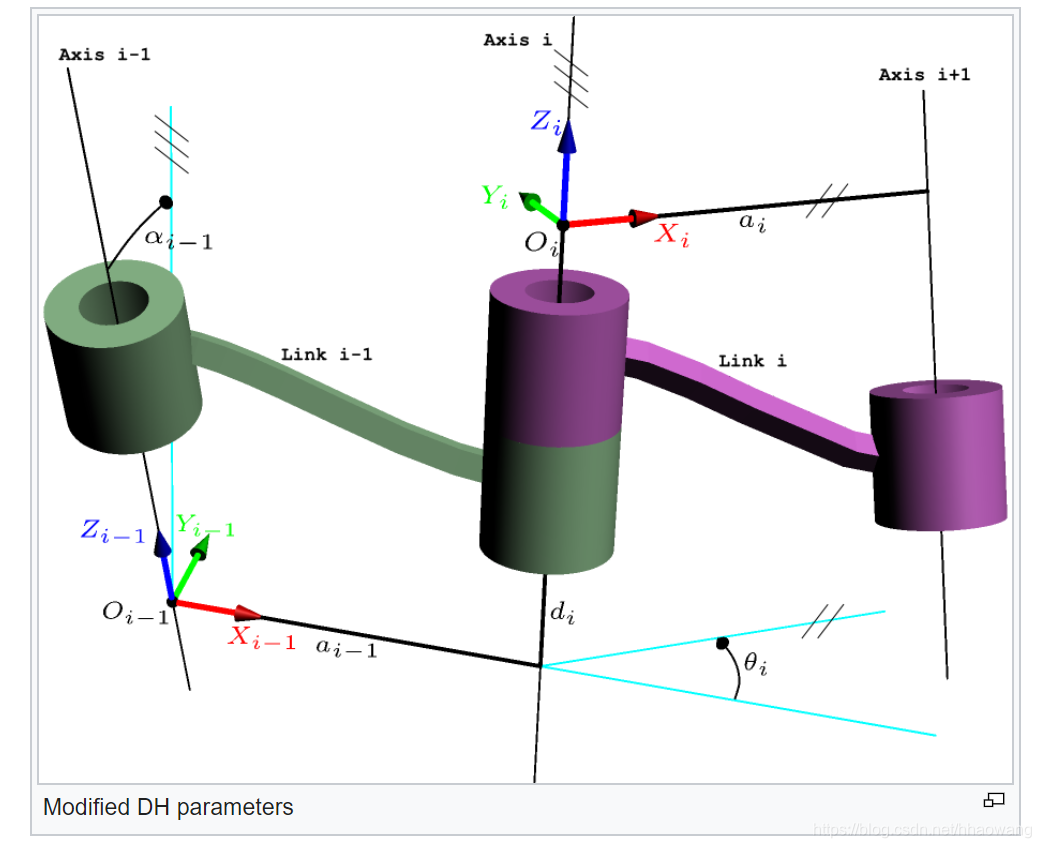

Matlab D-H法机器人建模
MATLAB Robotics Toolbox : https://www.mathworks.com/help/robotics/ug/check-for-environmental-collisions-with-manipulators.html
clear all;
clc;
%Link 类函数
% d_i连杆偏距:ai与ai-1两轴线公垂线之间的距离
% a_i连杆长度:ai-1与ai两关节轴线的公垂线方向上的距离
% alpha_i连杆转角:ai-1与ai两关节轴线投影的夹角
% theta_i关节角:ai关节动角度
L1 = Link('d', 1, 'a', 1, 'alpha', pi/2);
L2 = Link('d', 0, 'a', 1, 'alpha', 0,'offset',pi/2);
L3 = Link('d', 1, 'a', 0, 'alpha', pi/2,'offset',pi/4);
L4 = Link('d', 2, 'a', 0, 'alpha', -pi/2);
L5 = Link('d', 0, 'a', 0, 'alpha', pi/2);
L6 = Link('d', 1, 'a', 0, 'alpha', 0);
b=isrevolute(L1); %Link 类函数
robot=SerialLink([L1,L2,L3,L4,L5,L6]); %SerialLink 类函数
robot.name='带球形腕的拟人臂'; %SerialLink 属性值
robot.display(); %Link 类函数
theta=[0 0 0 0 0 0];
robot.plot(theta); %SerialLink 类函数
theta1=[pi/4,-pi/3,pi/6,pi/4,-pi/3,pi/6];
p0=robot.fkine(theta);
p1=robot.fkine(theta1);
s=robot.A([4 5 6],theta);
cchain=robot.trchain;
q=robot.getpos();
q2=robot.ikine(p1); %逆运动学
j0=robot.jacob0(q2); %雅可比矩阵绘图
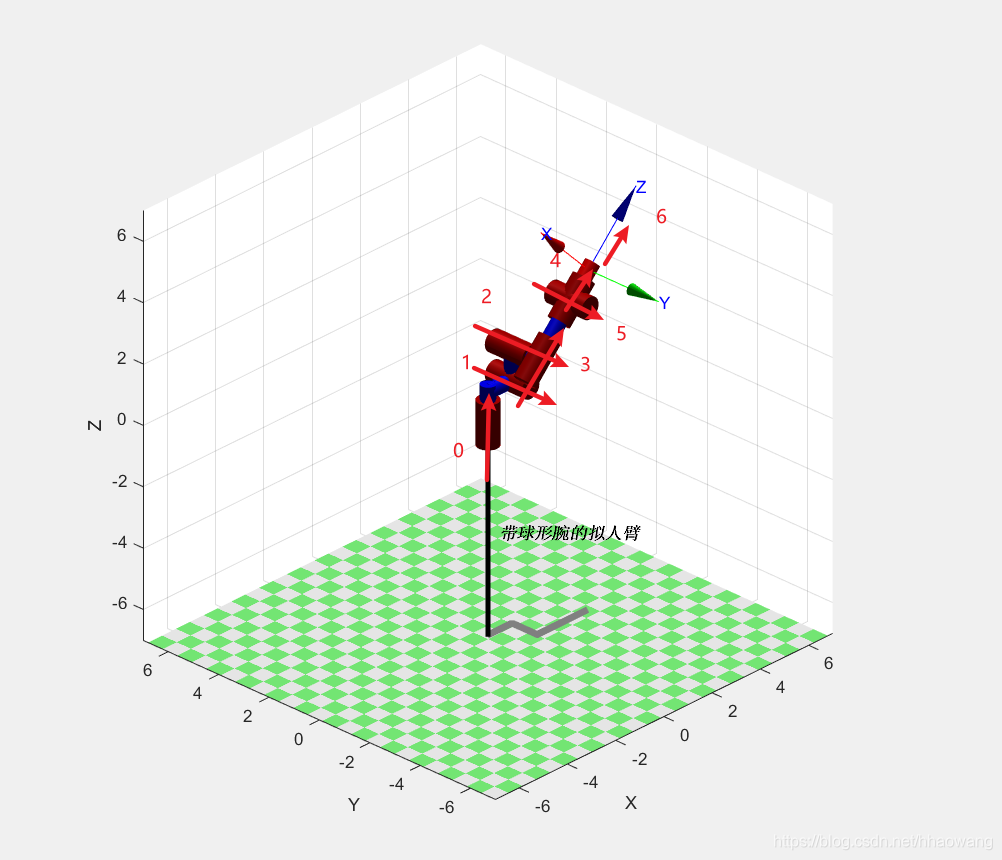
结果



可以看出,逆解和原始的角度并不相同。
机器人工具箱中的比运动学函数并不精确,同时机器人通常有多组逆解,而ikine函数智能求出一组。
对满足pieper条件的机器人,最好自己求出他的解析解,利用解析解来求得多组逆解,不仅速度快,而且更精确。
参考:
Wiki 百科: https://en.wikipedia.org/wiki/Denavit%E2%80%93Hartenberg_parameters
MATLAB D-H : https://blog.csdn.net/xuehuafeiwu123/article/details/52668916