本文转载自微信公众号ROBOTICS
今天,我们终于要开始学习机械臂的动力学了——实话说,上学时候,CC动力学这块真没学懂……
在上一篇干货《运动学好像够用了,我们为什么还需要动力学》中,我们讲了动力学要研究的几个问题、以及研究动力学有什么用。这篇干货意外地比其他干货多了好多阅读量,难道是大家和作者一样对这个问题挺困惑吗?不管怎样,如果你还没看过那一篇,CC建议你去看一看。
刚体动力学(Rigid body dynamics)
我们知道,机械臂是由关节和连杆组成的:关节能够对它所连接的连杆在特定方向施力;连杆则是有质量、有大小(所以惯性张量不可忽略)、不会变形的刚体。由此可见,机械臂动力学的实质就是刚体动力学。
刚体动力学,我们在大学物理应该都学过,但在这篇文章中CC还是会详细地推导一遍。为什么呢?因为把这部分内容仔细地过一遍、清楚透彻地理解它们,对理解更复杂的机械臂动力学问题非常重要。如果你自认对刚体动力学已经非常熟悉,跳过本节也无妨。
刚体动力学研究的是一个刚体的运动状态与它受到的外力的关系。这个关系用欧拉运动定律(Euler‘s laws of motion)即可描述。欧拉运动定律是对牛顿第二定律,即大家熟知的 F = ma 的扩展;如果说牛顿定律描述的是抽象的“物体”或说“粒子”(particle),欧拉定律则将其扩展到无数particle集合到一起组成的具体的有体积的刚体。
欧拉第一运动定律(牛顿定律)
欧拉第一定律描述刚体的线性运动(linear motion)与所受外力的关系。
首先引入线性动量(linear momentum)的概念,它等于一个物体(粒子)的质量乘以线速度。由牛顿第二定律可知(d(mv)/dt = ma = F),线性动量的变化率等于物体所受的外力。
刚体可以看作是无数个particle的集合,刚体的线性动量等于这些particle线性动量的总和。由于刚体的性质,作用在刚体上任意一点的外力等效地作用于所有particle上使它们的线性动量产生变化。于是我们有

等式的右边可以转化为对刚体质量的积分:

其中向量r表示的是在某个参照系中刚体上每一点的位置向量。
注意到质心(center of mass)的定义如下:

(其中下标cm表示center of mass)
于是我们有:

最终,我们得到结论:刚体的线性动量为刚体质量与它的质心线速度的乘积。这个结论表明,在考虑刚体的线性运动时,我们只需要考虑质心的线性运动就够了。
欧拉第一定律说——刚体线性动量的变化率等于它所受到的外力:

显然,线性速度的求导就是线性加速度,所以欧拉第一定律也可以写成以下这个形式。(推导了一大堆,结论和牛顿定律差不多)

欧拉第二运动定律
欧拉第二定律描述刚体的角运动(angular motion)与所受力矩(moment of force)的关系。力矩的概念相信大家都很熟悉了,力作用在particle上,它相对于另一个点O就有一个力臂,力臂与力的叉乘即为力矩。(力矩是一个向量,不是一个标量,方向指向物体旋转的方向。把这个关系记成叉乘,理解上要清晰许多!另外要注意叉乘的顺序)


类似于线性动量,我们也引入角动量(angular momentum)的概念:一个粒子相对于某个定点的角动量等于其质量与角速度的乘积。显然,(相对于这个定点的)角速度等于从定点出发到粒子的位置向量与(相对于这个定点的)粒子线速度的叉乘。
![]()
则角动量写作:
![]()
从牛顿定律F = ma 出发,等式两边用位置向量叉乘可以得到:

于是我们可以得到类似“物体线性动量的变化等于所受外力”的结论:物体角动量的变化率等于它所受到的力矩,即

现在同样的,我们需要把这个结论推广到由无数particle集合而成的刚体上;相对于第一定律的推导,这个部分稍微麻烦一些。
首先我们要推导刚体的角动量表达式,仍然把它看作无数particle的集合,则有

注意到我们把线速度用角速度与位置向量的叉乘代替了,对刚体而言,刚体上每一点的角速度都是相同的,所以我们可以把它取到求和的外面。将上式写作体积分的形式,我们有:

上图中p上面一个小尖称为叉乘操作符(Cross product operator),这个操作符把两个向量的叉乘转换为一个矩阵乘向量的运算。对3×1的向量而言,有

这里,我们把前一张图积分式中括号[]里的部分定义为惯性张量I:

关于惯性张量,篇幅所限我们暂时不详细讨论。最终,我们得到刚体的角动量表达式为

类似力(force)为线性动量的变化率,刚体所受的扭矩(torque)被定义为刚体角动量的变化率。为了求扭矩与角速度、角加速度的关系,我们可以对以上等式两边求导:

dw/dt很显然是刚体的角加速度,dI/dt又是什么呢?它是张量对时间的导数,它不一定等于0!我们知道,张量是刚体上每个点相对于一个静止参照系的位置向量做某些运算之后的体积分,这些位置向量随着刚体的转动而转动;类似于一个点的线速度等于角速度与位置向量的叉乘,我们可以得到:

(非严格推导!只是一种理解方式。)
最终我们得到
![]()
用一张表格总结刚体动力学:

牛顿欧拉法推导机械臂动力学
在花费这么多篇幅详细推导刚体动力学的欧拉运动方程之后,我们终于可以来看看机械臂的动力学了。求解机械臂动力学的最终目的是,如果我们需要控制机器人按照一定的轨迹运动(别忘了轨迹是位置对时间的函数),那么每个关节的驱动器施加多少扭矩(旋转关节)或力(平移关节)。
用牛顿欧拉法推导机械臂的动力学,我们需要两个步骤:首先是“正向传递速度及加速度(forward propagation)”:从基座开始,依次计算每一个连杆的速度、加速度,一直到末端执行器;齐次是“反向传递力(backward propagation)”:从末端执行器所受的外力开始依次算回来求出每个关节的扭矩/力。推导机械臂动力学的牛顿欧拉法是一个递归算法。
Forward propagation
首先看连杆的角速度,每一根连杆的角速度都等于上一根连杆的角速度加上它的关节转动带来的角速度(对平移关节此项为0);根据此我们可以得到连杆角速度的传递公式。公式两边求导,则可以进一步得到角加速度的传递公式。

其中θ是关节位置(旋转关节的角度),Z是关节的转轴。注意上面的式子没有表明每个向量所采用的reference frame,实际计算中,需要利用旋转矩阵把不同参照系的向量映射到同一个参照系中。
对于线速度,每个连杆的线速度等于上一根连杆(质心)的线速度、上一根连杆转动造成的线速度以及平移关节的线速度之和。等式两边求导可以得到线性加速度的传递公式。

其中d是关节位置(平移关节的平移位置),Z是关节平移方向,p是上一个连杆质心到当前连杆的位置向量。
有了速度与加速度的传递公式,我们就可以根据欧拉运动方程方便地求出每个连杆的惯性力和惯性矩:

Backward propagation
现在我们来分析每个连杆的受力情况。由牛顿第三定律可知,力的作用是相互的,所以我们可以用fi来表示每一根连杆受到的上一根连杆的作用力,用ni来表它受到的力矩。

如图所示,我们有

则每个关节的扭矩/力为

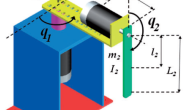
一张图总结这个复杂的过程(针对六自由度的机械臂):

我们的题图则概念化了这个过程:

一个简单的例子
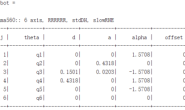
为了大家更好地理解牛顿欧拉递归大法的求解过程(以及更好地了解这个方法有多繁复),这里给大家搬运一个简单的例子——一个只有一个旋转关节的机械臂。

其中,连杆长度为l,质心位置在l/2处。
forward阶段,我们可以求出速度、加速度和惯性力。注意式子中的s1表示sinθ1,c1表示cosθ1,g为重力加速度。





Backward 阶段,我们可以求出

最后我们得到

牛顿欧拉法想法很直观、过程很冗长很复杂——下一篇文章,CC就给大家讲讲少一些简单粗暴、多一些优美智慧的拉格朗日大法。