导言
你也在机器人动力学仿真过程中,遭遇了许多BUG吗?
没关系,在这里或许能找到你想要的答案!
正文
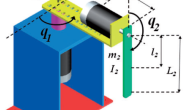
先来考虑一个很简单的情况,假设有一个椭圆形物体放置在水中,其密度与水完全相等,并且通过一个光滑铰链固定,此外,假设水没有阻力。如下图所示:
1 建模
关于这个物体的动力学方程可以列写如下:
其中,θ为旋转角度,ω为角速度,τ为物体所受力矩,J为物体相对于铰链的转动惯量,m为物体质量,g为重力常数,L为铰链到质心的距离。
2 仿真——速度更新放在位置更新后面
Matlab程序如下:
clc;
clear all;
close all;
format long e
%% 参数初始化
T = 10;
period = 0.01;
m = 1;
g = 9.8;
L = 0.01;
J = 0.01;
theta = 0.5;
w = 0;
tau = 0;
Record = [];
%% 开始仿真
for t = 0:period:T
% 计算力矩
tau = -m*g*L*sin(theta);
% 位置更新
theta = theta + period*w;
% 速度更新
w = w + period * tau/J;
% 记录数据
Record = [Record;t, theta, w, tau];
end
%% 绘图
plot(Record(:,1),Record(:,2)*180/pi, 'g',"LineWidth", 3)
xlabel("时间(s)","FontSize", 20)
ylabel("角度(^。)","FontSize", 20)
结果:
3 仿真——速度更新放在位置更新前面
Matlab程序如下:
clc;
clear all;
close all;
format long e
%% 参数初始化
T = 10;
period = 0.01;
m = 1;
g = 9.8;
L = 0.01;
J = 0.01;
theta = 0.5;
w = 0;
tau = 0;
Record = [];
%% 开始仿真
for t = 0:period:T
% 计算力矩
tau = -m*g*L*sin(theta);
% 速度更新
w = w + period * tau/J;
% 位置更新
theta = theta + period*w;
% 记录数据
Record = [Record;t, theta, w, tau];
end
%% 绘图
plot(Record(:,1),Record(:,2)*180/pi, 'g',"LineWidth", 3)
xlabel("时间(s)","FontSize", 20)
ylabel("角度(^。)","FontSize", 20)
结果:
4 结果分析
看完了上面两个仿真结果,我们基于常识可以判断,第2部分中的仿真结果一定是错误的,因为物体并没有外界的能量来源,是不可能震荡得越来越大的。而第3部分的仿真结果就合理多了,由于没有摩擦力,所以物体一直在做等幅震荡。
那么,为什么二者会有这种区别呢?
由于我们控制了变量,只改变了速度更新和位置更新的顺序,因此问题一定出在这个地方。为什么把速度更新放在位置更新的前面,结果才是正确的呢?这个原因我暂时还没有想清楚,如果有读者明白的,可以在博客底下留言谈论。
但是,我发现,这和仿真步长的选择还有一定关系。我发现,即便是把速度更新放在位置更新后面,只要仿真步长足够短,也可以保证结果是正确的。我们可以对比,当仿真步长选为0.1s,0.01s,以及0.001s时的仿真结果。
可以看到,当步长取0.1时,结果就完全不对了,当步长取到0.001时,即便速度更新放在位置更新的后面,仿真结果也和正确结果基本相同。
另外,我们还需要测试,当速度更新放在位置更新的前面时,步长有什么影响?
可以看到,步长几乎没有产生任何影响。
因此,我们可以得出结论,在动力学仿真中,速度更新需要放在位置更新的前面,这样才能保证仿真的正确性。另外,仿真步长应该尽量选短一些,从而保证仿真结果的正确性。
至于,产生这种现象的原因,我知道的是,这应该和仿真过程的数值计算有关系,和仿真步长也有直接关系。如果有热心读者知道是怎么回事的话,欢迎留言讨论。