【机器人学】刚体的惯性张量及其物理意义

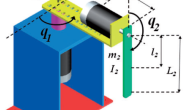
一、刚体的惯性张量   在单自由度系统中，常常要考虑刚体的质量。对于定轴转动的情况，经常用到惯量矩这个概念。对一个可以在三维空间自由运动的刚体来说，可能存在无穷个旋转轴。在一个刚体绕任意轴做旋转运动时，我们需要一种能够表征刚体质量分布的方法。在这里，我们需要引入惯性张量，它可以被看做是对一个物体惯量的广义度量。   现在我们定义一组参量，给出刚体质量在参考坐标系中分布的信息。下图表示一个刚体，坐标系建立在刚体上。惯性张量可以在任何坐标系中定义，但一般在固连于刚体上的坐标系中定义惯性张量。   坐标系{A}中的惯性张量可用3*3矩阵表示如下：  
  矩阵中各元素为：  
  式中刚体由单元体dv组成，单元体密度为ρ，每个单元体的位置由矢量
  二、惯性张量的物理意义   当刚体绕定点转动时，刚体的动量矩为：  
  将上式展开写成矩阵的形式是：  
  右侧3×3矩阵中的求和形式与第一部分中的积分形式是等价的。L i表示刚体绕定点旋转时对每个分坐标轴的动量矩。   参考文献： John Craig 《机器人学导论》 机械工业出版社 2006 洪国维 《惯性张量的物理意义》