本篇将会对四足机器人的腿部进行数学建模,求解器正逆运动学解,包含详细公式推导与计算
一、运动学
不考虑横向髋关节运动时,四足机器人的腿部可以简化成二连杆机构
1、几何建模
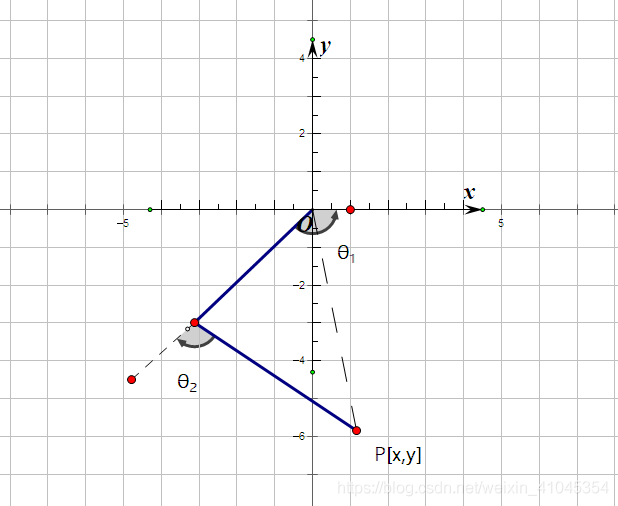
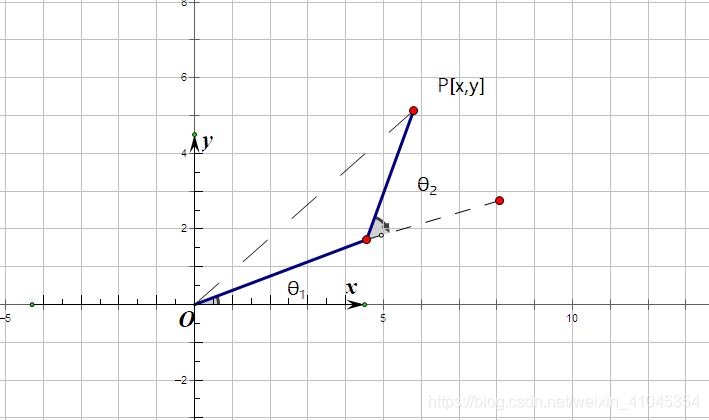
2、运动学正解
如果已知θ1,θ2,可以通过下式求P[x,y]位置: x=L1sinθ1+L2sin(θ1+θ2) y=L1cosθ1+L2cos(θ1+θ2) 如果不明白上面两条公式如何来的,画一条辅助线就能够明白了,如下图:
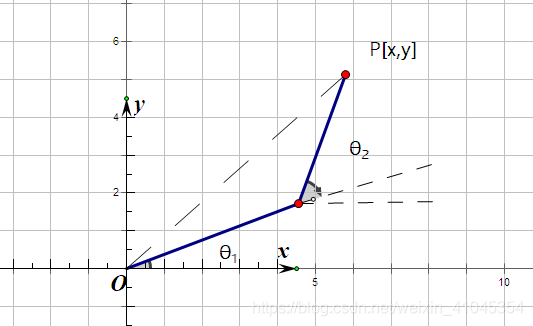
3、逆解
已知P[x,y]位置,求θ1,θ2, 我们用代数的方法求逆解 首先两边平方相加:
 将表达式展开,并写成更简洁的形式,其中cosθ1=c1,cosθ2=c2以此类推:
将表达式展开,并写成更简洁的形式,其中cosθ1=c1,cosθ2=c2以此类推:
 根据和差公式:
根据和差公式:
 或者直接利用python对表达式进行化简
或者直接利用python对表达式进行化简
L1 = symbols('L1')
L2 = symbols('L2')
b = symbols('b')
a = symbols('a')
x = - L1 * sin(a) - L2 * sin(a - b)
y = - L1 * cos(a) - L2 * cos(a - b)
temp = x**2 + y ** 2
result = simplify(temp)
print('x**2 + y ** 2 = ', result)
我们能够得到同样结果
x**2 + y ** 2 = L1**2 + 2*L1*L2*cos(b) + L2**2
求得

这里在求解时需要注意x,y值,验证其是否超过腿部动作空间。
sinθ2有两个取值,会对θ1的值产生影响,在我们当前使用是关节配置方式,sinθ2取正值, 即

接下来我们通过正解来求θ1,先对公式进行以下变换: x=k1s1+k2c1 y=k1c1−k2s1 其中 k1=k2=l1+l2c2 k2=l2s2 再对k1,k2进行变量替换: k1=rcosγ k2=rsinγ 其中
![]() 同样,我们画个图方便理解,k1,k2相当于坐标轴上的点P,γ是r 与x 轴的夹角。
同样,我们画个图方便理解,k1,k2相当于坐标轴上的点P,γ是r 与x 轴的夹角。
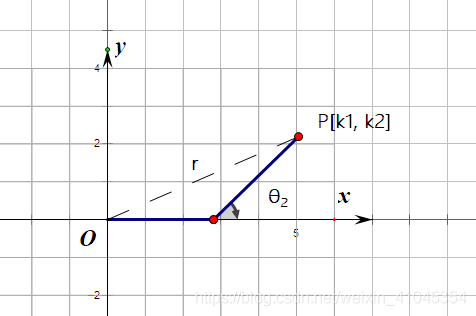
 最终化简成:
最终化简成:  同样使用atan2函数计算得到:γ+α=atan2(y,x) 最终:
同样使用atan2函数计算得到:γ+α=atan2(y,x) 最终:  整理一些写成可计算的python程序如下:
整理一些写成可计算的python程序如下:
c2 = (-L1**2 - L2**2 + x**2 + y**2)/(2*L1*L2)
s2 = np.sqrt(1-c2**2)
# 根据关节配置方式我们取beta为正
theta_2 = np.arctan2(s2, c2)
theta_1 = np.arctan2(y, x) - np.arctan2(L2*s2, L1+L2*c2)
注意
以上求出的θ1是与x轴正半轴的夹角,需要根据机器人的腿部初始角度进行一定变换,例如图中这样腿部初始角度是与地面垂直的,θ1=θ1+90°,θ1是与y轴负半轴的夹角,如最开始的那张图所示