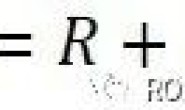传递函数
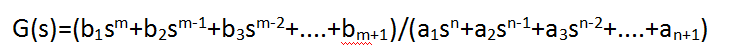
num=[b1 b2 b3 …… bm+1]
den=[a1 a2 a3 …… an+1]
传递函数表示:
sys=tf(num, den)
零极点表示(分子是零点z,分母是极点p):
ss=zpk(sys)
相互转化:
[z,p,k]=tf2zp(num,den)
[num,den]=zp2tf(z,p,k)
部分分式展开:
[r,p,k]=residue(num.den)
系统串、并联、反馈计算
串联:sys=series(sys1,sys2)
并联:sys=parallel(sys1,sys2)
反馈:sys=feedback(sys1,sys2,-1)
单位反馈:ys=cloop(sys1,-1)0
时域分析
阶跃函数、脉冲函数
[y,x]=step(sys,t) or [y,x]=step[sys]
Step/impolse/
加t,选定仿真的时间,不加,系统自动选择。
[y,x]=lsim(sys,u,t)
Gensig 对Lsim产生输入信号
Stepfun 产生单位阶跃输入
频域分析

频率响应曲线的绘制:
[m,p]=bode(num,den,w); or [m,p]=bode(num,den)
[m,p]=nyquist(num,den,w); or [m,p]=nyquist(num,den)
w为频率点构成的向量,该向量最好由logspace()函数生成
幅值裕量和相位裕量
[Gm,Pm,wcg,wcp]=margin(num,den)
其他常用频域分析函数
bode———–频率响应伯德图
nyquist——–频率响应奈奎斯特图
nichols——–频率响应尼柯尔斯图
freqresp——求取频率响应数据
margin——–幅值裕度和相位裕度
pzmap——–零极点图
系统稳定分析
[z,p]=tf2zp(num,den)—–求零极点
pzmap(num,den)———-画出零极点
ii=find(real(p)>0)———–极点有正实部则系统不稳定
>> s1=tf([40],[0.005,0.15,1,0])
>> nyquist(s1)
>> bode(s1)
>> [Gm,Pm,Wcg,Wcp]=margin(s1)
根轨迹
rlocus(num,den) or rlocus(A,B,C,D)
例如:
G(s)=K/s(s+2)(s+5);
num=[1]
den1=[1 2 0]
den2=[1 5]
den=conv(den1,den2)
rlocus(num,den)
v=[-10 10 -10 10]
[k,p]=rlocfind(num,den)
Z变换与反变换
例如:将x(kx)=kT的z变换
syms k T
x=k*T
X=ztrans(x)
例如:求Y(z)=z/(z-1)的z反变换
syms z
Y=z/(z-1)
y=iztrans(Y)
连续函数的离散化
sysD=c2d(sysC,Ts,method)
sysC可以为:
sysC=tf(num,den) or sysC=zpk(z,p,k) or sysC=ss(A,B,C,D)
method可以为:
‘zoj’———–零阶保持器法
‘foh’———-一阶保持器法
‘imp’———冲激响应不变法
‘tustin’——双线性变换法
‘prewarp’–带有预校正的双线性变换法
‘matched’–零极点匹配法
Ts为采样周期取值;