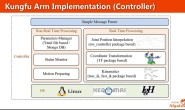
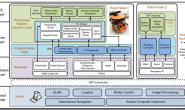
本文转载自微信公众号ROBOTICS 上一篇文章我们讲了机械臂控制的不同对象和方法,以及简单的单关节位置控制。从单关节的控制讲起不仅因为关节控制是机械臂整体控制的基础,也因为了解单关节控制可以帮助我们之后更好地理解看起来会复杂得多的多自由度整机控制。这一篇我们就来讲讲单个关节的阻抗控制。
阻抗是什么?——电路系统与机械系统的类比
位置或者力/扭矩都是大家熟知的物理概念,阻抗/导纳又是什么呢?其实,这是一个从电路里借来的概念。我们知道,在电路中,阻抗是电阻、电感和电容对电流的阻碍作用的统称,它是一个复数:实部是电阻R,虚部则是电抗X。![]() 阻抗为什么是一个复数呢?这是因为它不仅要表示在特定电压输入时电流的大小,还要表示电流相对于电压相位的延迟。欧姆定律告诉我们,电路中的电压与电流的比值就是电阻R
阻抗为什么是一个复数呢?这是因为它不仅要表示在特定电压输入时电流的大小,还要表示电流相对于电压相位的延迟。欧姆定律告诉我们,电路中的电压与电流的比值就是电阻R![]() 把这个式子扩展到阻抗,我们会有
把这个式子扩展到阻抗,我们会有![]()
对下面这样一个电路: 我们有,
我们有,![]() 拉普拉斯变换求出电流到电压的传递函数,则有
拉普拉斯变换求出电流到电压的传递函数,则有 为了求得这个系统的频率响应,设s=jw,我们有
为了求得这个系统的频率响应,设s=jw,我们有![]() 这个时候,这个电路的阻抗已经呼之欲出:
这个时候,这个电路的阻抗已经呼之欲出: 可以看到,电路上的阻抗其实正是从电流到电压的传递函数。 看完电路的阻抗,我们来看看机械上的阻抗。电路里的电压(电动势)就好比推动电子们往前走的一股神秘力量,它对应了物理上的“力”;电路里的电流可以看成是电子们的平均运动速度,它对应了物理上的“速度”;在物理上,对应电阻R,表示力与速度的关系的这个物理量,正是“阻尼”(damping),我们把它记为b。我们知道,阻尼产生的阻力应该与速度成正比:
可以看到,电路上的阻抗其实正是从电流到电压的传递函数。 看完电路的阻抗,我们来看看机械上的阻抗。电路里的电压(电动势)就好比推动电子们往前走的一股神秘力量,它对应了物理上的“力”;电路里的电流可以看成是电子们的平均运动速度,它对应了物理上的“速度”;在物理上,对应电阻R,表示力与速度的关系的这个物理量,正是“阻尼”(damping),我们把它记为b。我们知道,阻尼产生的阻力应该与速度成正比:![]() 现在来看电感L,我们知道,V= L(di/dt), 那么F=什么乘以(dv/dt)呢?你肯定发现了,根据牛顿第二定律,我们有
现在来看电感L,我们知道,V= L(di/dt), 那么F=什么乘以(dv/dt)呢?你肯定发现了,根据牛顿第二定律,我们有![]() 也就是说,质量或者说“惯性系数”m,正对应了电路中的电感L。
也就是说,质量或者说“惯性系数”m,正对应了电路中的电感L。


阻抗控制要做什么?
从上面的类比中我们已经知道,阻抗/导纳表述的是力和运动(位置/速度/加速度)的关系。试想,如果我们只控制运动,那么机械臂的末端在接触到外界物体时必然会对外界施力,并且施力的大小将取决于所采用的运动控制器以及外界物体的特性——这个力是不受我们直接控制的;如果我们只控制末端的力,那么末端的位置必然需要产生相应的改变,这个位置的改变将取决于机械臂本身以及与它产生接触的外界物体的特性, 同样不受我们直接控制。 牛顿定律告诉我们,力是物体运动状态变化(速度变化)的原因,我们不可能不符合物理规律地同时控制力与运动:在方块弹簧的例子中,我们不可能设定一个要求方块对外界施加一个恒定的力,同时要求保持方块在特定点不动的控制目标,这只有在刚好有个能合乎这个要求的障碍物存在的情况下才可能实现。 比起去分别设定“符合物理规律”的力和位置的控制目标,我们不如去设定能够决定位置/速度/加速度如何随着力改变的量、或者对外输出的力如何随着位置/速度/加速度变化的量,也即“阻抗”/“导纳”。比如说,在方块弹簧的例子中,我可以设定这样一个小目标:当我迎面撞上这个方块时,我好像撞到了一块软软的海绵上——即使它连着的弹簧其实很硬。 你可能已经总结出来了,在阻抗控制中,我们的控制目标既不是力、也不是位置,而是这个方块对外界所表现出的动力学特性。
阻抗控制的两种方法
我们知道,“阻抗”是不可直接测量的,因为它表述的是力与运动的关系。阻抗控制的需要的是位置传感器和/或力传感器的反馈。很自然的,控制阻抗可以有两种思路: 1. 根据当前的运动状态,以及目标阻抗,决定输出的力; 2. 根据当前的受力状态,以及目标导纳(阻抗的倒数),决定输出的运动指令。 这样,我们可以非常简化地画出两种方法各自的框图。 第一种:
 这里外环是阻抗环,内环是力矩环,有时候力矩传感器会被省掉,直接用电流做开环力矩控制。 第二种:
这里外环是阻抗环,内环是力矩环,有时候力矩传感器会被省掉,直接用电流做开环力矩控制。 第二种:
 这里外环是阻抗环,内环是位置环(运动控制环),位置环我们通常都会做闭环控制。 这两个框图只展示了阻抗控制两种方法的基本框架,具体的阻抗/导纳控制器设计、它们各自如何实现,我们下面分别来讲。
这里外环是阻抗环,内环是位置环(运动控制环),位置环我们通常都会做闭环控制。 这两个框图只展示了阻抗控制两种方法的基本框架,具体的阻抗/导纳控制器设计、它们各自如何实现,我们下面分别来讲。
基于内环力控制的阻抗控制
我们还是用方块弹簧的例子,控制目标是当你撞上方块时你以为它后面是一块海绵。当你撞上方块,它会测量到一定的位置变化,此时阻抗控制器的目标是输出一个力使得你感受到的弹簧弹性系数(k_d)很低、阻尼系数(b_d)类似海绵、惯性(m_d)也不太大。 如果阻抗控制器不存在的话,那么系统的响应将会遵循下面这个动力学方程,其中f_ext表示外界对系统施加的力(也就是你撞上去的力),并且假设弹簧的原点是0:
![]() 而阻抗控制的目标则是要把系统响应变成下面这样的动力学方程,其中{md, bd, kd}即是我们希望系统对外表现出的惯性、阻尼、刚性特征(仍然假设我们的位置原点是0):
而阻抗控制的目标则是要把系统响应变成下面这样的动力学方程,其中{md, bd, kd}即是我们希望系统对外表现出的惯性、阻尼、刚性特征(仍然假设我们的位置原点是0):
![]() 从上面两个式子,我们可以得到阻抗控制器需要输出的力f_d为
从上面两个式子,我们可以得到阻抗控制器需要输出的力f_d为
![]() 你肯定发现了,在这个方法里,我们需要知道系统本身的动力学模型{k, b, m},才能准确计算出所需的力,有时候我们也称之为基于模型的阻抗控制(model-based impedance control)。另外,用这个方法也很难让系统呈现比较大的刚性(设一个很大的k_d)——当k_d很大时,微小的测量位置变化即会引起很大的力指令变化,系统会非常容易不稳定。 通常情况下,我们可以不对系统呈现的“惯量”进行控制。另外,上述的分析为了简化等式假设参考的位置/速度都为0。如果我们忽略惯量/加速度项,并把理想的方块位置原点记为x_d,阻抗控制可以写作如下形式:
你肯定发现了,在这个方法里,我们需要知道系统本身的动力学模型{k, b, m},才能准确计算出所需的力,有时候我们也称之为基于模型的阻抗控制(model-based impedance control)。另外,用这个方法也很难让系统呈现比较大的刚性(设一个很大的k_d)——当k_d很大时,微小的测量位置变化即会引起很大的力指令变化,系统会非常容易不稳定。 通常情况下,我们可以不对系统呈现的“惯量”进行控制。另外,上述的分析为了简化等式假设参考的位置/速度都为0。如果我们忽略惯量/加速度项,并把理想的方块位置原点记为x_d,阻抗控制可以写作如下形式:
![]() 你会发现,这个式子与关节位置控制所用的PD控制的式子是非常相似的!在关节位置控制中,我们通常会选取适当的P和D的控制系数,使得系统在稳定的前提下刚性尽可能的高,以实现快速精确的轨迹跟踪。而在阻抗控制中,为了实现接触的柔性(比较低的k_d,也即比较低的P gain),则需要以牺牲轨迹跟踪的精度和速度为前提。
你会发现,这个式子与关节位置控制所用的PD控制的式子是非常相似的!在关节位置控制中,我们通常会选取适当的P和D的控制系数,使得系统在稳定的前提下刚性尽可能的高,以实现快速精确的轨迹跟踪。而在阻抗控制中,为了实现接触的柔性(比较低的k_d,也即比较低的P gain),则需要以牺牲轨迹跟踪的精度和速度为前提。
基于内环运动控制的阻抗控制
现在同样的控制目标用第二种方法来实现:当你撞上方块,它会测量到方块的受力,并计算出理想的运动轨迹使你感觉好像撞在海绵上。这时候,我们依然希望系统的状态方程如下(仍然假设位置原点为0):
![]() 通常,我们通过位置传感器获得方块当前的位置以及运动速度,并求出理想的加速度以实现设定的阻抗目标。我们有
通常,我们通过位置传感器获得方块当前的位置以及运动速度,并求出理想的加速度以实现设定的阻抗目标。我们有
 求出理想的加速度后,我们就可以根据当前的位置和速度求出理想的位置/速度指令,使系统呈现出我们理想的阻抗。
求出理想的加速度后,我们就可以根据当前的位置和速度求出理想的位置/速度指令,使系统呈现出我们理想的阻抗。
 这个方法可以很好地利用现在已非常成熟的位置控制算法来实现精度和响应都比较好的导纳控制。另外,它也不需要依赖系统本身的动力学参数。但是可以看到,处在分母的m_d项使得我们很难让系统呈现比较小的质量/惯性——很小的扰动即可能造成很大的运动指令变化,系统也容易不稳定。 类似在第一种方法中在阻抗控制的同时对位置进行跟踪,我们也有可能在导纳控制的同时对接触力进行跟踪。不难想象,在静态情况下,如果接触力(f_ext)与我们理想的力之间存在误差,我们可以通过调节位置原点,或者理想刚度k_d来改变这个力。具体的力跟踪算法我们在下一篇文章中讨论。
这个方法可以很好地利用现在已非常成熟的位置控制算法来实现精度和响应都比较好的导纳控制。另外,它也不需要依赖系统本身的动力学参数。但是可以看到,处在分母的m_d项使得我们很难让系统呈现比较小的质量/惯性——很小的扰动即可能造成很大的运动指令变化,系统也容易不稳定。 类似在第一种方法中在阻抗控制的同时对位置进行跟踪,我们也有可能在导纳控制的同时对接触力进行跟踪。不难想象,在静态情况下,如果接触力(f_ext)与我们理想的力之间存在误差,我们可以通过调节位置原点,或者理想刚度k_d来改变这个力。具体的力跟踪算法我们在下一篇文章中讨论。
关节阻抗控制两种方法的对比总结
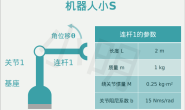
上文中用方块弹簧的例子,实际上,我们通常把关节建模为一个由质量块、弹簧、阻尼器组成的二阶系统(这里我们先不考虑摩擦力),关节的阻抗控制与上文所讲的例子是非常一致的。下面这个表格用旋转关节所用的符号再总结一下阻抗控制的两种方法。为了简化,我们假设关节的参考位置/速度都为0。
 这篇文章希望用尽可能简单的方式为大家介绍阻抗/导纳的概念以及阻抗/导纳控制的两种基本思路。理解了一个维度的阻抗控制将有助于我们后续理解整个机械臂的阻抗控制——你会发现,它们在基本形式上是非常相似的。
这篇文章希望用尽可能简单的方式为大家介绍阻抗/导纳的概念以及阻抗/导纳控制的两种基本思路。理解了一个维度的阻抗控制将有助于我们后续理解整个机械臂的阻抗控制——你会发现,它们在基本形式上是非常相似的。