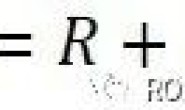干货 | 机械臂控制第0篇：什么是控制？

​本文转载自微信公众号ROBOTICS 我们学习了那么多机械臂的运动学和动力学，归根结底还是为了能控制机械臂做我们希望它做的事情。从这一篇开始，我们就来聊聊机械臂的控制。（对的，CC终于开始写机械臂控制了！） 控制——大道至简 控制这门学问，大概是工程学科里最有艺术感的——为什么这么说呢？因为它的根本思想简单至极，却用途广泛、影响深远，正可谓“大道至简”。 反馈控制的基本思想，可以用下面这个框图表示： 用通俗的语言说（其实熟悉了以后你会发现文字远不如框图表述得清楚），这个框图描述了反馈控制的四个步骤： 第一，r作为”reference input”（参考输入），告诉控制器你对需要控制的变量的期望值； 第二，uc作为控制器输出的控制信号，经过系统的执行器，输出信号u去操控被控系统； 第三，系统自己的动力学特性决定了在u的作用下，输出的y会是什么样子的； 第四，这个输出y通过传感器反馈回控制器，与期望做比较，然后控制器再根据这个比较的结果调节自己的输出（回到第一步）。 通过不断的四步循环，通过合理地设计控制器，系统的输出最终会逼近你想要的参考输入值。 一个框图加上三言两语可能太抽象，其实人类自己身上就有许多这样的控制系统。以体温调节举例，百科上说：“体温调节是指温度感受器接受体内、外环境温度的刺激，通过体温调节中枢的活动，相应地引起内分泌腺、骨骼肌、皮肤血管和汗腺等组织器官活动的改变，从而调整机体的产热和散热过程，使体温保持在相对恒定的水平。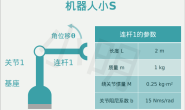”把这个过程套进控制框图里就一目了然了： 你还能发现人体内的其他控制系统吗？   开环控制（Open Loop Control）   要想了解为什么控制框图一定要是一个环，我们需要先来看看没有传感器的“控制”是什么样的，为此我要拿出最爱用的方块弹簧作为例子。 现在假设有一个弹簧，一头连在墙上，另一头连着一个方块，现在要你把方块从A点拉到B点并停下，你一定觉得这个任务太简单了吧？但如果用一个“拉力发生器”连在方块上，由你来决定每个时刻它施加的拉力f 的大小和方向，这个问题可就没那么简单了。 我们就从最简单粗暴的方法开始——既然是要在B点停下，我们就施加一个与弹簧在B点的拉力大小相等、方向相反的恒力好了，像这样（k是弹簧的弹性系数）: 很快我们就会发现，用这个力把方块从A点拉到B点，那么方块到达B点时速度一定不为零。事实上，它会越过B点，一直运动到距B点的距离和A点距B点的距离相等的地方（我们称它为A’点），然后在A点和A‘点之间来回震荡。 如果依靠一点物理知识写出这个“弹簧方块系统”的动力学模型表达式（为了方便我们把A点设为零点、并且假设没有摩擦力），我们会发现好像只要决定了x(t)（方块的位置随时间的函数），那么f(t)（拉力随时间的函数）就可以轻易地求出来： 好像问题这就解决了？并没有！——现实世界是不完美的：我们所知的方块质量m可能离真实值差了一点；我们所知道的弹簧的k也不是那么准确；我们的拉力发生器更加不靠谱，你让它出的力气它总是要打点折——在这种种的不完美下，你发出了f(t)的命令，方块最终可能离B点有十万八千里。 上面用的两种方法，一种是瞎猜、一种是列出了系统的动力学方程——无论哪一种，我们所施加的力与方块在实际运动过程中所处的位置/状态没有半点关系，没有传感器把这些信息反馈回控制器——我们把这种方法称为开环控制。   闭环控制（Close Loop Control）     继续看方块弹簧的例子：我们为什么不时刻看一看这个方块到哪儿了、跑多快、离B点多远，然后再决定我要施加多少力呢？ 闭环控制最简单的方法，就是时刻检测方块的实际位置（以及速度和加速度）——它比预计的快了，那就把力调小一点；慢了呢，就调大一点。方块的实际位置与预计位置的差反馈给了“控制器”，这种方法就叫负反馈控制。 比如说，我们让这个力与方块距B点的距离成正比: 然后我们就能把这个控制器和系统的动力学方程（的频域表达式）都套入到一开始给出的控制框图里，方便我们对系统进行分析：   大家可以看到，在框图中被控系统的表达式采用了系统在时域上的动力学方程经过拉普拉斯变换得到的频域表达式。拉普拉斯变换（Laplace Transform）可以说是传统控制理论里的强大武器。为什么要转到频域去看呢？我们可以先看看这个系统在没有外力作用时的时域方程： 可以看到，这是一个二阶线性微分方程。给定初始值，要怎么解这个方程呢？——不好意思地说，我都有些不记得了，只依稀记得它的解里会有e的多少次方，利用欧拉公式，可以把它变成正弦余弦的形式…… 那么这个时域方程用拉普拉斯变换之后呢？很神奇的，微分的部分不见了，它变成了一个代数方程： 然后我们可以解出来 在时域上求得的解是x(t)，这里的t是时间，这个解告诉我们x随时间t的变化；经过拉普拉斯变化，我们在频域上求得的解是X(s)，这里的s是复平面上的一个点——当s = jw（w是角频率，即频率f/2π）时，它表示一个频率——这样我们可以得到X与频率w的关系。 我们发现，当s使分母为0时，X会变无限大，这个时候可以求得 它告诉我们这个系统的一个重要特性——它的共振频率（natural frequency）是w = 根号k/m。基本上一个很小的扰动就足够让系统以这个频率来回震荡；而这个使分母为0的点，我们称之为”极点“。 转到频域有许多显而易见的好处。首先是对复杂微分系统，在频域上的运算都是代数运算，非常方便；其次从频率这个角度去认识一个系统，能让我们对系统的特性有更宏观也更直观的认知。在拉普拉斯变换和复平面的概念之上，传统控制理论发展了很多用于分析系统特性、调节控制器参数的方法，比如方框图代数（Block Diagram Algebra）、零极点分析（Pole-Zero Analysis)、伯德图（Bode Plot）、奈奎斯特图（Nyquist Plot）等等。 我们知道在不加任何控制器的情况下，这个弹簧方块系统只要初始状态不为0，就会以特定的频率来回振荡。如果在这个系统中加入P Control会有什么效果呢？首先我们可以利用“方框图代数”来求得这个系统的传递函数： 则： 做一下零极点分析（解分母=0的方程可以求出极点），我们发现这个闭环系统依然类似原本的弹簧方块系统；方块依然是不停地来回振荡，只不过频率从根号k/m变成了根号（k+kp)/m！ 从另一个角度说，P Control的效果其实就相当于改变系统的弹性系数（Stiffness）。 这个例子中由于我们假设没有摩擦力，要让系统的输出不要总是来回振荡，而是可以最终收敛到一个恒定的值，我们需要给系统加一点阻尼（damping）。加阻尼的方法则是通过让控制器的输出和方块位置对时间的微分（也就是方块的速度）误差成正比：D Control的作用相当于改变系统的阻尼系数（damping）。 合适的P和D系数可以保证方块最终会停在某处，但不能保证它一定会停在我们要的B点，这时方块实际位置与B点位置的差被称为稳态误差（Steady state error）。要消除稳态误差就需要I Control 来发挥它的作用：I Control使控制器的输出与方块位置的误差对时间的积分成正比——如果误差一直没有消除，那么控制器的输出就会越来越大。 即便上面的拉普拉斯变换、时域、频域、零极点等等你都不了解，我想你也已经抓住了最经典的控制方法——PID控制的精髓：根据每一时刻现实与目标的距离、奔向目标的速度与理想的速度（是的，奔太快也不好，容易跑过头）、一段时间内与目标之间的误差之和来随时调整控制器的输出。PID（有时只有PD，有时是PI）控制在工业和生活的各种地方都在默默地工作，它所蕴涵的思想既简单又深刻。   总结   这篇文章是为了后续写机械臂的控制而作，并不是专门讲控制理论的一篇；所以我们不讲各种分析、计算的方法，只求讲清楚概念。 最后我要在再说一遍——我觉得控制是最具艺术感的一门工程学科，它的存在，是为了我们能用超越时间的视角去认识各个不断演化的系统、是为了我们总能朝着目标不断调整逼近而不渐行渐远、是为了应对我们认知的缺陷与这个世界本身的不完美——学好控制论，走遍天下都不怕。