三维情况实际上是之前讨论的二维情况的延伸。我们在二维坐标系上增加一个额外的坐标轴,通常用 z 表示,它同时与 x 轴和 y 轴正交。 z 轴的方向服从右手规则,并构成右手坐标系。与各坐标轴平行的单位向量记作 x、 y 和 z

坐标系中的一个点 P 可用其 x, y 和 z 的坐标值 (x, y, z) 或者一个约束向量表示:

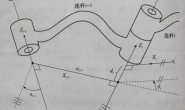
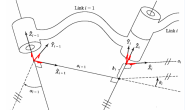
下图展示了一个相对于参考坐标系 {A} 的坐标系 {B} 。可以清楚地看到, {B} 的原点通过向量) t=(x,y,z) 进行平移,然后再通过某种复杂方式进行了旋转。正如二维情况一样,我们如何表示坐标系之间的方向是非常重要的。

我们的做法还是从相对于每个坐标系的任意一点 P 出发,然后再确定 AP 和 BP 之间的关系。我们仍然从两方面考虑:旋转和平移。
三维空间姿态描述
任何两个独立的正交坐标系都可以通过一系列(不超过3次)相对于坐标轴的旋转联系起来,但其中连续的两次旋转不能绕同一轴线。
——欧拉旋转定理
之前的图中显示了两个右手坐标系,其方向差异很大,我们如何相对于一个坐标系去表示另一个坐标系呢?可以想象一下,将坐标系 {A} 拿在我们手里旋转,直到与坐标系 {B} 方向一致。欧拉旋转定理指出,任何旋转都可以看作是由一系列相对不同坐标轴的旋转组合而成的。
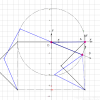
首先考虑绕单个坐标轴的旋转。下图显示了一个右手坐标系,以及它绕不同坐标轴旋转不同角度的情形。

但绕坐标轴连续旋转就没那么简单了,其中存在一些微妙的变化。如下图所示,它演示了一个坐标系按不同的顺序旋转的情形。可以看到,虽然旋转角度相同,但最终得到的坐标系方向完全不同,它取决于旋转的顺序。这是三维世界里一个深奥且让人迷惑的特征,而且它曾困扰了数学家们很长一段时间。我们之前一直在讨论的位姿代数的意义就在于运算符 ⊕ 是不可交换的,它体现了上述旋转顺序的重要性。下图中,在上面一排中坐标系先绕 x 轴旋转 π/2,然后绕 y 轴旋转 π/2。在下面一排旋转顺序正好颠倒了。两种旋转的结果明显不同。

数学家已经提炼出许多表示旋转的方法,我们之后会讨论其中几种:正交旋转矩阵,欧拉和卡尔丹角,旋转轴与角度,以及单位四元数。它们都可以表示为向量或矩阵,即MATLAB的自然数据类型,或者表示为机器人工具箱自定义的类。机器人工具箱中提供了许多函数可以将这些表示法相互转换,我们后面也会有介绍。