机器人学——1.3-正交旋转矩阵

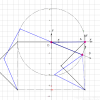
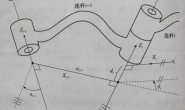
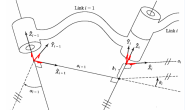
正如在二维情况下一样，我们可以用相对于参考坐标系的坐标轴单位向量表示它们所在坐标系的方向。每一个单位向量有 3 个元素，它们组成了 3×3 阶正交矩阵 ^AR_B ：

上式将一个相对于坐标系 {B} 的向量旋转为相对于坐标系 {A} 的向量。矩阵 R 属于特殊三维正交群，或
 。它具有前文提到的标准正交矩阵的特性，如 R^T= R⁻¹以及 det(R) = 1。
分别绕 x， y， z 轴旋转 θ 角后的标准正交旋转矩阵可表示为

机器人工具箱中也提供了一些函数来计算这些基本的旋转矩阵，例如 R_x(θ) 是

>> R = rotx(pi/2)
R =
    1.0000         0         0
         0    0.0000   -1.0000
         0    1.0000    0.0000

函数roty和rotz则分别用于计算 R_y(θ)和 R_z(θ) 。
要绘制出相应的坐标系，可以用

>> trplot(R)

如图所示

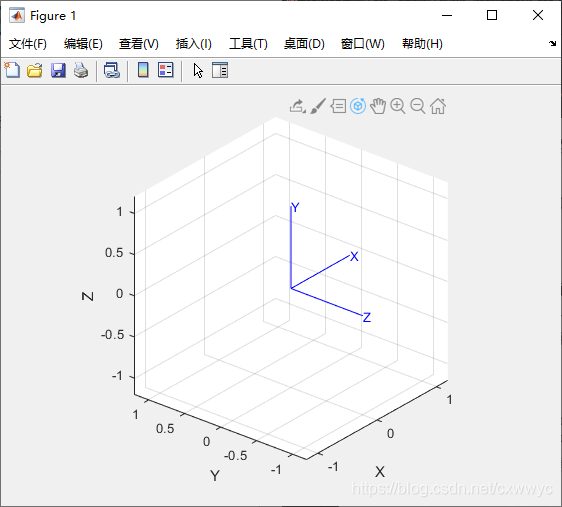
如果要想使一个旋转更加生动有力，可以使用工具箱函数tranimate制作一个旋转动画：

>> tranimate(R)

它将展示世界坐标系旋转到指定坐标系的过程。

在正交旋转矩阵中，从左至右的列向量可以告诉我们旋转后新坐标系各个轴相对于当前坐标系的方向。例如，如果

R =
   1.0000         0         0
        0    0.0000   -1.0000
        0    1.0000    0.0000

则新坐标系的 x x x 轴仍在以前 x x x 轴方向 (1，0，0) ，但其 y y y 轴却在以前的 z z z 轴方向 (0，0，1) ，而新的 z 轴在以前 y y y 轴的反方向  (0，-1，0) 。这里，之所以 x 轴没变，是因为这个旋转是围绕 x 轴发生的。行向量则相反，它们表示了原来坐标系的各个轴在新坐标系中的方向。

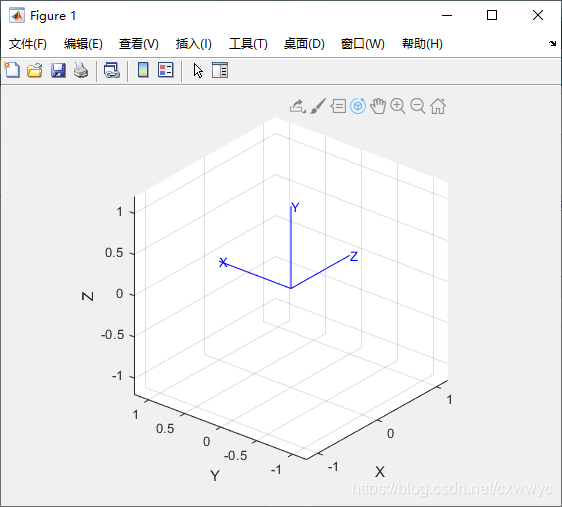
为了说明旋转的复合，我们继续旋转上一张图所示的坐标系，这一次绕它的y轴旋转：

>> R = rotx(pi/2) * roty(pi/2)
R =
    0.0000         0    1.0000
    1.0000    0.0000   -0.0000
   -0.0000    1.0000    0.0000
>> trplot(R)

绘制出如图所示的坐标系。在这个坐标系中， x 轴现在指向世界坐标系 y 轴的方向。

如果颠倒以上旋转的顺序，可以看出旋转的不可交换性：

>> R = roty(pi/2) * rotx(pi/2)
R =
    0.0000    1.0000    0.0000
         0    0.0000   -1.0000
   -1.0000    0.0000    0.0000
>> trplot(R)

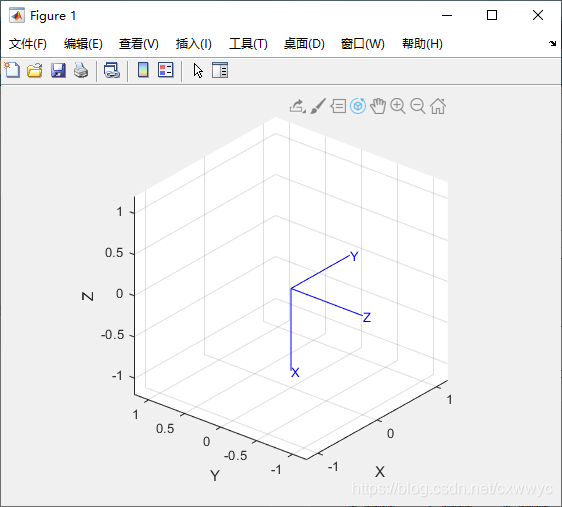
得到的结果是完全不同的。

回忆一下欧拉旋转定理，它指出任何旋转都可以用不超过 3 次绕坐标轴的旋转表示。这意味着，一般情况下两个坐标系之间的任意旋转均可分解为一组绕三个旋转轴转动的角度——这个问题之后讨论。
正交矩阵有 9 个元素，但它们不是独立的。每一列都是单位长度，这提供了 3 个约束。列与列之间相互正交，又提供了另外 3 个约束。 9 个元素加上 6 个约束，实际上只有 3 个独立的值。