小伙伴们似乎对RRT有种莫名的期待，从大概四个月前，我第一次更新运动规划入门系列的时候就有小伙伴催着要看RRT了，那么今天就满足你们。书接上回，我们上次讲完了PRM，我们知道PRM是一个概率完备，但是非最优的路径规划算法。所谓概率完备，意思就是说假如在规划的起点和终点之间是存在有效的路径的，也就是路径规划是有解的话，那么只要规划的时间足够长、采样点足够多的话，必然可以找到有效的路径。非最优就很好理解了，说白了就是PRM能找到解但是不保证是最好的解。这次要讲的RRT和PRM一样也是一个概率完备的非最优的路径规划算法。

1. 原理图解：

Rapidly Exploring Random Trees 快速探索随机树，RRT和PRM的相同之处是，它们都是基于随机采样的规划算法，不同的是PRM生成的是一个“图”（Graph），而RRT生成的是“树”，RRT的一大显著特征就是它具备探索空间的能力，即从一点（根）出发向外探索拓展的特征。简单的RRT有单树和双树两种类型，单树RRT将规划起点作为随机树的根节点，通过随机采样、碰撞检测的方式为随机树增加叶子节点，最终生成一颗随机树。而双RRT则拥有两颗随机树，分别以起点和终点为根节点，以同样的方式进行向外的探索，直到两颗随机树相遇，以达到提高规划效率的目的。

1.1 RRT

首先我们从单树RRT开始讲起，在上一篇讲PRM的时候，我已经详细介绍过随机采样、步长限制、碰撞检测等等概念以及实现方式。这些PRM必要的步骤，在RRT中同样不可或缺。在这我就不再赘述，如果对以上概念和实现方式不太熟悉的话，可以先去看上一篇博文。 RRT的运行原理对于初次接触的小伙伴来说可能不是很好理解，所以我们就不要一上来就讲算法流程。不如我先带你来一次“大脑仿真”。首先给你一张已知的地图，就还是用上次PRM那张示意图吧（偷懒）。起初我们只有两个节点，一个绿色的起点和一个黄色的终点。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现对于单树RRT，我们做的第一件事就是将起点设置为随机树的根。那么其实此时我们就已经拥有了一颗随机树了，只不过这棵树只有一个根节点而已。
这棵树光秃秃的，只有根节点的话不但难看，而且还没用。那么我们这时候就需要从这个根节点出发，向外拓展出新的叶子。拓展的方式很简单，就是随机采样+步长限制+碰撞检测。 RRT在每轮迭代中会生成一个随机采样点NewNode，如果NewNode位于自由区域，那么我们就可以遍历随机树中已有的全部节点，找出距离NewNode最近的节点ClosestNode。利用距离函数dist(NewNode, ClosestNode)得到二者之间的距离，如果满足步长限制的话，我们将接着对这两个节点进行碰撞检测，如果不满足步长限制的话，我们需要沿着NewNode和ClosestNode的连线方向，找出一个符合步长限制的中间点，用来替代NewNode。最后如果NewNode和ClosestNode通过了碰撞检测，就意味着二者之间存在边（edge），我们便可以将NewNode添加进随机树中。首先以第一轮迭代为例，因为刚开始我们的随机树中只有根节点，所以无论NewNode位于何处，遍历出的最近节点ClosestNode必然是根节点。假设我们遇到下图这种情况，虽然采样点NewNode位于步长限制之内，但是却很不巧没有落在自由区域，即采样点落在障碍物的位置时，这个采样点会被算法舍弃。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现假设我们的步长限制为R，也就是说对于每个ClosestNode节点来说，只有当NewNode落在其半径为R的圆的范围内时，这个随机采样点NewNode才有可能被直接采纳。如下图所示，该红色随机采样点虽然位于自由区域，但是明显在根节点的步长限制之外。不过这个节点并不会被简单粗暴地舍弃。而是会沿着ClosestNode和NewNode的连线，找出符合步长限制的中间点，将这个中间点作为新的采样点。如下图所示，蓝点就可以替代红点作为新的采样点。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现那么假设我们已经通过第一轮迭代拓展出第一个叶子节点A，毫无疑问地A的父节点就是根节点，假设我们第二轮迭代的随机采样点NewNode为图中的点B，B落在A的步长限制范围内，但是A，B之间由于障碍物的阻挡，无法通过碰撞检测，于是B就会被算法舍弃。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现假设我们的随机采样点是下图中的B’，明显B’位于自由区域，满足步长条件，并且可以通过与点A的碰撞检测，那么我们就在B’和A之间添加一条边，并且将A设置为B’的父节点。学过数据结构的小伙伴一定知道，在树结构中每个节点最多只有一个父节点，父节点可以拥有多个子节点。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现在经历了N轮迭代后，我们已经获得了一颗如下图所示的随机树，这时我们发现此时的随机采样点竟然幸运地落在了终点的步长限制范围内，并且二者之间不存在障碍物。这时我们便可以认为，该采样点和终点之间存在一条边，于是将该节点设为终点的父节点，并把终点添加进随机树。此时算法就可以结束迭代了，即规划算法收敛。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现当规划算法收敛以后，只需要从终点开始，沿着其父节点进行回溯，就可以找到起点-终点之间的有效路径。
那么总结一下，RRT生成的每轮迭代中都包含以下这些流程：

生成一个随机采样点NewNode，并判断采样点是否位于自由区域
遍历随机树，找出距离NewNode最近的节点ClosestNode
判断NewNode是否在ClosestNode的步长限制范围内，否则寻找中间点替代NewNode
判断NewNode和ClosestNode之间是否存在障碍物，即碰撞检测。
如果NewNode满足以上所有约束条件，则将NewNode添加进随机树，设置ClosestNode为NewNode的父节点。
判断NewNode是否在终点的步长限制范围内，并对其二者做碰撞检测。如果满足条件则将该NewNode设为终点的父节点，并将终点加入随机树，即可结束迭代。否则继续迭代。

从以上流程中，我们可以看出，由于算法在未达到收敛条件之前是在不断进行迭代的，所以只要在规划的起点和终点之间是存在有效的路径，那么只要迭代的次数够多，那么采样点就够多，随机树就长得越茂密，能探索到的区域就足够广，就必然可以找到有效的路径。所以RRT是概率完备的。但是由于采样点每次都是随机的，所以算法并不能保证找到的路径是最优的路径。因此RRT是非最优的。

1.2 双树RRT

双树RRT是在原本RRT的基础上多加了一颗随机探索树，各自从起点和终点向外探索拓展，直到两棵树相遇时规划算法收敛。这种改进过的探索策略可以大大提高RRT的运行效率。双树RRT中存在两颗随机树，我们将其命名为A和B，A以起点为根节点，B以终点为根节点。两颗随机的拓展方式和单树RRT的别无二致，同样都需要经历随机采样+步长限制+碰撞检测这三个步骤，但是不同的地方在于双树RRT的随机树是交替生长的，比方说第一轮迭代中A树向外生长，第二轮便切换为B树生长，如此循环。在每轮迭代中，随机树除了向外拓展之外，还会多出一个步骤，就是遍历另一颗随机树中的所有节点，找出离NewNode最近的节点，用于判断两颗随机树是否相遇。假设算法经历了N次迭代以后，已经拓展出如下图所示的两颗随机树。并且在下一轮迭代中，轮到A树进行拓展，A树在图中用绿色线条表示，B树用黄色线条表示。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现当进入本轮迭代后，算法成功拓展出A树的新节点NewNode_A，此时算法会遍历B树中的所有节点，找出B树中离NewNode_A最近的节点ClosestNode_B。并判断二者是否满足步长限制以及是否可以通过步长检测。如下图所示，这种情况明显无法通过碰撞检测。那么A树和B树在这一轮迭代中无法相遇，需要接着下一轮迭代。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现进入下一轮迭代，这次便切换为B树进行拓展，假设算法拓展出的NewNode_B以及遍历A树后得到的ClosestNode_A如下图所示，经过判断发现二者满足步长限制并且通过了碰撞检测，那么这时A树和B树就成功得相遇了，规划算法收敛。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现当算法收敛以后，只需在两棵树的相遇处分别沿着父节点回溯便可以找出从起点到终点的有效路径。

2. RRT的Matlab实现

RRT中不可或缺的距离函数和碰撞检测函数我直接沿用上次PRM的代码，完全不需要改动。如果又小伙伴不清楚这一部分是如何实现的，可以回去看上一篇博文。在这里我就重点讲一下Node类、中间点选取函数、单树RRT和双树RRT的实现。

2.1 Node类

为了较为方便地实现树的数据结构，我还是根上次的PRM一样，采用Node类来表示节点，并通过创建一个Node的结构体数组node_list来表示树。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现 Node类的定义如下，类的成员包括：

type：节点的类型
coordinate：当前节点的实际坐标
index：当前节点在node_list中的索引
parent_coordinate：父节点的实际坐标
parent_index：父节点在node_list中的索引
cost：与父节点的边的代价值

Node的方法很简单，就一个构建函数，一个SetIndex用于设置节点的索引，一个SetParent用于设置节点的父节点。很好理解。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现

2.2 中间点选取函数

中间点选取函数非常好理解，无非就是高中数学的知识而已，简单地求出矢量的方向角，用最大步长乘以方向角的三角函数，就能直接求出横纵坐标的差值。从而就能得到一个满足步长限制的中间点。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现

2.3 单树RRT核心代码

老样子，需要完整matlab源码的小伙伴可以在评论区找我要，我发邮箱。

while true
    if(iteration_times >= sampling_points || plan_succeeded == 1) % if exceed the sample times or plan succeeded
        break;
    end

    rand_node = [MapSize(1)*rand(1,1), MapSize(2)*rand(1,1)];
    add2list_flag = 0;
    if(map(ceil(rand_node(2)), ceil(rand_node(1))) ~= 2) % if the random node on the free space
        list_size = size(node_list);
        min_dis = inf;
        closest_node_index = 0;
        for i = 1:list_size(1)  % traverse the whole node_list to find closest nodes
            dis = distance(rand_node, node_list(i).coordinate); 
            if(dis < min_dis)
                closest_node_index = i;
                min_dis = dis;
            end
        end

        if(min_dis > step_length_limit) % if the minimum distance is longer than step length limit
            New_Node = Find_Inter_Node(node_list(closest_node_index).coordinate, rand_node, step_length_limit); % we should find a intermediate node.
        else
            New_Node = Node(rand_node, 'N');
        end

        if(ObstacleCheck(New_Node.coordinate, node_list(closest_node_index).coordinate, map, 0.01) == 0)    % if the edge between nodes don't collision with obstacle
            add2list_flag = 1;
            % set parent node
            New_Node = New_Node.SetParent(node_list(closest_node_index).coordinate, distance(New_Node.coordinate, node_list(closest_node_index).coordinate), closest_node_index);
        end

        if(add2list_flag == 1)
            iteration_times = iteration_times + 1;
            list_size = size(node_list);
            New_Node = New_Node.SetIndex(list_size(1)+1);
            node_list = [node_list; New_Node];

            dis = distance(destination, New_Node.coordinate); 
            if(dis <= step_length_limit)    % if the node is close enough to the goal 
                if(ObstacleCheck(New_Node.coordinate, destination, map, 0.01) == 0)
                    plan_succeeded = 1;
                    goal_node = goal_node.SetIndex(size(node_list, 1)+1);
                    goal_node = goal_node.SetParent(node_list(closest_node_index).coordinate, distance(New_Node.coordinate, node_list(closest_node_index).coordinate), closest_node_index);
                    node_list = [node_list; goal_node];
                end
            end
        end
    end
end

2.4 双树RRT核心代码

while true
    if(iteration_times >= sampling_points || plan_succeeded == 1)   % if exceed the sample times or plan succeeded
        break;
    end
    rand_node = [MapSize(1)*rand(1,1), MapSize(2)*rand(1,1)];
    add2list_flag = 0;
    if(map(ceil(rand_node(2)), ceil(rand_node(1))) ~= 2) % if the random node on the free space
        list_size = size(node_list);
        min_dis = inf;
        closest_node_index = 0;
        for i = 1:list_size(1)  % traverse the whole node_list to find closest node
            dis = distance(rand_node, node_list(i).coordinate); 
            if(dis < min_dis)
                closest_node_index = i;
                min_dis = dis;
            end
        end

        if(min_dis > step_length_limit) % if the minimum distance is longer than step length limit
            New_Node = Find_Inter_Node(node_list(closest_node_index).coordinate, rand_node, step_length_limit); % we should find a intermediate node.
        else
            New_Node = Node(rand_node, 'N');
        end

        if(ObstacleCheck(New_Node.coordinate, node_list(closest_node_index).coordinate, map, 0.01) == 0)    % if the edge between nodes don't collision with obstacle
            add2list_flag = 1;
            New_Node = New_Node.SetParent(node_list(closest_node_index).coordinate, distance(New_Node.coordinate, node_list(closest_node_index).coordinate), closest_node_index);
        end

        if(add2list_flag == 1)
            iteration_times = iteration_times + 1;
            list_size = size(node_list);
            New_Node = New_Node.SetIndex(list_size(1)+1);
            if(node_list_flag == 1) % traverse the B tree to find closest node_B
                node_list1 = [node_list; New_Node];
                min_dis = inf;
                for k = 1:size(node_list2,1)
                    dis = distance(node_list1(end).coordinate, node_list2(k).coordinate); 
                    if(dis < min_dis)
                        closest_node_index = k;
                        min_dis = dis;
                    end
                end
                if(min_dis < step_length_limit)
                    if(ObstacleCheck(node_list1(end).coordinate, node_list2(closest_node_index).coordinate, map, 0.01) == 0)
                        plan_succeeded = 1;
                        intersection_point1_index = node_list1(end).index;
                        intersection_point2_index = closest_node_index;
                    end
                end
            elseif(node_list_flag == 2)  % traverse the A tree to find closest node_A
                node_list2 = [node_list; New_Node];
                min_dis = inf;
                for k = 1:size(node_list1,1)
                    dis = distance(node_list2(end).coordinate, node_list1(k).coordinate); 
                    if(dis < min_dis)
                        closest_node_index = k;
                        min_dis = dis;
                    end
                end
                if(min_dis < step_length_limit)
                    if(ObstacleCheck(node_list2(end).coordinate, node_list1(closest_node_index).coordinate, map, 0.01) == 0)
                        plan_succeeded = 1;
                        intersection_point1_index = closest_node_index;
                        intersection_point2_index = node_list2(end).index;
                    end
                end
            end
        end
    end
end

2.5 运行效果

题外话：我发现以前给代码的时候，没有特意讲过代码的使用方式，也许有些不熟悉matlab的小伙伴会对代码的使用产生疑惑，那我就在这里给拿到代码的小伙伴们稍微说一下。 首先是切换地图： 我一般会在代码文件夹中准备两到三张栅格地图，方便小伙伴们做实验。解压文件夹后就能看到以下这三个mat文件。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现在run.m的开头，使用load函数将地图加载进来后，matlab的workspace里就会多出一个叫做map变量，注意：这三张地图load进来以后都是赋给map变量，所以每次只能load进来一份地图，后来的load会覆盖掉前面的load。切换地图也十分简单，只要注释掉在下面这三行代码中的两行，留下你要的那张地图就可以了。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现 还有就是配置参数和切换规划算法： 代码中的需要配置修改的参数不多，基本就是下面这几个，一个起点坐标，一个终点坐标。 show_tree_only用于设置演示效果，设置为true的话就会隐藏掉所有红色的节点，只显示随机树的枝干。 show_animation用于开启和关闭动画演示，其实大部分时间我会关掉动画演示，只有在录制gif的时候才开启一下，毕竟太多的动画会让代码运行时间太长，特别是当随机树很庞大的时候。 sampling_points用于设置随机树的采样点数量，但是在这里我直接将其设置为inf，也就是无穷大，只有不限制采样点的数目，RRT才会一直迭代直到收敛。 step_length_limit这个就很明显了，步长限制就是通过这个变量来设置的。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现
那么言归正传，让我们掏出下面这几张祖传的栅格地图，对规划算法进行一一地测试。首先是20*20的栅格地图：单树RRT在步长限制为2的条件下，运行效果如下图所示：
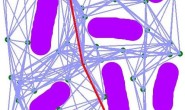
双树RRT在步长限制为2的条件下，运行效果如下图所示：最终绿色的路径是属于A树的，黄色的路径属于B树，而紫色的一小段路径就是两颗随机树相遇的位置。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现当我们将步长限制扩大，比如我们将其修改为5，如下图所示，我们会发现规划算法收敛的速度会加快，不过拓展出的随机树变得稀疏，规划出的路径也会相对更加直来直去一点。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现当我们缩小步长限制，比如我们将其设置为1，如下图所示，我们会发现规划算法收敛的速度会稍微变慢一点，不过还是在接受范围内。并且随机树变得更加茂密，规划出的路径也相对更加接近光滑。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现假如我们进一步缩小步长限制，比如我们将其设置为0.5，这时我们会明显的感受到规划速度大大降低，已经超出合理的范围。最终的随机树相当的茂密，基本上已经探索完地图中的所有自由区域。不过这种效果是以牺牲效率为代价的。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现那么有没有既不牺牲效率，也能做到规划路径比较光滑的方法呢？有的，双树RRT就可以。下面，我们仍然保持着0.5的步长限制，但是这次我们使用双树RRT进行规划。如下图所示。我们发现，不但规划的效率没有下降，甚至还有提升。所以通过实践我们知道，相同的条件下，双树RRT的效率要比单树RRT高出许多。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现那么让我们换张更大的地图来看看，RRT在大地图中的表现如何？首先是单树RRT，设置步长限制为2.5，我们可以虽然成功得规划出路径，但是却花费20秒的时间，这明显是令人无法接受的规划效率。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现
那么轮到双树RRT，同样的设置步长限制为2.5，结果如下图所示，与单树RRT相比，双树RRT简直是太优秀了，在规划出比较理想的路径的前提下，仅仅花费了1.4秒。双树RRT完胜无疑。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现

3. RRT的不足

RRT和PRM一样属于基于概率的规划算法，这类算法都有个致命的短板，就是面临狭长的通道时很难找到有效路径，就算最终找到了也是会花费相当长的时间。如下图所示，单树RRT在面临狭长通道时，虽然找到了有效路径，但是花费了86秒，这完全是不可接受的。
运动规划入门 | 4. 白话RRT，从原理到Matlab实现
好了，RRT的部分我大概就讲到这里，问我要代码的小伙伴可以自己多试试看不同的地图和参数配置，甚至可以自己创建地图进行试验，这会有效地帮助你搞懂RRT。下一篇我将讲解运动规划入门系列的最后一个算法——人工势场法。咱们下次再见。 推荐阅读： 运动规划入门 | 1. 白话Dijkstra，从原理到Matlab实现运动规划入门 | 2. 白话A*，从原理到Matlab实现运动规划入门 | 3. 白话PRM，从原理到Matlab实现