书接上回,上一次我们讲完了Dijkstra,如果小伙伴们有印象的话,肯定还记得在上一篇的文末,我们提到了Dijkstra的致命缺点:处理大地图时效率低下。那么今天我们就来看看Dijkstra的近亲A*究竟做出了哪些改变来解决效率问题?

1. A*原理详解
我们知道,Dijkstra之所以效率低下,就是因为Dijkstra对地图里所有的相邻栅格都“一视同仁”,所以Dijkstra在运行的时候会花费很多精力去访问一些对规划结果没有贡献的节点。形象地说,Dijkstra就像是洪水一般四处扩散,缺乏目的性。而A*恰恰就是在目的性这一点上下了功夫,在我看来A*就是一波有目的、有梦想的洪水,它知道自己该往哪个地方流。 那么A*究竟是做了什么改变而变得高效的呢?
1.1 路径规划中的贪婪算法
由于实际上A*可以看成Dijkstra和贪婪算法的结合体,使得A*同时具备了Dijkstra和贪婪算法的优势。所谓贪婪算法没有一种固定的形式,算法的重点在于你贪婪的策略。在路径规划中的贪婪算法说白了就是:每次都朝着四周离终点最近的点移动(离终点的总代价值最小)。那么显而易见的,在贪婪算法在做路径规划时,每次考虑的都是当前位置的四周范围内的最优解,这是一种局部最优解,贪婪算法的优势在于可以迅速地找到终点完成规划,缺点是:很可能规划出来的并不是全局最优的路径,某种意义上来说,这是一种牺牲“精度”换取“速度”的规划方式。 下图是贪婪算法在20*20的地图中的表现:

1.2 A*的“智慧”来源:评价函数和启发函数
前面我们说了A*可以看作Dijkstar和贪婪算法的结合,Dijkstar在规划中注重的是当前节点到起点的总代价值,也称后退代价。而贪婪算法注重的是当前节点到终点的总代价值,也称前进代价。那么所谓的结合实际上就是说,A*同时考虑到了后退代价和前进代价。从表达式上看就是:后退代价+前进代价 下式中的g(n)表示当前节点的后退代价,h(n)表示当前节点的前进代价,但是更多人称h(n)为启发函数。而右边的f(n)则被称为评价函数。
 评价函数将会计算当前节点的后退、前进代价的总和,这个数值表明这个节点在规划中的重要程度,或者说是优先考虑程度。在A*中节点的评价函数返回值越小就表明该节点的重要性越高,或者说更应该被优先考虑。A*算法在每轮迭代中都会选择未完成列表中评价函数返回值最小的节点。那么有了评价函数的介入,A*算法看待节点的态度就不再是“一视同仁”了,根据评价函数的结果,A*会将节点分“三六九等”,那么A*就获得了目的性。 我们先来琢磨琢磨Dijkstar的代价函数为什么不具备目的性,老规矩举个例子:在一个九宫格里,假设中心的那一格是起点,那么对整个九宫格运行代价函数后得到的结果就会像下面这样:起点的代价值为0,因为只需要移动一次能到达所以跟起点相邻的4个方格的代价值是1,以此类推,四个角上的代价值就为2。
评价函数将会计算当前节点的后退、前进代价的总和,这个数值表明这个节点在规划中的重要程度,或者说是优先考虑程度。在A*中节点的评价函数返回值越小就表明该节点的重要性越高,或者说更应该被优先考虑。A*算法在每轮迭代中都会选择未完成列表中评价函数返回值最小的节点。那么有了评价函数的介入,A*算法看待节点的态度就不再是“一视同仁”了,根据评价函数的结果,A*会将节点分“三六九等”,那么A*就获得了目的性。 我们先来琢磨琢磨Dijkstar的代价函数为什么不具备目的性,老规矩举个例子:在一个九宫格里,假设中心的那一格是起点,那么对整个九宫格运行代价函数后得到的结果就会像下面这样:起点的代价值为0,因为只需要移动一次能到达所以跟起点相邻的4个方格的代价值是1,以此类推,四个角上的代价值就为2。
 上面这个例子乍一看好像没啥问题,但是当我们将网格扩大到5*5,并且加入了终点G,如下图所示:右下角的节点作为终点,如果按照Dijkstar的代价函数来看的话,其余三个角上的节点相对起点的代价是一样的,都是4。但是考虑到搜索算法的效率,这三个角的方向都是在远离终点G,简直就是“南辕北辙”。朝着这三个方向进行的探索都是在做无用功。这便是Dijkstar的盲目性,由于其盲目性,所以Dijkstar会做很多无用的搜索。但是并不是说这种盲目的搜索是不可取的。盲目搜索的优点在于:Dijkstar可以尽可能多地探索地图,当我们修改终点的位置时,Dijkstar不需要做过多的重复规划,由于先前第一次探索的时候已经完成了带有父节点的代价地图,在实际地图没有发生改变的前提下,生成的代价地图是可以重复使用的。
上面这个例子乍一看好像没啥问题,但是当我们将网格扩大到5*5,并且加入了终点G,如下图所示:右下角的节点作为终点,如果按照Dijkstar的代价函数来看的话,其余三个角上的节点相对起点的代价是一样的,都是4。但是考虑到搜索算法的效率,这三个角的方向都是在远离终点G,简直就是“南辕北辙”。朝着这三个方向进行的探索都是在做无用功。这便是Dijkstar的盲目性,由于其盲目性,所以Dijkstar会做很多无用的搜索。但是并不是说这种盲目的搜索是不可取的。盲目搜索的优点在于:Dijkstar可以尽可能多地探索地图,当我们修改终点的位置时,Dijkstar不需要做过多的重复规划,由于先前第一次探索的时候已经完成了带有父节点的代价地图,在实际地图没有发生改变的前提下,生成的代价地图是可以重复使用的。
 但是为了满足大部分情况下我们更希望规划算法能够快速地给出特定的解的需求,于是A*的评级函数便有了其用武之地。
但是为了满足大部分情况下我们更希望规划算法能够快速地给出特定的解的需求,于是A*的评级函数便有了其用武之地。
1.3 启发函数的选择
和盲目搜索相对的,这种有目的性的搜索被称为启发式搜索(Heuristically Search)。启发式搜索存在的意义就是:缩小搜索范围,提高搜索的目的性,提高效率。 前面说过A*是Dijkstar和贪婪算法的组合,那么g(n)和h(n)占f(n)的比重就决定了A*的行为,假如h(n)占更高的比重,那么A*就表现得更像贪婪算法,假如g(n)占更高的比例,那么A*就表现得更像Dijkstar。 举个极端例子,当我们设h(n) = 0的时候,A*便会退化回Dijkstar。当我们设g(n) = 0时,A*就变成了贪婪算法。所以权衡好g(n)和h(n)的比例是至关重要的。我们一般会通过修改启发函数来调节A*的行为。那怎么样才算好的行为呢?好的规划行为无法两个要点:能找到最优解的前提下,效率最高。比如Dijkstar的规划行为就属于能找到最优解,但是效率不高。而贪婪算法恰好相反,效率高,但是不能保证找到最优解。 题外话:A算法和A*算法的区别,其实两者的评价函数形式均为:f(n) = g(n)+h(n),只不过A*是选择了“最优启发函数“的A算法。也就是说A*是A算法中”最优的“。所以A*是A算法的子集。但是一般情况下我们并不会刻意区分这两者,所以全文就统称为A*。 那么我们该如何得到一个合适的启发函数呢?(注:讨论“启发函数的选择”的这部分内容会涉及比较多的概念问题,总体来说比较绕。如果是只想了解A*如何实现的小伙伴,可以跳过这部分内容,从曼哈顿距离开始看) 一个好的启发函数需要满足几个约束:1.满足可纳性;2.满足一致性;3.目标状态的h(n) = 0
1.4 什么叫可纳性?
如果从起点到终点有一条路径,而搜索算法一定能在有限步内终止并找到一个最优解(代价最低),则这个搜索算法称为可采纳的(可纳)。A*算法要满足可纳性是有条件的,它需要满足:
 其中h*(n)表示最小前进代价,也就是当前节点到终点的最小距离(比如直线距离)。该不等式表明了一个事实:启发函数不能高估当前节点到终点的距离。
其中h*(n)表示最小前进代价,也就是当前节点到终点的最小距离(比如直线距离)。该不等式表明了一个事实:启发函数不能高估当前节点到终点的距离。
1.5 什么叫一致性?
一致性的意思就是:对每个节点n的任意后继节点n’,节点n的估计前进代价不大于从n到n’的总代价与n’的估计前进代价之和。其表达式如下,其中c(n,n’)表示两点之间的代价值。
 实际上这就是一道三角不等式:
实际上这就是一道三角不等式:
 该表达式可以通过下面的化简,变为f(n’) >= f(n),所以一致性也就是在表示一个约束:当前节点的总评价值不大于任意后继节点的总评价值。
该表达式可以通过下面的化简,变为f(n’) >= f(n),所以一致性也就是在表示一个约束:当前节点的总评价值不大于任意后继节点的总评价值。
 在A*中,只要h(n)满足一致性,那么h(n)必然满足可纳性。证明过程过于繁琐,此处就不再赘述。小伙伴们就把它看成一个定理吧。
在A*中,只要h(n)满足一致性,那么h(n)必然满足可纳性。证明过程过于繁琐,此处就不再赘述。小伙伴们就把它看成一个定理吧。
1.6 曼哈顿距离(Manhattan Distance)
在只允许上下左右移动的栅格地图中,我们一般使用曼哈顿距离作为启发函数,用于估算两点之间的距离。因为曼哈顿距离即满足一致性和“h(goal) = 0“的特性,而且算法简单,计算成本低。 曼哈顿距离的定义式如下,其实就是将两点的坐标差值相加。
![]() 那么使用曼哈顿距离作为启发函数,根据上面我们举例的5*5地图,对其执行评分函数将会是什么结果呢?下图的等式右边第一个矩阵表示的是g(n)(后退代价)的各个值,第二个矩阵表示的是曼哈顿距离(前进代价)的各个值,两个矩阵相加后得到等式右边的矩阵f(n),可以看到,f(n)的矩阵的值带有很强的方向性,当我们使用这个矩阵作为代价地图,在此基础上执行类似之前Dijkstar一样的的迭代的话,其实就是A*了。
那么使用曼哈顿距离作为启发函数,根据上面我们举例的5*5地图,对其执行评分函数将会是什么结果呢?下图的等式右边第一个矩阵表示的是g(n)(后退代价)的各个值,第二个矩阵表示的是曼哈顿距离(前进代价)的各个值,两个矩阵相加后得到等式右边的矩阵f(n),可以看到,f(n)的矩阵的值带有很强的方向性,当我们使用这个矩阵作为代价地图,在此基础上执行类似之前Dijkstar一样的的迭代的话,其实就是A*了。

1.7 其他启发函数
当然,启发函数不单单曼哈顿距离一种,常见的还有欧式距离、切比雪夫距离等等。 欧式距离就是我们最熟悉的两点间距离的计算方式:
![]() 而切比雪夫距离就是找出x,y坐标差值中较大的那个值:
而切比雪夫距离就是找出x,y坐标差值中较大的那个值:
![]()
2. A*的Matlab实现
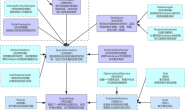
上一篇中我们已经讲过如何构建网络占用地图,所以这里就不再赘述。我们直接来看看算法流程图
2.1 流程图
 对比上一篇的Dijkstar流程,可以发现两者是非常相似的,A*只是多了一个NodeFList用于储存节点的评价函数值F和Heuristic函数用于计算启发值,并且在每轮迭代中A*都是挑选未完成列表中F值最小的节点作为CurrentNode。
对比上一篇的Dijkstar流程,可以发现两者是非常相似的,A*只是多了一个NodeFList用于储存节点的评价函数值F和Heuristic函数用于计算启发值,并且在每轮迭代中A*都是挑选未完成列表中F值最小的节点作为CurrentNode。
2.2 启发函数的实现
实际上按照前面提到过的启发函数来看,像曼哈顿距离、欧式距离这些,其实都不难用Matlab实现出来。但是我在实现代码的时候加入了一个之前没有提到过参数scale。之前说过,启发值h(n)占评价值的比例不同会导致不同的A*行为。而这个额外加入的参数就是用来放缩我们的启发值,从而调节启发值的比例的。后面我们会为小伙伴们对比不同scale值导致的不同现象。

2.3 核心代码
老样子,需要完整matlab源码的小伙伴可以在评论区找我要,我发邮箱。
while true
[min_node_cost, current_node_index] = min(node_f_list(:));
if(min_node_cost == inf || current_node_index == destination_index)
plan_succeeded = true;
break;
end
node_f_list(current_node_index) = inf;
map(current_node_index) = Finished;
[x,y] = ind2sub(MapSize, current_node_index);
for k = 0:3 % four direction
if(k == 0)
adjacent_node = [x-1,y];
elseif (k == 1)
adjacent_node = [x+1,y];
elseif (k == 2)
adjacent_node = [x,y-1];
elseif(k == 3)
adjacent_node = [x,y+1];
end
if((adjacent_node(1) > 0 && adjacent_node(1) <= MapSize(1)) && (adjacent_node(2) > 0 && adjacent_node(2) <= MapSize(2))) % make sure the adjacent_node don't exceeds the map
if(map(adjacent_node(1),adjacent_node(2)) ~= Obstacle && map(adjacent_node(1),adjacent_node(2)) ~= Finished)
if(node_g_list(adjacent_node(1),adjacent_node(2)) > min_node_cost + 1 )
node_g_list(adjacent_node(1),adjacent_node(2)) = node_g_list(current_node_index) + 1;
node_f_list(adjacent_node(1),adjacent_node(2)) = node_g_list(adjacent_node(1),adjacent_node(2)) + Heuristic(adjacent_node, destination, Heuristic_scale);
if(map(adjacent_node(1),adjacent_node(2)) == Origin)
parent_list(adjacent_node(1),adjacent_node(2)) = 0; % Set the parent 0 if adjacent_node is the origin.
else
parent_list(adjacent_node(1),adjacent_node(2)) = current_node_index; %Set the parent current_node_index
end
if(map(adjacent_node(1),adjacent_node(2)) ~= Unfinished)
map(adjacent_node(1),adjacent_node(2)) = Unfinished; % Mark the adjacent_node as unfinished
end
end
end
end
end
end
2.4 效果对比
这是A*在20*20的地图上的效果
 这是Dijkstra在20*20的地图上的效果
这是Dijkstra在20*20的地图上的效果
 从返回的结果上看,两者都找到了最优的路径,路径长30。但是从迭代次数上来看,Dijkstra迭代了235次,但是A*只迭代了153次。从动画上也能看到,和Dijkstra的盲目搜索不同,A*向外扩展到一定位置就停止了蔓延。因此可以看出,A*的效率更高。
从返回的结果上看,两者都找到了最优的路径,路径长30。但是从迭代次数上来看,Dijkstra迭代了235次,但是A*只迭代了153次。从动画上也能看到,和Dijkstra的盲目搜索不同,A*向外扩展到一定位置就停止了蔓延。因此可以看出,A*的效率更高。
 现在,让我们换个大一点的地图看看效果。我们换成100*100的地图 A*的表现如下:
现在,让我们换个大一点的地图看看效果。我们换成100*100的地图 A*的表现如下:
 Dijkstra的表现如下:
Dijkstra的表现如下:
 可见,在更大的地图上的表现差异更加明显了,两者都找到相同的最优路径,A*经历了1938次迭代,但是Dijkstra却经历了4235次迭代。从两者扩展的节点数量来看,Dijkstra也比A*多扩展了许多节点。
可见,在更大的地图上的表现差异更加明显了,两者都找到相同的最优路径,A*经历了1938次迭代,但是Dijkstra却经历了4235次迭代。从两者扩展的节点数量来看,Dijkstra也比A*多扩展了许多节点。
 我记得前面我还提了一嘴,说不同的启发值占比会导致A*不同的行为。那这里我们多做一个启发值不同的效果对比: 在代码中的A*函数里,这个Heuristic_scale就是用来设置启发函数的scale值的。我们原本的代码将其设置为1。也就是说启发值等于曼哈顿距离。
我记得前面我还提了一嘴,说不同的启发值占比会导致A*不同的行为。那这里我们多做一个启发值不同的效果对比: 在代码中的A*函数里,这个Heuristic_scale就是用来设置启发函数的scale值的。我们原本的代码将其设置为1。也就是说启发值等于曼哈顿距离。
 假设我们将其增大一点点,就一点点,比如0.001。那么会得到什么样的效果呢?
假设我们将其增大一点点,就一点点,比如0.001。那么会得到什么样的效果呢?
![]() Emmmmmm, 好像也没什么太大的区别。
Emmmmmm, 好像也没什么太大的区别。
 让我们看看迭代次数和路径长度:
让我们看看迭代次数和路径长度:
![]() 可以看见相比上一次的1938次,这一回好像确实是稍微减少了迭代次数,不过路径长度变成了134,明显不是最优路径。这些特征确实满足了贪婪算法的特性。但是权衡之下,似乎得不偿失。等等,别急,让我们来看看另一种情况。 现在,我们将终点改为[100,100],也就是在最右下角。这回再看看会不会产生不同的情况。 哦豁,这就太不一样了。可以看到,算法的探索行为几乎就是直奔目的地而去的
可以看见相比上一次的1938次,这一回好像确实是稍微减少了迭代次数,不过路径长度变成了134,明显不是最优路径。这些特征确实满足了贪婪算法的特性。但是权衡之下,似乎得不偿失。等等,别急,让我们来看看另一种情况。 现在,我们将终点改为[100,100],也就是在最右下角。这回再看看会不会产生不同的情况。 哦豁,这就太不一样了。可以看到,算法的探索行为几乎就是直奔目的地而去的
 从迭代次数上看,仅仅只有199次,路径长度跟Dijkstra的结果一样也是198。
从迭代次数上看,仅仅只有199次,路径长度跟Dijkstra的结果一样也是198。
![]() 当我们多改变几次终点值后,我们会发现这时的A*确实表现得更像贪婪算法。迭代次数减少,但是不一定每次都能找到最优路径。所以当我们增大启发值的占比,其实就是在提高算法的运行效率,但是降低了准确度。这却决于实际的场景,毕竟不是每个场景都要求路径最优,有些情况下更希望算法快速地找到一条比较好的路径,而不是花较高的计算成本来找到最优路径。 至于降低启发值的比例会产生什么样的结果,那就是启发值的占比越低,A*表现得就越像Dijkstra。虽然会找到最优解,但是也会花费更多的计算成本。 经过以上对比以后,我在想,A*经历几千次迭代才后能在100*100的地图中完成规划,虽然现代计算机硬件已经能支持这样级别的运算,在我们的matlab演示代码中,假如关闭动画显示,我们会发现即使是几千次的迭代,实际上也只花费了几百毫秒的时间。但是那假如我们用的地图更大A*是否还能胜任呢?有没有别的办法,可以不需要对地图的栅格一一遍历就能完成路径规划呢? 答案是有,下一篇,我们就来说说PRM(概率路线图),这种方法不需要对地图的栅格进行一一遍历就能完成规划。
当我们多改变几次终点值后,我们会发现这时的A*确实表现得更像贪婪算法。迭代次数减少,但是不一定每次都能找到最优路径。所以当我们增大启发值的占比,其实就是在提高算法的运行效率,但是降低了准确度。这却决于实际的场景,毕竟不是每个场景都要求路径最优,有些情况下更希望算法快速地找到一条比较好的路径,而不是花较高的计算成本来找到最优路径。 至于降低启发值的比例会产生什么样的结果,那就是启发值的占比越低,A*表现得就越像Dijkstra。虽然会找到最优解,但是也会花费更多的计算成本。 经过以上对比以后,我在想,A*经历几千次迭代才后能在100*100的地图中完成规划,虽然现代计算机硬件已经能支持这样级别的运算,在我们的matlab演示代码中,假如关闭动画显示,我们会发现即使是几千次的迭代,实际上也只花费了几百毫秒的时间。但是那假如我们用的地图更大A*是否还能胜任呢?有没有别的办法,可以不需要对地图的栅格一一遍历就能完成路径规划呢? 答案是有,下一篇,我们就来说说PRM(概率路线图),这种方法不需要对地图的栅格进行一一遍历就能完成规划。