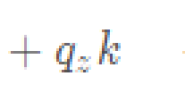刚体动力学基础学习

1 符号

：刚体上某个质量微元对固定点O的位置矢径：刚体上一点P对固定点O的位置矢径：刚体上某个质量微元对基点P的位置矢径：刚体质心C对P的位置矢径：质量：点k的速度：角速度：点k的加速度：动量：关于点k的绝对动量矩：关于点k的相对动量矩：合外力：对点k的合外力矩

2 动量

3 动量矩

动量矩的这部分内容相对复杂，因为要分成好多种情况进行讨论。分别是：

对固定点的动量矩
对动点的绝对动量矩
对动点的相对动量矩

首先，要对动点和固定点做区分。动点就是在动坐标系上的点，固定点就是在固定坐标系（或者说是惯性系）下的点。其次，要对绝对动量矩和相对动量矩做区分。动量矩的计算公式是矢径和速度的乘积的积分，所谓绝对动量矩就是用绝对速度求解的动量矩，而相对动量矩就是用相对速度（相对动坐标系的速度）来求解的动量矩。由此可知，对固定点求动量矩，都没有绝对动量矩和相对动量矩的说法，因为对固定点都是绝对动量矩。而对于动点求动量矩，就有二者的区分。另外，特别值得注意的是，动点中有一个点，非常特殊，那就是质心，它是占据有非常特殊地位的一个动点。对于质心而言，绝对动量矩和相对动量矩是相等的。而对于一般的动点，这一条完全不成立。

3.1 对固定点O的动量矩

3.2 对动点P的相对动量矩

公式(3-1)右端的第三项，实际上就是刚体在相对P点平动坐标系运动中对P点的动量矩。它的意思就是说，假设有一个坐标系固连在P点上，这个坐标系相对固定点O在平动，然后，计算刚体相对于P点的动量矩。因此，上式也可以写成：

3.3 对动点P的绝对动量矩

公式(3-1)右端的第二和第三项，实际上是刚体对P点的绝对动量矩。而上式又可以写作：

3.4 对质心C的相对动量矩和绝对动量矩

相对动量矩刚体在绝对运动（相对于固定点O的运动）中，对刚体质心的动量矩，等于，刚体在相对运动（相对基点P的运动）中对质心的动量矩。即：

3.5 固定点的动量矩与对动点的动量矩之间的关系

对固定点的动量矩与对动点P的绝对动量矩的关系为：当P点就是C点时，

4 动量定理

上式便是牛顿动力学方程。

5 动量矩定理

5.1 动量矩基本定理（无需证明的）

刚体对固定点O的动量矩定理：刚体对质心的动量矩定理：

5.2 刚体对动点的绝对动量矩定理

首先申明，刚体对动点的绝对动量矩就是前文推导的 $G_P$ 。对动点的绝对动量矩的意思就是，对平移坐标系的原点求动量矩，但是求解时用的是绝对速度。所以，所以求导，其中，代表了刚体所受的外力系对动点P的主矩，它的定义为：最终，刚体对动点的绝对动量矩定理的表达形式为：

5.3 刚体对动点的相对动量矩定理

首先申明，刚体对动点的相对动量矩就是前文推导的 $G_{P''}$ 。对动点的相对动量矩的意思就是，对平移坐标系的原点求动量矩，但是求解时用的是相对速度。求导：又因为，，其中 $J_{P}$ 是一个张量在某组坐标系（基）下的坐标矩阵，它的取值和基的选取非常相关。如果 $J_{P}$ 表示在固定坐标系下，那么由于刚体的旋转， $J_{P}$ 的取值时时刻刻都会发生变化。而如果 $J_{P}$ 表示在与刚体固连的动坐标系下，那么其取值可以为一个常量。另外，必须注意，当 $J_{P}$ 表示在动坐标系下时，此时公式中相应的也是表示在动坐标系下的。所以：所以，若把公式 (5-9) 带入公式 (5-8) ，可得：若 P 点就是质心，则，由公式 (5-10)，可得：上式便是鼎鼎大名的欧拉动力学方程了。最终，刚体对动点的相对动量矩定理的表达形式为：