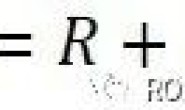从零手写VIO——（三）基于优化的 IMU 与视觉信息融合（下篇）

接着上篇：从零手写VIO——（三）基于优化的 IMU 与视觉信息融合（上篇）   再次说明一下，本博客目前只是我在看深蓝时记录的，当然会有很多 PPT 上的内容，加上一点自己学的时候的理解，或者补全没有写全的推导，目的是能够留下一个电子形式的资料，直接目的是留给自己之后反复查看。每次视频我都是一点点啃下去的，属实对我这种本科生并不友好（本科大牛请绕路），所有内容都是一点点用 LaTeX 打上去的，不是截图搬运。也感谢贺博、高博及深蓝的精美课程！

VIO 残差函数的构建

带权重的残差计算

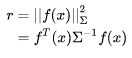
其中， 
 服从高斯分布，协方差为 
 。

1. 协方差  用来 归一化，多传感器融合  单位不统一，如：PnP的误差方程的单位是像素，即实际像素点和理论像素点之间的误差；IMU 的误差单位为米(  )和 度(  )。
2. 权重。协方差越小代表数据越集中，  就越大，代表权重越高。如说残差方程相差大，协方差大，说明可能存在误匹配 – 坏值，那么  较小权重低。

基于滑动窗口的 VIO Bundle Adjustment

高博的视觉SLAM十四讲里，对滑动窗口理论没有做过多的讲述，从上式(19) 
 是先验，是后入数据时扔掉的前数据转化成的part， 
 和 
 是新窗口内数据的残差方程， 
 是上篇提到的鲁棒核函数。 定义优化的系统状态量：

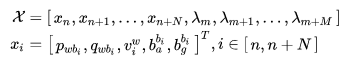
1.  是  时刻 IMU 在惯性坐标系中的位置，姿态，速度，IMU 机体坐标系下加速度和角速度的偏置量估计。  是  时刻的观测点。
2.  分别是滑动窗口里机体状态量和观测路标的起始时刻。N 代表状态量在窗口内的关键帧数，M 是窗口内所有关键帧观测到的路标点数。

视觉重投影误差

一个特征点在 归一化相机坐标系 下的估计值和观测值的差。

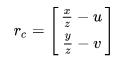
其中，待估计的状态量为特征点的三维空间坐标 
 ，观测值 
 为特征在相机归一化平面的坐标。

逆深度参数化 Inverse Depth Parametrization

特征点在 归一化相机坐标系 与 相机坐标系 下的坐标关系为：

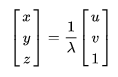
其中 
 称为 逆深度^[1]。逆深度更容易表示无穷远处的点，当 
 ，可以用来表示无穷远处；且 
 更接近正态分布。在实际应用中，逆深度也具有更好的数值稳定性。     特征点逆深度在第 
 帧中初始化得到，在第 
 帧又被观测到，预测其在第 
 中的坐标为：

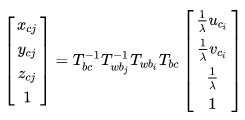
这里的变换矩阵其实就是先从一帧的相机坐标系 
 这帧的 IMU body 坐标系 
 World 坐标系 
 另一帧的 body 坐标系 
 另一帧的相机坐标系。第一帧的 u-v 是可以通过亚像素的方法配准的，故用 
 这一个参数表示第一帧的观测。 视觉重投影误差为：

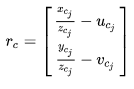
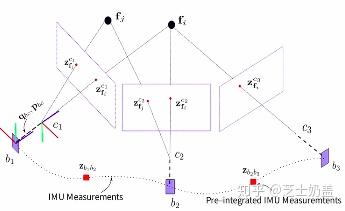
IMU 测量值积分

IMU 的真实值 
 ，测量值为 
 ，则有：

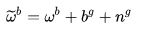
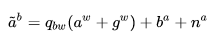
上标 
 表示 gyroscope， 
 表示 Accelerometer， 
 表示世界坐标系 world， 
 表示imu 机体坐标系 body。 PVQ 对时间的导数可写成：

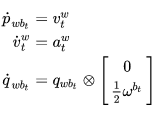
从第 
 时刻的 PVQ 对 IMU 的测量值进行积分得到第 j 时刻的 PVQ：

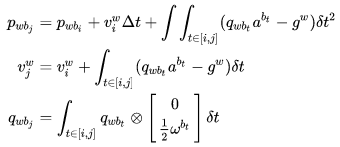
目标→解决：每次 
 优化更新，都需要对之后时间线上的重新积分。

IMU 预积分^[2]

积分模型到预积分模型：

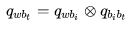
那么，PVQ 积分公式中的积分项则变成相对于第 
 时刻的姿态，而不是相对于世界坐标系的姿态：

预积分量

预积分量仅仅跟 IMU 测量值有关，它将一段时间内的 IMU 数据直接积分起来就得到了 预积分量：

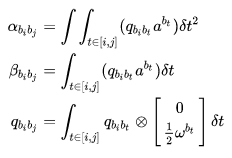
PVQ 的积分公式：

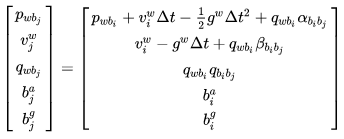
认为短时间内的 bias 是不变的。 预积分误差：一段时间内 IMU 构建的预计分量做为测量值，对两时刻之间的状态量进行约束。

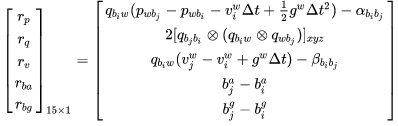
 表示只取四元数的虚部 
 组成的三维向量， 
 是预积分估计值，四元数 
 的结果是 
 即

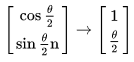
代表转角 
 接近0，这里只取出 xyz 就是取出旋转角的残差乘以2得到 
 。等号左边每项都是一个三维度的共十五维，除四元数外，其他项均为 j 处世界坐标系下的真值减去 预积分以外的估计值（通过 
 从世界坐标系转换到 i 坐标系），再在 i 坐标系下与预积分值相减得到预积分误差。

预积分的离散形式

这里使用中值法，即两个相邻时刻 k 到 k+1 的位姿用两个时刻的测量值 
 的平均值计算：

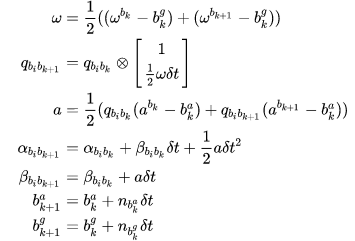
测量数据 
 都减去了 bias 可以用过标定获得，bias 服从随机游走，故有了后两个式子。随后的目的是 如何求算离散形式的多个 IMU 数据积分形成的累计预积分量的协方差。

协方差的传递 Covariance Propagation

已知 
 ，则有 
 ，证明其实在之前提过：

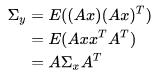
假设已知相邻时刻误差的线性传递方程：

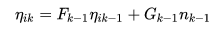
比如：状态量误差为 
 ，测量噪声为 
 。 误差的传递由两部分组成：当前时刻的误差传递给下一时刻，当前时刻测量噪声传递给下一刻。 协方差矩阵可以通过递推得到：

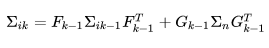
其中， 
 是测量噪声的协方差矩阵，方差从 i 时刻开始递推， 
 ；Allan 方差计算出了测量噪声的方差量级。

状态误差线性递推公式的推导

1. 基于一阶泰勒展开的误差递推方程。
2. 基于误差随时间变化的递推方程。

基于一阶泰勒展开的误差递推方程

令状态量为 
 ，其中，真值为 
 ，误差为 
 。另外，输入量 
 的噪声为 
 。 非线性系统 
 的状态误差的线性递推关系如下：

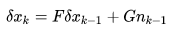
其中， 
 是状态量 
 对状态量 
 的雅可比矩阵， 
 是状态量 
 对输入量 
 的雅可比矩阵。 对非线性状态方程进行一阶泰勒展开有：

基于误差随时间变化的递推方程

如果能够推导状态误差随时间变化的导数关系，如：

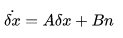
则误差状态的传递方程为：

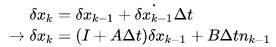
对比两个方法有：

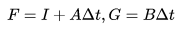
为什么会有误差随时间变化这种方法?

因为 VIO 系统中已知状态的导数和状态之间的转移矩阵。比如说速度的导数与状态量之间的关系：

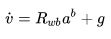
那么就可以推导速度的误差和状态误差之间的关系，再每一项上都加上各自的误差就有：

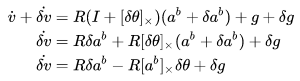
预积分的误差递推公式推导

白噪声的值不能像 bias 一样估计，故白噪声不能像 bias 一样减去。 下面误差的 Jacobian 是，在递推公式（ 
 用了中值法）等式左右分别对偏导分子分母加上一个误差 
 后求出该 Jacobian。对于 
 是用 
 。

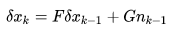
用前面一阶泰勒展开的推导方式，我们希望推导出误差的递推公式：

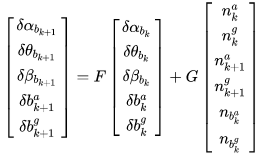
 为两个时刻间的协方差传递矩阵， 
 表示各时刻的误差。 
。

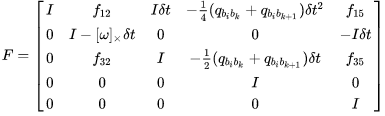
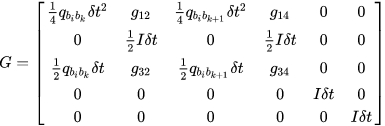
其中系数为：

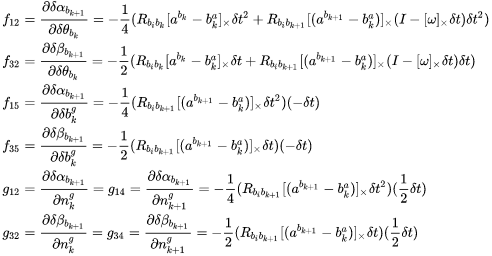
对部分项做详细推导↓对于导数中与变量无关的项省去：

 对各状态量的雅可比推导，  第三行

速度预计分量 
 的递推计算形式：

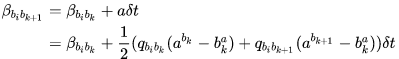
 ：对上一时刻速度预积分量的 Jacobian

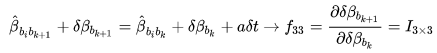
 ：对角度预积分量的 Jacobian

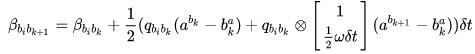
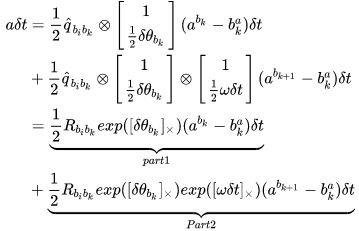
Part 1 对应的雅可比为：

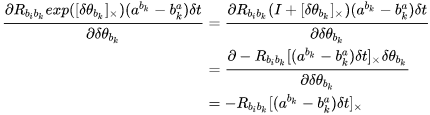
Part 2 对应的雅可比为：

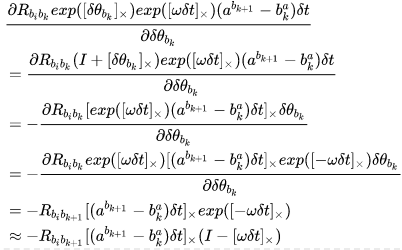
合起来就是(47)中的 
 。

 ：速度预积分量对 k 时刻角速度 bias 的 Jacobian

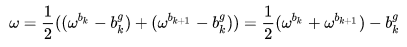
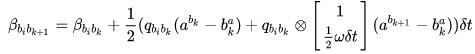
就有了这样的雅可比推导过程：

旋转预计分量的 Jacobian，  第二行

旋转预积分递推公式：

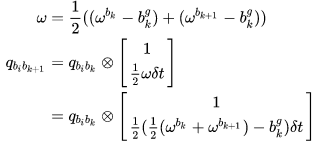
 ：前一时刻的旋转误差  如何影响当前旋转误差 

假设两个时刻的真值是 
 ，不考虑受到角速度 bias 的影响，两时刻的增量

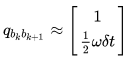
三元组四元数相乘有如下性质（其实就是伴随性质，在李群李代数证明过）：

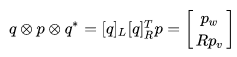
其中 
 是和 
 对应的旋转矩阵， 
 为 
 的实部， 
 为 
 的虚部。

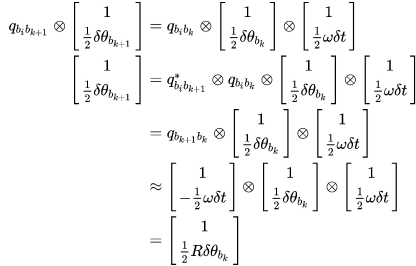
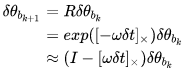
故第 k+1 时刻的旋转预积分的误差相对于第 k 时刻的 Jacobian 为：

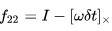
残差 Jacobian 的推导

归一化平面视觉残差为：

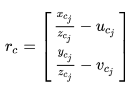
对于第 i 帧中的特征点，它投影到第 j 帧相机坐标系下的值为：

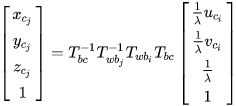
写成三维坐标形式为：

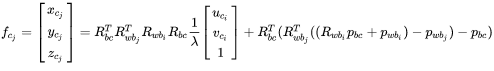
这里的 
 是因为是从 
 的变化，是相反的。此处把旋转和平移拆解开，平移部分为， 
 的平移部分 
 会经过三次旋转加平移的变换直到 j 的 camera 坐标系下。 变量定义：

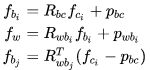
Jacobian 对状态量，外参和逆深度求导：

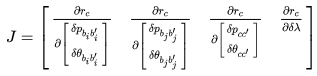
step 1：先求error对 
 的导数，与 《视觉SLAM十四讲》不同之处是这里在归一化平面。

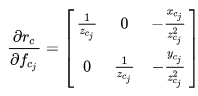
step 2：  对 i 时刻的状态量求导。 对位移求导↓

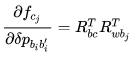
对角度求导↓

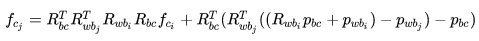
只保留与 
 有关的项：

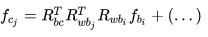
这里的 
 即 i 坐标系下的坐标转换到 world 坐标系下。 Jacobian 为：

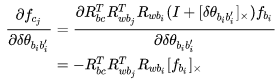
step 3：  对 j 时刻的状态量求导。 对位移求导↓

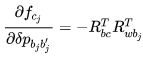
负号的原因可以看式(65)， 
 在式中与 
 相乘，求导固然结果如此。 对角度求导↓

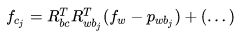
Jacobian 为：

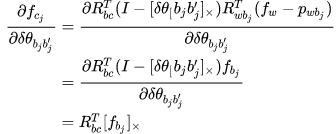
step 4：对 imu 与相机之间的外参求导。 就是对两传感器之间的旋转和平移求导。 对位移求导↓

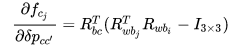
对角度求导↓Jacobian 为：

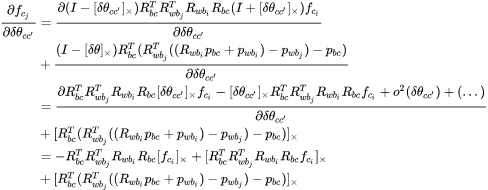
step 5：视觉误差对特征逆深度的求导

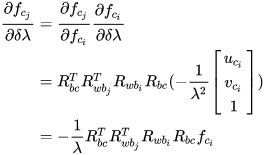
IMU 误差相对于优化变量的 Jacobian

预积分误差如下图↓ 这里的误差和上部分提到的误差是两码事，我是这么理解的，上部分提到的误差是通过递推 k 到 k+1 时刻间的误差传递；这里的误差是预积分误差，是求出的两时刻的位置、速度与真实值之间的误差。

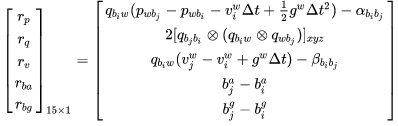
上式中， 
 是估计值。 由于 i 时刻的 bias 相关的预积分计算是通过迭代一步一步累计递推的，很复杂。故预积分量直接在 i 时刻的 bias 附近用一阶泰勒展开近似。

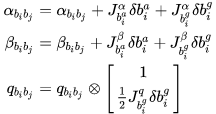
对  进行推导：

• 对 i 时刻位移：由于与位移无关，故 Jacobian 为 0；
• 对 i 时刻旋转：

• 对 i 时刻速度：  ；
• 对 i 时刻的加速度 bias 的 Jacobian，由于加速度只影响预积分，故  。

对  进行推导：

• 对 i 时刻姿态求导：

这里的 
 就是提取 xyz 虚部，乘以系数 2，就是微小转动的 
 ，前面有解释。然而(76)式中对分子几个四元数 
 ，取共轭后的 
 等于在整个式子前加负号。

• 对 i 时刻陀螺仪偏置  ：

式中对角速度 bias 求 Jacobian，用一阶泰勒展开的形式，最后矩阵内 1 对 
 求导为 0。    

参考

1. ^Civera J , Davison A J , J. M Martínez Montiel. Inverse depth parametrization for monocular SLAM[J]. IEEE Transactions on Robotics, 2008, 24(5):932-945. http://web.mit.edu/2.166/www/handouts/davison_tro2008.pdf
2. ^Forster C , Carlone L , Dellaert F , et al. On-Manifold Preintegration for Real-Time Visual–Inertial Odometry[J]. ieee transactions on robotics, 2017, 33(1):1-21. https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=7557075