开心洋葱 , 版权所有丨如未注明 , 均为原创丨未经授权请勿修改 , 转载请注明SLAM14讲学习笔记(四)视觉里程计(特征点法)和重难点总结!
SLAM14讲学习笔记(四)视觉里程计(特征点法)和重难点总结

-
从零手写VIO——(三)基于优化的 IMU 与视觉信息融合(上篇) -
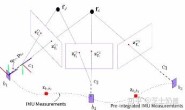
从零手写VIO——(三)基于优化的 IMU 与视觉信息融合(下篇) -
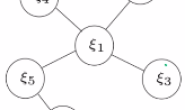
从零手写VIO——(四)基于滑动窗口算法的 VIO 系统:可观性和一致性(下)滑动窗口算法 -

从零手写VIO——(四)基于滑动窗口算法的 VIO 系统:可观性和一致性(上)舒尔补
- 从零手写VIO——(五)视觉前端 Frontend
- 从零手写VIO——(六)VINS 初始化和 VIO 系统
- 【SLAM】VINS-MONO解析——综述
- 【SLAM】VINS-MONO解析——基于vins-mono的双目slam系统开发
- 【SLAM】VINS-MONO解析——初始化(理论部分)
- 【SLAM】VINS-MONO解析——初始化(代码部分)
- 【SLAM】VINS-MONO解析——后端优化(理论部分)
- 【SLAM】VINS-MONO解析——后端优化(代码部分)
- 【SLAM】VINS-MONO解析——sliding window
- 【SLAM】VINS-MONO解析——IMU预积分
- SLAM14讲学习笔记(九)单目稠密重建、深度滤波器详解与补充
- SLAM14讲学习笔记(十二)ch9设计前端(代码详述)
- 从网络到分布式-负载均衡
- 潮汐表表v3.0 全新升级
- Error when trying to install SageAttention – distutils._msvccompiler has no attribute ‘_get_vc_env’
- Java 16最前沿技术——ZGC
