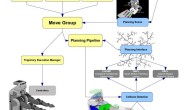
引言
实际应用中,我们也会经常使用到直线轨迹,然而(5)中讲的三次多项式并不能满足我们的直线轨迹。然而如果单纯地使用直线轨迹,线段间的转折点会让速度不连续,如何又能使用直线轨迹又能满足速度连续呢?在这里引出一次多项式(直线)与二次多项式的结合使用。
目录
直线轨迹规划
多段直线轨迹规划
符号的设定与相关公式
公式
影响加速度的因素
补充说明
相关例题
直线轨迹规划
一般使用一次多项式(即直线方程式)与二次多项式一起使用,二次多项式的目的是为整个线段提供等加速与等减速,由此达到速度连续无断层的目的。 其实之前也讲过,轨迹规划核心就是拟合线嘛。 三次多项式需要参数 ,因此在三次多项式的轨迹规划中,求解
是核心。 所以我认为直线轨迹规划的核心有两个: 一个是要知道速度 v——求解直线段的关键参数。一个是要知道加速度 a——求解曲线段的关键参数。

统一符号 整个线段时刻区间为 [
,
] 。 其中
和以前一样是角度位置,[
点]代表速度,即对
求导。[
点点]代表加速度,即对[
点]求导。
衔接了一次多项式和二次多项式,为直线轨迹的起点对应时刻,可作为“中间点”看待。
为直线轨迹的终点对应时刻,可作为“中间点”看待。
为直线轨迹经历时间的一半,也是整个线段的一半。
由图中的等式,我们和之前一样,当达到中间点的时刻 需要将中间点前后的式子带入
并使之相等,就能得到连续的速度。
 纯直线轨迹规划、直线轨迹规划、三次多项式轨迹规划 拟合直线轨迹的区别
纯直线轨迹规划、直线轨迹规划、三次多项式轨迹规划 拟合直线轨迹的区别  或许就有人纳闷了,使用直线轨迹规划,第二列的加速度也“不连续”啊,其实真实上电控手臂的加速度变化会通过电产生一个扭力达到变化,其实电压也是一个从零慢慢变化的过程,但是电比机械响应得快,所以这样的加速度的需求是可以满足的。
或许就有人纳闷了,使用直线轨迹规划,第二列的加速度也“不连续”啊,其实真实上电控手臂的加速度变化会通过电产生一个扭力达到变化,其实电压也是一个从零慢慢变化的过程,但是电比机械响应得快,所以这样的加速度的需求是可以满足的。
上面那个例子是为了更好地说明举出的特殊例子——头尾两端速度都是0。实际上一般我们在做轨迹规划时常采用的是多段的直曲结合表示直线的轨迹规划,而多段中的许多中间段的头尾速度都不为0,那怎么做呢?看下面。
多段直线轨迹规划
符号的设定与相关公式
统一符号(1)中间多段的符号设定

是中间点,
与中间点
中夹着“半个曲线(属于
的二次多项式)+一整个直线+半个曲线”(属于
的二次多项式)。
代表中间点
的二次多项式段(曲线段)的时间
代表中间点
到
的直线段的时间
代表中间点
到
(包括曲线和直线)的时间差
 其中sgn()的作用是确定方向,正负号。这些公式都是初高中的物理学学过的了….不多说。
其中sgn()的作用是确定方向,正负号。这些公式都是初高中的物理学学过的了….不多说。
统一符号(2)头尾段的符号设定
 【头段】将起点后移一段时间(一般是曲线段时间的一半),前面导入一段圆滑的曲线连接。起点就会到达的新的位置(即图中所示
【头段】将起点后移一段时间(一般是曲线段时间的一半),前面导入一段圆滑的曲线连接。起点就会到达的新的位置(即图中所示点)。此时就能将“起点”当作“中间点”了,更好地方便运算。定义完以后就能列出物理等式了,如上图。

【尾段】将终点前移一段时间,后面导入一段圆滑的曲线连接。终就会到达的新的位置(即图中所示
点)。此时就能将“终点”当作“中间点”了,更好地方便运算。定义完以后列出物理等式,如上图。
公式

影响加速度的因素
 这个涉及到了动力学,稍微了解下就行。
这个涉及到了动力学,稍微了解下就行。
补充说明
(1) 规划完后,会发现原来我们设定的中间点,都到达不了怎么办?  在必须通过的中间点附近添加一些假的中间点,这样我们设定的中间点会落在直线段上,且不管二次式轨迹如何规划都影响不到我们直线的轨迹。
在必须通过的中间点附近添加一些假的中间点,这样我们设定的中间点会落在直线段上,且不管二次式轨迹如何规划都影响不到我们直线的轨迹。  (2)为什么常在Cartesian space下做直线规划? 除了更直观以外。如果我们在Joint space下做“等速段”的直线轨迹运动,想想好像是可行的,等角速嘛。但是实际上Joint space和Actuator space息息相关,表面上Joint space是等角速,其实实际上我们还要考虑它关节内部的速度等等,麻烦。
(2)为什么常在Cartesian space下做直线规划? 除了更直观以外。如果我们在Joint space下做“等速段”的直线轨迹运动,想想好像是可行的,等角速嘛。但是实际上Joint space和Actuator space息息相关,表面上Joint space是等角速,其实实际上我们还要考虑它关节内部的速度等等,麻烦。
相关例题
仍然使用以前的例子,使用直线轨迹规划求解。(Cartesian下解题)  解析题目,题目给出了4个坐标点的三个关键量
解析题目,题目给出了4个坐标点的三个关键量 、
、
, 要求在Cartesian下用直线轨迹规划方法解题,也就是要求我们分别求出这三个关键量的连续的直线轨迹。 与之前三次多项式轨迹规划不同的是,本章直线轨迹规划(曲+直)在意的是加速度、速度公式,有了加速度的物理公式,才能规划出曲线部分在图上的表达,有了速度的物理公式,才能规划出直线在图上的表达。所以第一步: (1)连接需求(题目)规定要到达的点,知道大概的轨迹图
 其中蓝色速度
其中蓝色速度代表直线部分,绿色加速度
代表曲线部分,红色为需要到的点。 可以看到,蓝色线段与绿色线段一共有7段。 (2)先求出需求点和每段的速度、再求出加速度 注:每段加速段的时长为0.5秒
 上文【统一符号】中已经定义过,头尾点需要内移了加速段的一半时间,所以时长如红色部分所示要减去(0.5 / 2) (3)使用求出的速度和加速度,构建轨迹的连续方程式。 讲直线轨迹规划的时候已经给过公式了:
上文【统一符号】中已经定义过,头尾点需要内移了加速段的一半时间,所以时长如红色部分所示要减去(0.5 / 2) (3)使用求出的速度和加速度,构建轨迹的连续方程式。 讲直线轨迹规划的时候已经给过公式了:  结合公式,我们就能求出题目要求的
结合公式,我们就能求出题目要求的 轴的七段方程式:

轴的轨迹方程式已经求出,剩下两个
、
也是类似的求法,在此不列出。 最终得到的三条轨迹就是:
 (4)检验可行性 求出答案后最好IK逆向算出驱动转角,再FK顺向得到移动位置,看看该轨迹在现实中是否可行。
(4)检验可行性 求出答案后最好IK逆向算出驱动转角,再FK顺向得到移动位置,看看该轨迹在现实中是否可行。  感谢:课程内容和PPT来自台湾林沛群教授的《机器人学》!
感谢:课程内容和PPT来自台湾林沛群教授的《机器人学》!