经典机器学习系列(十二)【学习排序】

排序学习一般被认为是supervised learning中的一个特例，谈到supervised learning其loss function一般表示为如下形式：  
  supervised learning中我们首先想到的是Regression 和 Classification，其loss function分别表示为如下形式：  

• Regression

  Regression经常以mean-square-error构建loss function  
 

• Classification

Classification常以cross-entropy构建loss function  
  上述的loss function都是建立在一个instance个体本身上面，而不是一群instance上面。

Learning to Rank Problem

  而这个Learning to Rank就比较有意思，输入是 a set of instances:  
  输出是a rank list of these instances：  
  其中下标表示的是排序位置，比如r 1 = 1，表示x 1 排在第一个位置，r 1 = 2 ，表示x 2​排在第一个位置。   真实标签就是a correct ranking of these instances：  
  Learning to Rank就是在一系列instances下面做supervised learning

Information Retrieval

  Information Retrieval更广泛的意思是说，我们有一个user。他有一个 information need ，希望在a collection of information items里面通过索引、排序等方法，然后返回一些相关的items给用户。

A Typical Application: Web Search Engines

 
  当我们每天在做检索的时候其实也在反馈，他们的rank应该如何去做会更好一些。   在上述过程中有Two key stages索引检索相关的候选文档和排序这些文档。  

• Retrieve the candidate documents
• Rank the retrieved documents

  而Rank the retrieved documents我们可以用Learning to Rank的方式来做。由于Learning to Rank不可能对所有的documents排序，因此有第一步索引。  

• Overview Diagram of Information Retrieval

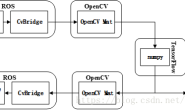
  整个Web Search Engines其大体的核心步骤可描述为下图所示：  
 

1. Inverted Index

  给一个文档，需要知道有哪些关键词  

2. Relevance Model

  当用户输入一个query之后，依据Inverted Index我们可以找到一些候选集，  

3. Query Expansion & Relevance feedback model

  这里所做的是对Query的一个扩充，比如拿前十名的文档对关键词进行扩充，能够使得Query更加全面，排序结果更加稳定，返回更好的user的information need。  

4. Ranking document

  最后去做Learning to Rank的这个model，使得排序结果更好，更好的服务于用户。

Webpage Ranking

  整个learning to rank的framework如下图所示：  
  当user输入query时，第一步是获得Retrieved Items，之后基于这个Retrieved Items做ranking model，然后输出Ranked List of Documents。

Learning to Rank

Model Perspectiv

  目前大部分learning to rank的工作建模为两方面的问题， query-document以feature的形式建模出来。  

• Each instance (e.g. query-document pair) is represented with a list of features

有时候的query是非常离奇的，搜索引擎从来没有见过，因此我们需要将query映射到feature space上面。  

• Discriminative training

这里主要是当给一个query-document pair我们需要Estimate the relevance，也就是一个打分函数f θ f_{\theta}fθ​：  
  之后需要基于the estimation去Rank the documents。基于这个rank与真正的rank做loss function，再train就可以了。   总结一下在Learning to Rank的framework下面：  

• 输入：features of query and documents 像Query, document, and combination features这些
• 输出：the documents ranked by a scoring function y i = f θ ( x i ) y_{i} = f_{\theta}(x_{i})yi​=fθ​(xi​)
• 目标函数是一些relevance of the ranking list，像Evaluation metrics: NDCG, MAP, MRR…这些。
• 训练数据： the query-doc features and relevance ratings，数据格式如下图所示：

 
可以看出query已经被转成了数字化的feature了。这样的话即使没有见过这个query，没有见过这个documents，我们依然能够在feature space上面去建模这个点。 在Learning to Rank上面我们其实是学习scoring function。

Learning to Rank Approaches

微软亚洲研究院副院长Tie-Yan Liu在2011的《 Learning to Rank for Information Retrieval》中将Learning to Rank大致分为三类：Pointwise、Pairwise、Listwise  

• Tie-Yan Liu. Learning to Rank for Information Retrieval. Springer 2011.

Pointwise

<code class="has-numbering">- Predict the absolute relevance (e.g. RMSE) 
</code>

  Pointwise方法中对单个instance打分，问题就变成了一个回归问题：  
  这是最简单的Learning to Rank，这里有一个问题，Point Accuracy != Ranking Accuracy。Same square error might lead to different rankings，如下图所示：  
  也就是说最后所作的优化并不是rank上的优化。  

Pairwise

<code class="has-numbering">- Predict the ranking of a document pair (e.g. AUC) 
</code>

  对于排序问题，如果scoring functionf θ f_{\theta}fθ​改变一点点，那是很有可能导致你最终的排序结果不会发生改变。当loss function建立在排序上面的话，那么你的loss function对函数参数求导就会等于0。   正是由于这个原因，我们无法对scoring function求导。解决办法如下图所示：  
 
 
 

• Burges, Christopher JC, Robert Ragno, and Quoc Viet Le. “Learning to rank with nonsmoothcost functions.”NIPS. Vol. 6. 2006

  Pairwise Approaches也存在一些问题，如：Each document pair is regarded with the same importance。但是很多时候，用户对前面几个页面的rank是要更加关注一点，因此Same pair-level error but different list-level error就需要注意。  
 
 
 

Listwise

• Predict the ranking of a document list (e.g. Cross Entropy)

Listwise Approaches

• Training loss is directly built based on the difference between the prediction list and the ground truth list
• Straightforward target •Directly optimize the ranking evaluation measures
• Complex model

• Cao, Zhe, et al. “Learning to rank: from pairwise approach to listwise approach.”Proceedings of the 24th international conference on Machine learning. ACM, 2007.

• Burges, Christopher JC, Robert Ragno, and Quoc Viet Le. “Learning to rank with nonsmooth cost functions.”NIPS. Vol. 6. 2006.

Summary of Learning to Rank