在学校听的华为云ModelArts的公开课。其实大部分都是在讲深度学习的入门,也稍微介绍了一下华为云的这个深度学习平台。
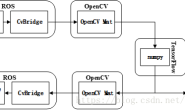
1. 华为云ModelArts开发平台简介
华为云ModelArts是化而为最新推出的AI云平台。可以看一下挂网的介绍——什么是ModelArts。和tensorflow与pytorch这样的平台相比,这个平台的优势在于:免安装环境,注册就能上手;更适合小白上手训练——当然这是要收费的,定价可以参考这里。
结合我自己的学习经验,在学习深度学习的时候,很多小案例都可以在本地跑完,但是一但涉及到卷积等复杂的深度学习模型,用自己的电脑跑就会很久很久,效率很低。之前都是用的学校的超算中心申请服务来跑,如果没有这些条件的话,华为ModelArts平台算是一个还不错的选择。ModelArts平台提供了深度学习从数据标注、训练、部署的全生命周期的一站式服务。新手可以直接在平台上体验华为内部的训练算法。在体验“自动学习”项目时,可以使用华为免费的GPU服务,但是排队估计要久一点。
2. 深度学习简介
2.1 深度学习概论
AI与传统的计算机科学有什么不同
传统的计算机技术是执行人类预定义好的命令,AI则是让计算机有了学习的过程。
专用人工智能和通用人工智能
现在很多成熟的人工智能基本都是专用的人工智能,比如AlphaGo、图像识别。然而这些领域的人工智能并不能像人脑一样做到举一反三,如果要进行新的任务,则要进行重新的训练,非常地消耗资源,因此,有学者提出,meta learning(元学习)是未来实现从专用人工智能到通用人工智能的关键。
人工智能发展的三大要素
- (1)Big Data——有标签的高质量数据。数据是深度学习的“粮食”,虽然现在对数据的存储能力大幅地提升了,但是深度学习更需要的是有标签的高质量数据。
- (2)Computing——深度学习的“加速器”。进行深度学习训练任务是需要GPU来进行矩阵运算加速的,因为大型的深度学习模型是需要进行大量的矩阵运算。
- (3)Algorithm——算法。机器学习和深度学习本质上都是寻找一组最优的函数映射关系。
深度学习算法
深度学习算法的框架主要由深度神经网络组成。
- CNN——图像处理
- RNN——序列数据的处理
- GAN——对抗生成网络——现在比较火的网络。
深度学习研究前沿
(1)Explainable AI(可解释的AI)。深度神经网络是一种黑盒机制,是一种不能解释的方法。然而,在深度学习网络不断优化、任务化的今天,我们可能更加关心一个问题——为什么深度学习网络是有效的?对于Explainable AI的了解可以看一下这篇文章——初探Explainable AI。
(2)Network Depression(网络压缩)。
(3)Adversial Attack(对抗攻击)。
(4)Meta Learning(元学习)
2.2 神经网络与BP反向传播算法
感知机与多层感知机
神经网络是由多层感知机(MLP,Multilayer Perceptron)发展来的。感知机(Perceptron)是线性分类的二分类模型,主要用来解决二分类问题,对感知机的了解可以看一下这篇文章——深度学习入门-感知机,讲的非常详细。
单层感知机可以解决与门/或门/非门的逻辑问题(线性可分问题),多层感知机比单层感知机增加了决策平面,可以解决异或问题(线性不可分问题)。相比于多层感知机,随着宽度和深度的拓展,就形成了我们今天使用的神经网络。
神经网络及相关概念
神经网络是深度学习的有效方法之一。第一步就是选择一个网络结构,接着,找到训练方法,评价网络性能,最后选择表现最好的那组参数。这就是使用神经网路进行深度学习的基本步骤。根据神经网络中不同神经元之间的连接方式,就形成了我们目前使用的一系列深度神经网络模型。
神经网络的基本单位是神经元。神经元主要的作用就是进行信息的传递,接受信号的输入,激活后,向后输出。权重是神经元之间连线上的值,表示改节点输出对后面神经元的影响程度。对于同样的网络架构,不同的权重得到的输出是不一样的,权重是通过网络训练和学习得到的。对于每个神经元来说,其进行的运算就是加权求和之后加上一个阈值/偏置量(bias),并使用激活函数进行计算。权重和偏置量都是需要不断训练和学习的。

图片引用自神经网络详解(基本完成)
激活函数给神经网络加入非线性变换,可以让神经网络更好地解决复杂的问题,它可以控制哪些信息传递、哪些信息不传递。隐藏层常用的激活函数可以看这篇文章——常用激活函数(激励函数)理解与总结。需要注意的是,神经网络的激活函数一定要是非线性的。
3. 神经网络训练
推荐阅读:
神经网络BP反向传播算法原理和详细推导流程
详解神经网络的前向传播和反向传播
Neural Network and Deep Learning
在训练过程中,我们需要计算预测值和真实值之间的误差,也就是通常所说的loss function(损失函数),用以评价损失函数的好坏。关于loss function可以看一下神经网络系列之三 — 损失函数。损失函数越小,就说明我们的神经网络预测的越准确,因此,我们就是希望能够找到损失函数的最小值。
求极值的问题自然而然就可以想到求导。我们计算出损失函数在各个方向(针对各个参数)的梯度,就可以得到函数下降最快的方向,并进行反向传播(也就是我们说的梯度下降法),通过不断地优化损失函数,就可以得到一个更准确的神经网络——这就是我们所说的训练和学习的过程。
当然,在使用梯度下降法进行反向传播的过程中,很容易出现以下问题和挑战:
第一,极小值问题
在进行梯度下降的时候,很容易会陷入“局部最优(local optimal)”的陷阱。其次,每次优化的步长也决定着我们进行梯度下降法的效果和效率。——关于这一部分建议看一下吴恩达老师的机器学习课程,会理解的 比较清楚。第二,鞍点问题
一般来说,越复杂的网络越难进入“局部最优”的陷阱,因为复杂的网络优化的方向特别多,不容易“掉进坑里”。但是,鞍点问题是复杂网络需要注意的问题。在鞍点处,损失函数的梯度在一个方向上是极小值,另一个方向上是极大值。关于鞍点问题解决,这个回答——神经网络迭代中如何最有效地逃离鞍点?——里的一张图还蛮有意思的。第三,梯度消失与梯度爆炸
推荐阅读:神经网络梯度消失与梯度爆炸
在模型实践的过程中,发现小批量梯度下降(Mini-Batch Gradient Descent, MBGD)的效果更好,所以在批量训练(Batch Training)中,需要注意一下一些概念——神经网络中Epoch、Iteration、Batchsize相关理解和说明。在训练过程中,为了防止过拟合,通常会在训练中dropout一些神经元(深度学习中Dropout原理解析),但是需要注意的是在验证时是不需要dropout的。