这是我见过讲解最详细最通俗易懂的决策树（一）

基本流程

  我们在这篇文章没有公式，我们只谈决策树里面跟大家简单的介绍了决策树是个啥东西。今天我们将深入的介绍一下决策树。   首先决策树是一类常见的机器学习方法，以二分类任务为例。我们希望从给定的数据集中学习一个模型用来对新的示例进行分类。   如下图所示：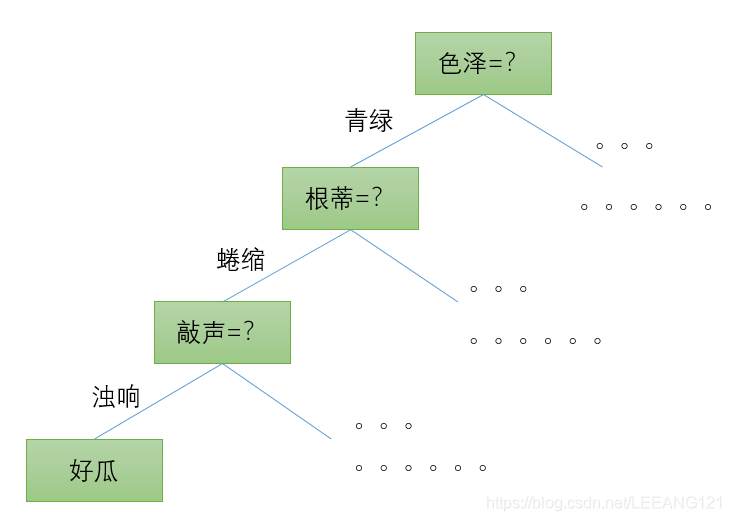  
  这是一个我们选择西瓜时，判断该瓜是否为好瓜的决策过程。   那么什么是决策？ 决策就是我们判断西瓜是不是好西瓜，这就是我们的决策，好西瓜我们就买，不是好西瓜就不买。   那么我们通过什么决策？ 通过一系列西瓜特有的属性，例如这个西瓜的色泽如何？根蒂如何？敲击声音如何？等等等等。   决策树学习目的是为了产生一颗泛化能力强、可以处理未见示例的决策树。   显然，决策树是一个递归过程。在决策树算法中，有三种情况会导致递归返回：   1，当所有结点包含的样本属性全属于同一类别，无需划分； 2，当前属性集为空，或者所有样本在所有属性上取值相同，无法划分； 3，当前结点包含的样本集合为空，不能划分。   那么问题来了，上述三种情况具体是什么含义呢？ 这里我用下面的西瓜选型图跟大家解释一下（个人理解）  
  搞明白上面的基本概念之后，我们面临的下一个问题就是：  

如何划分选择

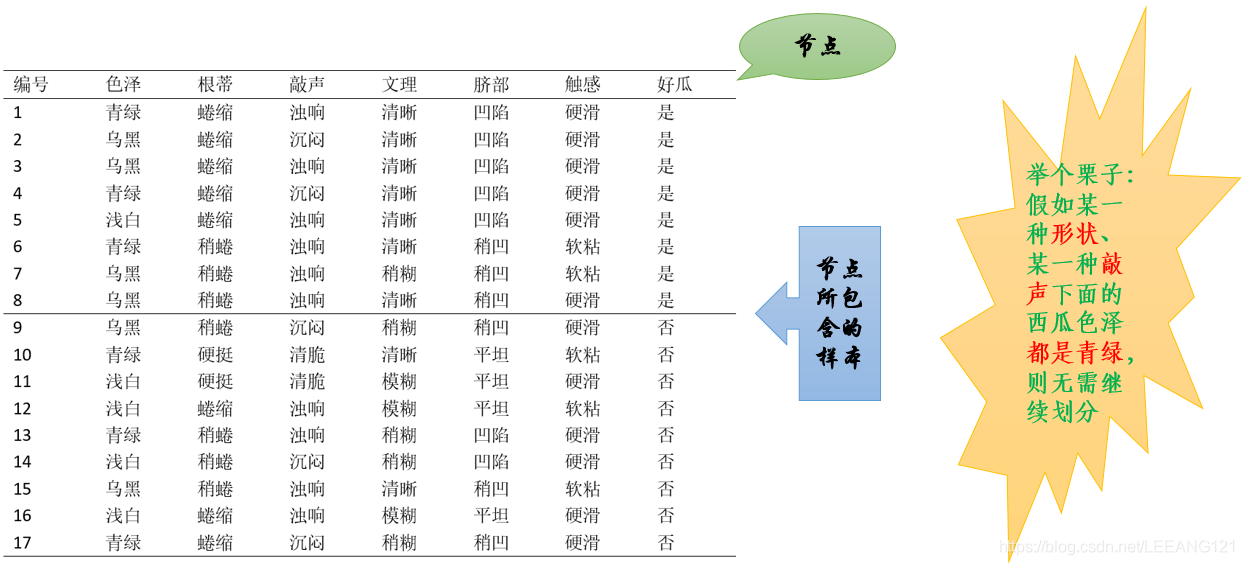
  从开篇第一幅图及上面的后续介绍，我们可以发现，决策过程其实就是不断划分的过程。我们是希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的’纯度‘会越来越高。   信息增益   大家看到这个名词的时候不用慌张，其实仔细想一想，仅从字面意思也不难理解，信息增益的意思就是指某条信息对整体的增幅情况。简单可以理解为该信息的   权重。 在研究权重之前，我们先回到上面那个纯度的问题上，通常我们会用‘信息熵’来度量样本集合的纯度，熵这个词大家还有没有印象？如果忘记了可以参考我的一篇博文啥也不会，照样看懂交叉熵损失函数，这里有介绍熵的概念及公式。   当然这里我们也会简单进行一下说明：假定当前样本集合D 中的第k 类样本所占比例为p k(k=1,2,3,…|y|,则D 的信息熵为  
 
 
 
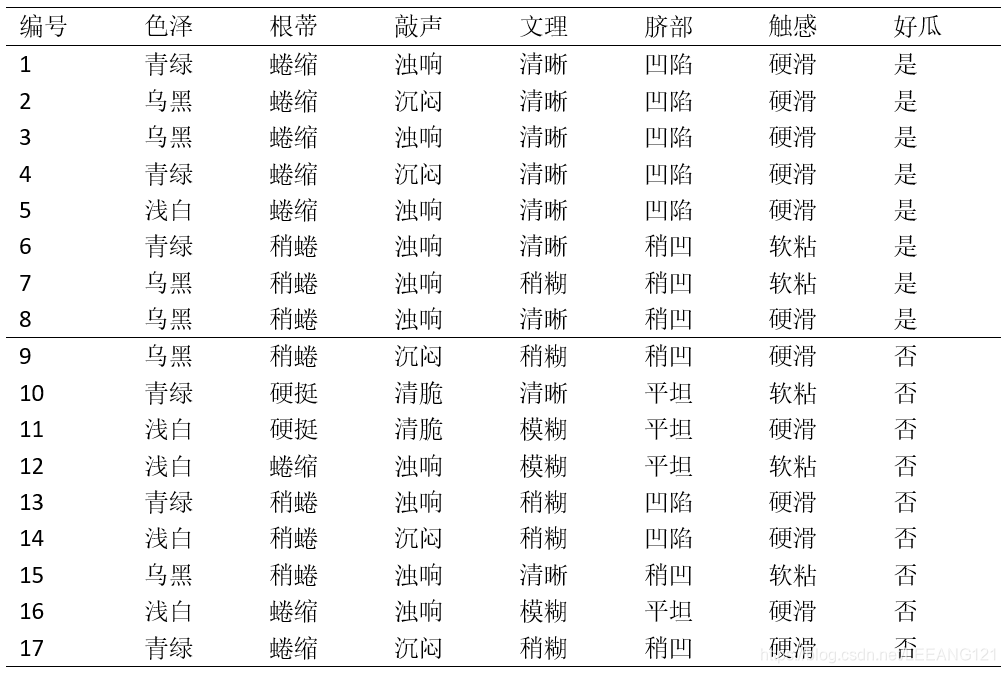
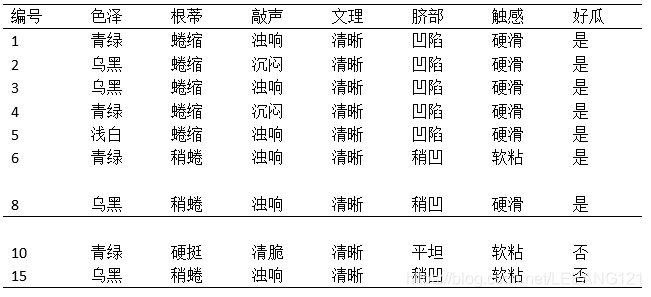
  现在我们来计算每个属性的信息增益。   我们以属性’色泽‘为例，它有三个可能的取值（青绿、乌黑、浅白）。在我们利用这个色泽属性对D进行划分的时候，可以得到三个子集，我们把这三个子集分别记为：   D1(色泽=青绿） D2(色泽=乌黑） D3(色泽=浅白）  
 
  很明显，属性’纹理‘的信息增益最大，于是它被选择用来划分属性。 下图显示了基于‘纹理’对根节点进行划分的结果，各分支结点所包含的样例子集显示在结点中。  
  接下来，决策树算法将对每个分支结点做仅一步的划分。我们以上图分支结点（‘纹理=清晰’）为例，该结点包含的样例集合D 1 中有编号为{1，2，3，4，5，6，8，10，15}的9个样例，这9个样例又分别包含了属性集合{色泽、根蒂、敲声、脐部、触感}。基于D 1计算出各属性的信息增益为：   Gain(D1,色泽)=0.043 G a i n ( D 1 , 根 蒂 ) = 0.458  G a i n ( D 1 , 敲 声 ) = 0.331  G a i n ( D 1 , 脐 部 ) = 0.458 G a i n ( D 1 , 触 感 ) = 0.458   tips上面的计算过程还是要在简单说一下：  
  1，当我们以D 1中有编号为{1，2，3，4，5，6，8，10，15}的9个样例为集合时，我们可以假定西瓜数据集就剩下这9行（上述这9个数字所代表的属性行） 2，本来的E n t ( D )中的分母由17变成了9，分子分别为7和2 3，此时计算得到的E n t ( D ) = 0.764  4，色泽=青绿的正概率为3 / 4、色泽=乌黑的正概率为3 / 4，色泽=浅白的正概率为100  5，以上为此时的计算说明。   ‘根蒂’、‘脐部’、‘触感’3个属性均取得了最大的信息增益，可以任选其中之一作为划分属性。类似的，对每个分支结点进行上述操作，最终得到决策树如下：  
   

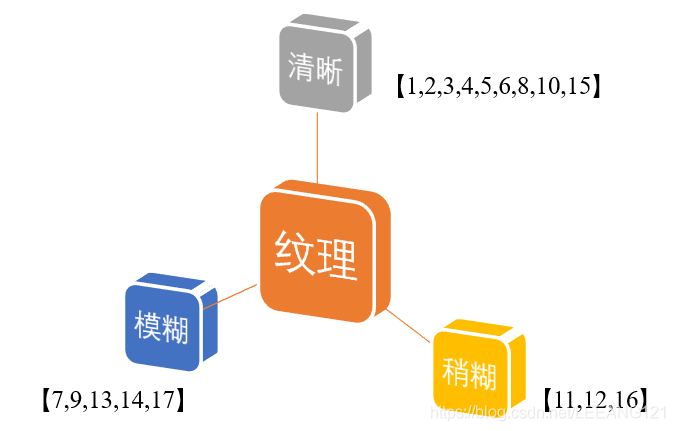
总结

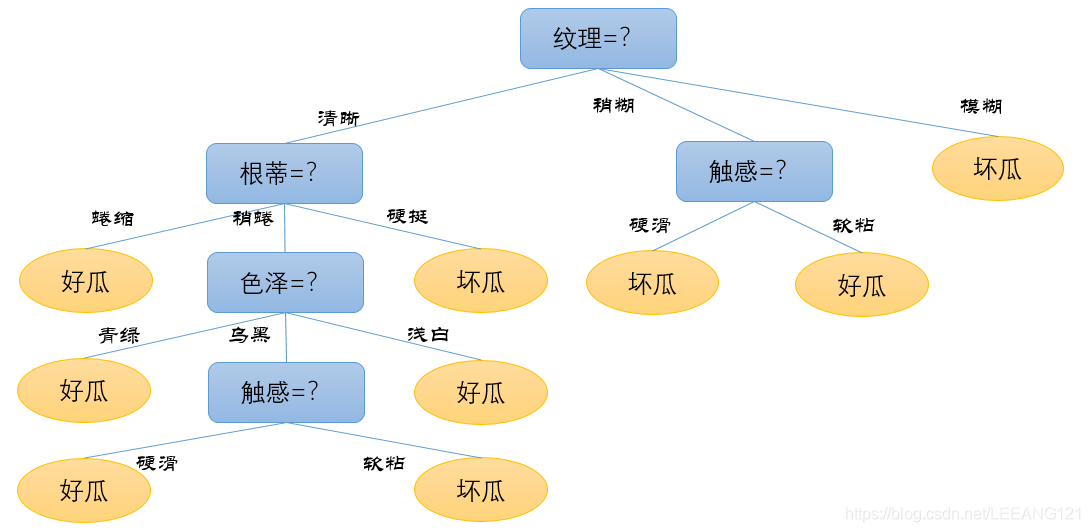
以上就是决策树以及如何划分结点的详细说明，下一节我们会重点介绍： 增益率 基尼指数 剪枝处理 预剪枝 后剪枝 以上所有内容均来自周志华的《机器学习》，以及一点个人的心得。 这里还要感谢郭老师的大力支持。