【机器人学】机器人开源项目KDL源码学习：（2）牛顿拉普森迭代法求机器人的数值解

对于串联机器人来说，求逆解的难度要大于求正解，市面上的工业机器人一般是利用的是利用解析法求封闭解，机器人有封闭解是有条件的—Pieper法则。另一种求逆解的方法是利用迭代法求数值解，适用于不满足Pieper法则的构型，特别适用于运动学冗余的机械臂。

KDL提供了3种逆解方法：（1）纯牛顿拉普森迭代法；（2）关节限位的牛顿法；（3）基于LM的方法。其中（1）和（2）几乎是相同的，只是在迭代求解的时候加了一个关节限位，下边简单介绍KDL中第（1）种方法。

可以将求机器人逆解的问题看成是一个求多元非线性方程组的问题，而牛顿拉普森迭代法就是求这个问题的一个可选的方法。

第一步：方程组可写成如下形式：

（1）

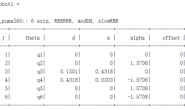
表示机械臂的正运动学函数，操作空间共有m个自由度。

表示机械臂具有n个关节。如果n>m则机械臂运动学冗余。

表示机械臂末端的在操作空间维度的目标点。

第二步：求取雅克比矩阵：

（2）

第三步：迭代法求解下一个关节的位置：

（3）

其中：

表示当前的误差（目标点的位姿-当前点的位姿），这与（1）式是相反的，所以（3）式的等式后是加号，这么写是为了要和KDL中的程序一致。

逆矩阵使用雅克比矩阵的伪逆矩阵，KDL代码中并没有单独的伪逆矩阵的求解器，而是直接求的伪逆矩阵和误差的乘积。

KDL中的代码（orocos_kdl\src\chainiksolverpos_nr）：

int ChainIkSolverPos_NR::CartToJnt(const JntArray& q_init, const Frame& p_in, JntArray& q_out)
    {
        if(q_init.rows() != nj || q_out.rows() != nj)
            return (error = E_SIZE_MISMATCH);
 
            q_out = q_init;
 
            unsigned int i;
            for(i=0;i<maxiter;i++){
                if (E_NOERROR > fksolver.JntToCart(q_out,f) )
                    return (error = E_FKSOLVERPOS_FAILED);
                delta_twist = diff(f,p_in);
                const int rc = iksolver.CartToJnt(q_out,delta_twist,delta_q);
                if (E_NOERROR > rc)
                    return (error = E_IKSOLVER_FAILED);
                // we chose to continue if the child solver returned a positive
                // "error", which may simply indicate a degraded solution
                
                Add(q_out,delta_q,q_out);
                //
                if(Equal(delta_twist,Twist::Zero(),eps))
                    // converged, but possibly with a degraded solution
                    return (rc > E_NOERROR ? E_DEGRADED : E_NOERROR);
            }
            return (error = E_MAX_ITERATIONS_EXCEEDED);        // failed to converge
    }

关键代码段说明：

 delta_twist = diff(f,p_in);//这行代码表示求取的是Err项

const int rc = iksolver.CartToJnt(q_out,delta_twist,delta_q);//这行求的是上述第三步等号后边的第二项，把值传给了 delta_q

Add(q_out,delta_q,q_out);//这行进行的是第三步的运算，更新的值为 q_out,再进行下一次迭代，逐渐逼近真实解

KDL中的雅克比矩阵是几何雅克比矩阵，原理可看《机器人学：建模、规划和控制》这本教材，KDL中是以一种很巧妙的方式求出来，具体可看：【机器人学】机器人开源项目KDL源码学习：（5）KDL如何求解几何雅克比矩阵