3D图像信息复原

给定一个立方体模型，通过深度相机将模型点云提取出来并保存为模板，然后在不同位置进行拍摄，能够将模型信息复原出来吗？
答案肯定是可以的，借助于相机投影模型的原理，我们先了解以下几个概念：  

一、相机矩阵K

  相机标定包括两种转换，一种是从任意的世界坐标系统转换到相机坐标系统，由外在参数矩阵（Extrinsic parameter matrix）完成，另一种是从相机坐标系的3D点转换到2D图像平面坐标上，由内在参数矩阵（Instrinsic parameter matrix）完成，这一外一内的矩阵分别通过刚体运动和射影几何实现。
 

二、齐次坐标（也称为投影坐标）

1.齐次坐标定义

• 将n维坐标描述成为n+1维坐标，简单说就是在原有坐标上加一个维度。比如齐次坐标(1, 2, 1)等价于齐次坐标(2, 4, 2)…即(k, 2k, k)，k \in R，此处这些点具有尺度不变性，是齐性的，所以称为齐次坐标。

2.为什么用齐次坐标

1）仿射变换（y=Ax+b）可以通过矩阵相乘计算得出； 2）光束（相机中心线）在相机平面中可以被观察为一个点：

• 相机中心的平面在图像平面上被观察为一条线；
• 相机中心的圆锥锥点在图像平面上被观察为一个截面；

3）无限远处的点（也被称为理想点）可以用数学表示为：w=0； 4）点和线共面（ax+by+c=0）可以被优雅的描述为:

 

三、投影矩阵P

  1.如果一个3D点不是基于相机坐标系，这个点应该被转换如下图所示：
2.相机位姿可以从RT和-RTt得到：
 

四、相机参数

1.内参~相机矩阵

• 比如焦距、主点、畸变系数

2.外参~点转换

• 比如旋转和平移

有了前面的概念做基础，我们看下如何进行图像信息复原： 1.假设相机参数：焦距、主点、图像分辨率以及相机位姿已知； 2.在齐次坐标中加载构建好的点云模型； 3.相机从不同角度观察，生成图像信息：

• 得到投影矩阵：cv::Mat P = K * Rt
• 得到投影点： cv::Mat x = P * X

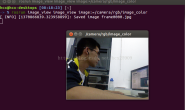
最后，我们给出部分代码及执行结果：