目录
- 一、旋转运动学
- 1.1 线速度与角速度
- 1.2 旋转坐标系下的运动学
- 二、IMU 测量模型及运动模型
- 2.1 MEMS(Micro-electromechanical Systems微电子机械系统) 加速度计工作原理
- 2.2 MEMS(Micro-electromechanical Systems微电子机械系统) 陀螺仪测量原理
- 三、IMU 误差模型
- 3.1 误差分类
- 3.2 确定性误差
- 3.2.1 六面法标定加速度 bias 和 scale factor
- 3.2.2 六面法标定陀螺仪 bias 和 scale factor
- 3.2.3 温度相关的参数标定
- 3.3 随机误差
- 3.3.1 随机误差的离散化
- 3.3.2 IMU 随机误差的标定
- 3.4 加速度计的误差模型总结
- 3.5 陀螺仪的误差模型总结
- 四、运动模型(预积分模型)离散时间处理
- 参考链接
一、旋转运动学
1.1 线速度与角速度

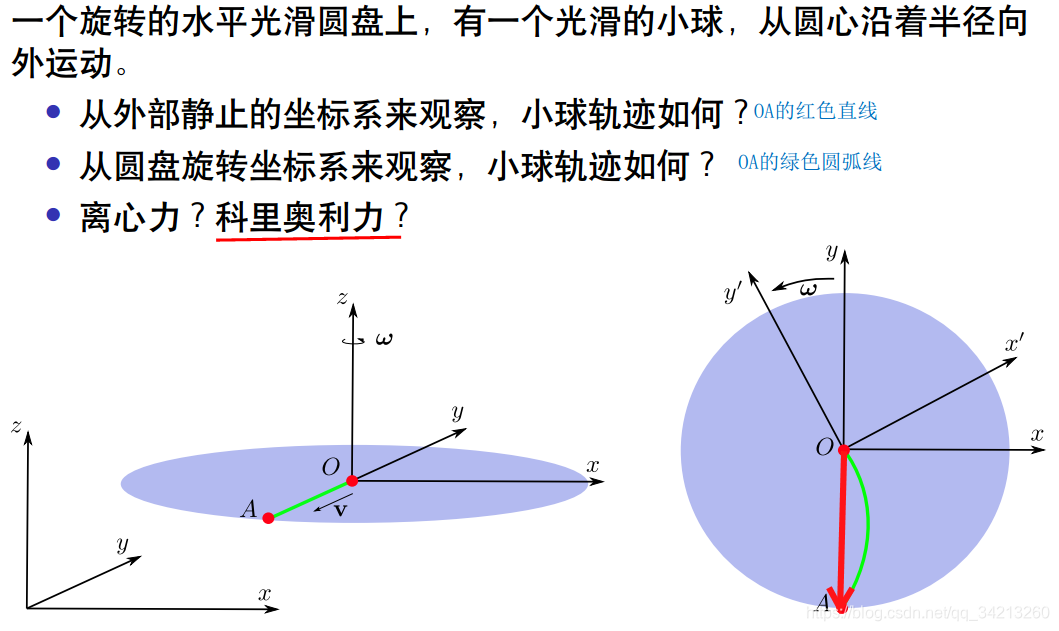
1.2 旋转坐标系下的运动学
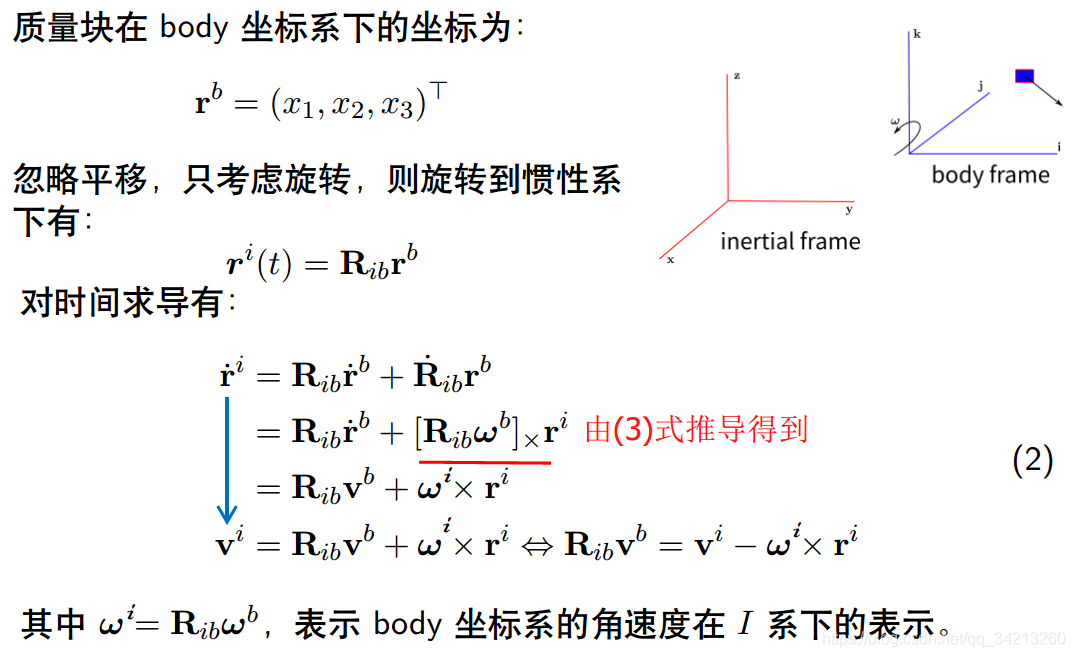 补充:右扰动模型: R[w]X=[Rw]X⋅RR[w]X=[Rw]X⋅R
补充:右扰动模型: R[w]X=[Rw]X⋅RR[w]X=[Rw]X⋅R 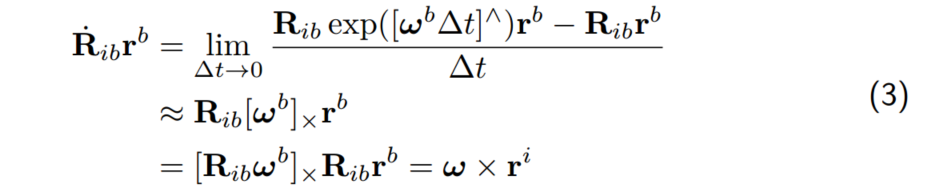

在旋转坐标系下观察,运动的物体(运动方向和旋转轴不为同一个轴时)会受到科氏力的作用。
二、IMU 测量模型及运动模型
2.1 MEMS(Micro-electromechanical Systems微电子机械系统) 加速度计工作原理

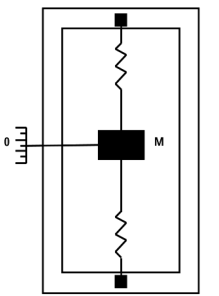
加速度变化,引起质量块位置的变化,引起电阻电容的变化。
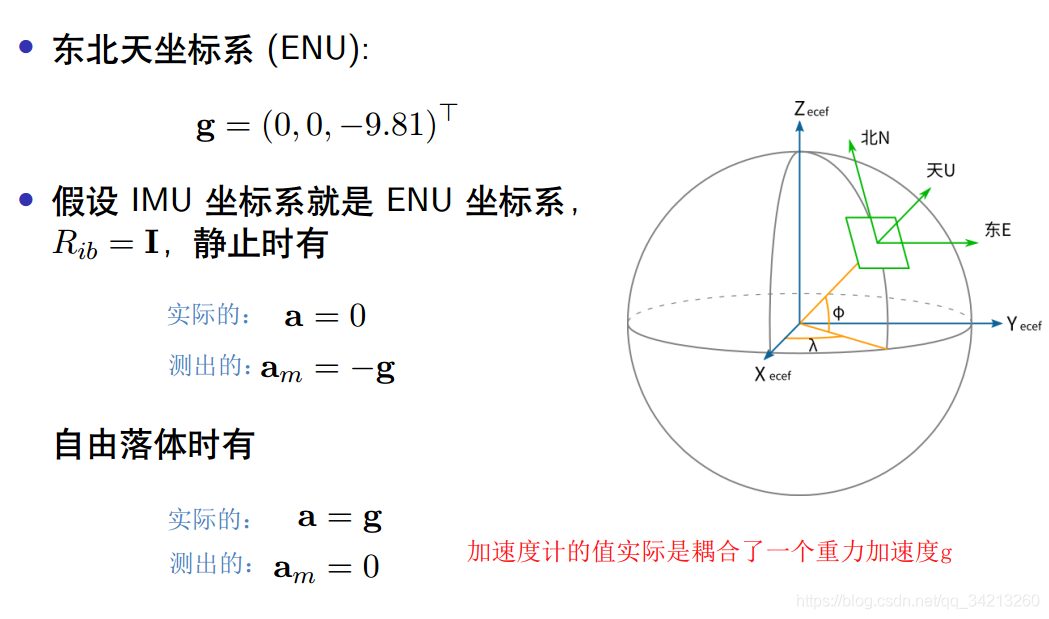
2.2 MEMS(Micro-electromechanical Systems微电子机械系统) 陀螺仪测量原理
• 陀螺仪主要用来测量物体的旋转角速度,按测量原理分有振动陀螺,光纤陀螺等。 • 低端 MEMS 陀螺上一般采用振动陀螺原理,通过测量 Coriolis force(科氏力) 来间接得到角速度。 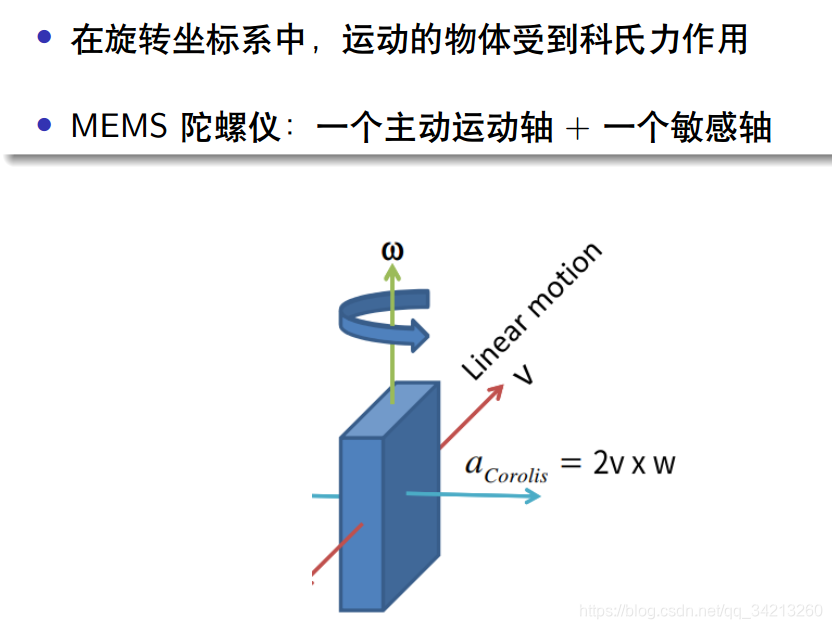
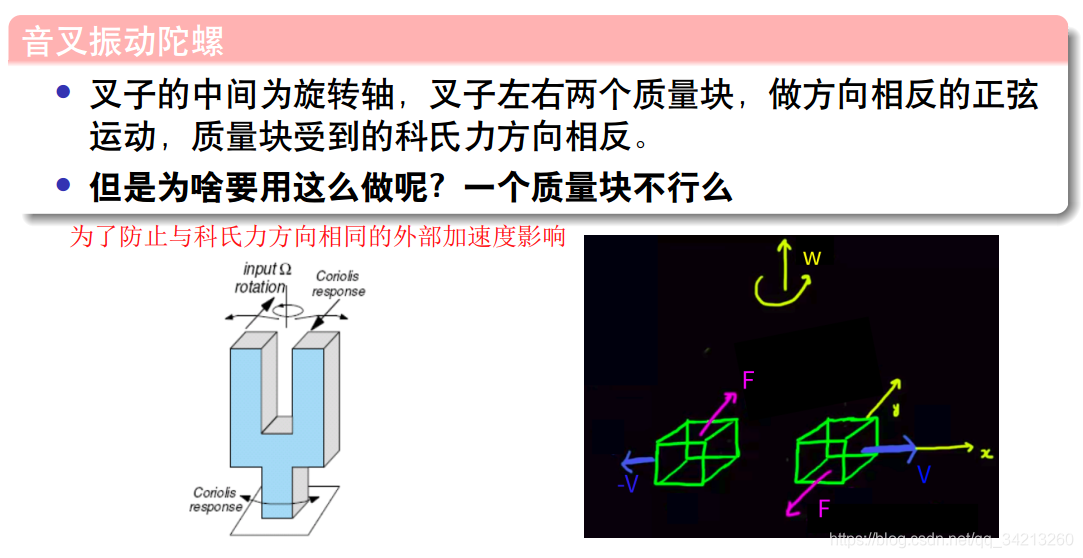

 加速度计当然也会受到科氏力影响,但是因为加速度计的质量块并不含有主动驱动的旋转运动。因此,一般情况下ω->0, 在精度要求不高的情况下,科氏力对加速度的影响可以忽略不记。
加速度计当然也会受到科氏力影响,但是因为加速度计的质量块并不含有主动驱动的旋转运动。因此,一般情况下ω->0, 在精度要求不高的情况下,科氏力对加速度的影响可以忽略不记。
三、IMU 误差模型
3.1 误差分类
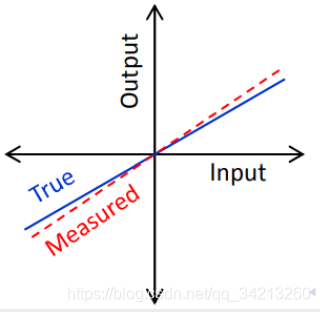
• 加速度计和陀螺仪的误差可以分为:确定性误差,随机误差。 • 确定性误差可以事先标定确定,包括: bias, scale … • 随机误差通常假设噪声服从高斯分布,确定其方差大小,包括:高斯白噪声, bias随机游走…
3.2 确定性误差



3.2.1 六面法标定加速度 bias 和 scale factor

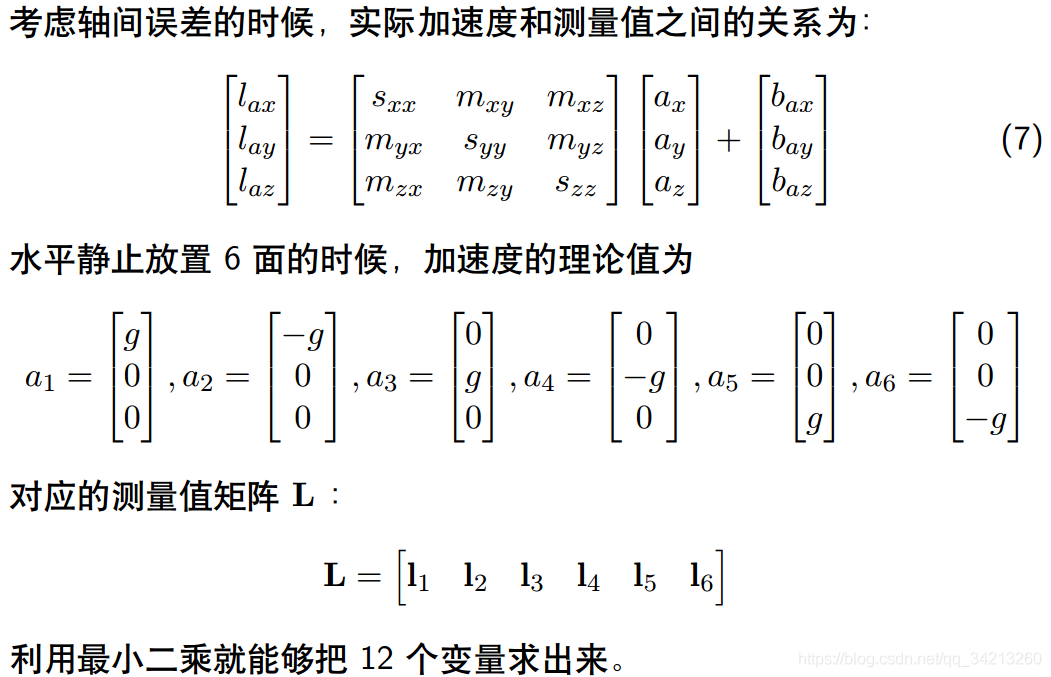
最小二乘原理可以参考我的另一篇博文: https://www.cnblogs.com/long5683/p/12073813.html
3.2.2 六面法标定陀螺仪 bias 和 scale factor
和加速度计六面法类似,只是陀螺仪的真实值由高精度转台提供,这 里的 6 面是指各个轴顺时针和逆时针旋转。
3.2.3 温度相关的参数标定

3.3 随机误差

3.3.1 随机误差的离散化
实际上, IMU 传感器获取的数据为离散采样,因此需要进行离散化 1. 高斯白噪声的离散化 

 2. bias 随机游走的离散化
2. bias 随机游走的离散化 

更详细的连续到离散的推导参见: John L Crassidis. “Sigma-point Kalman fltering for integrated GPS and inertial navigation”. In: IEEE Transactions on Aerospace and Electronic Systems 42.2 (2006), pp. 750–756.
3.3.2 IMU 随机误差的标定
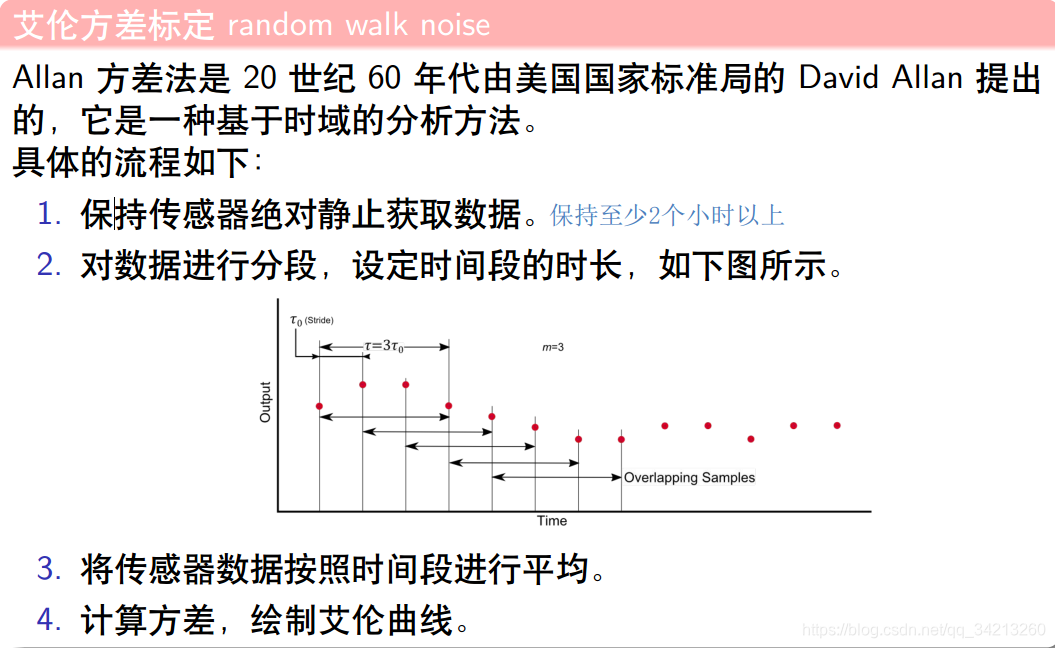
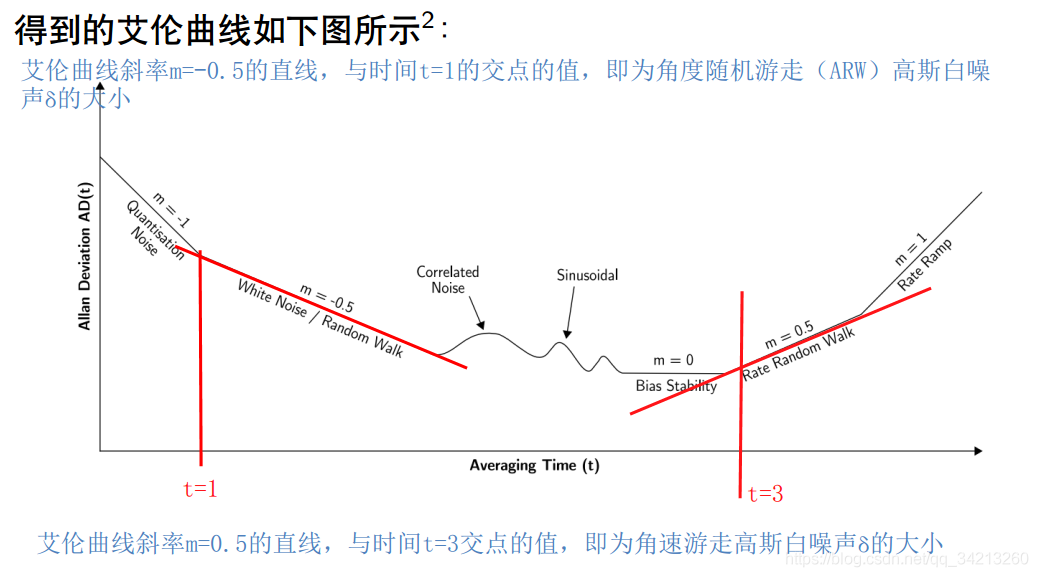
详细可参考: Allan Variance. “Noise Analysis for Gyroscopes”. In: Freescale Semiconductor Document Number: AN5087 Application Note Rev. 0 2 (2015)
3.4 加速度计的误差模型总结
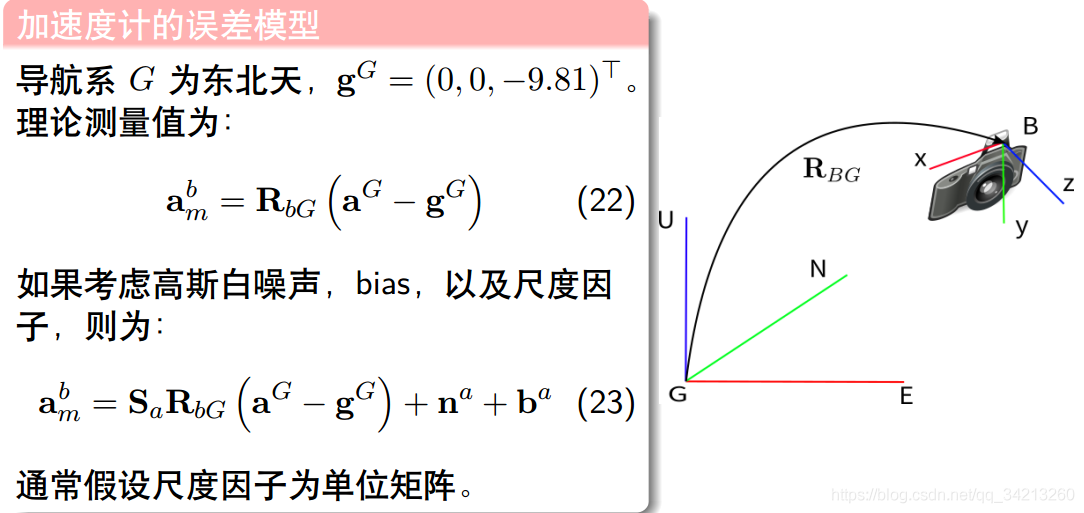
3.5 陀螺仪的误差模型总结
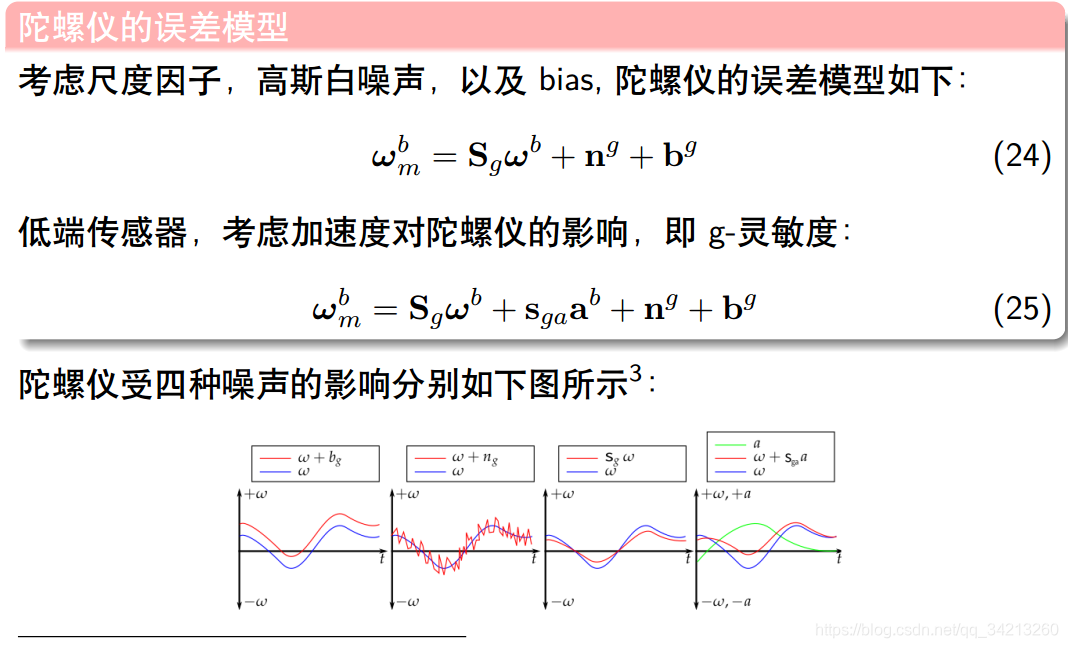
详细内容参考:MA Shelley. “Monocular visual inertial odometry on a mobile device”. In: Master’s thesis, Institut für Informatik, TUMünchen, Germany (2014)
四、运动模型(预积分模型)离散时间处理
4.1 IMU 模型

4.2 连续时间下 IMU 运动模型

4.3 运动模型的离散积分——欧拉法
 qwbt+1=qwbt+q˙wbt×Δt=qwbt⊗[10]+qwbt⊗[012ωbt]=qwbk⊗[112ωδt]qwbt+1=qwbt+q˙wbt×Δt=qwbt⊗[10]+qwbt⊗[012ωbt]=qwbk⊗[112ωδt]
qwbt+1=qwbt+q˙wbt×Δt=qwbt⊗[10]+qwbt⊗[012ωbt]=qwbk⊗[112ωδt]qwbt+1=qwbt+q˙wbt×Δt=qwbt⊗[10]+qwbt⊗[012ωbt]=qwbk⊗[112ωδt]
4.3 运动模型的离散积分——中值法

4.4 李代数表示的运动模型




 太多了就不一一放上来了,重点看文档《预积分总结与公式推导》
太多了就不一一放上来了,重点看文档《预积分总结与公式推导》
参考链接
https://www.cnblogs.com/JingeTU/p/9048986.html // 部分公式推导错误 http://paopaorobot.org/bbs/read.php?tid=181&fid=5





