英文原文链接:http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/#mathybits
注:这恐怕是全网有关卡尔曼滤波最简单易懂的解释,如果你认真的读完本文,你将对卡尔曼滤波有一个更加清晰的认识,并且可以手推卡尔曼滤波。原文作者使用了漂亮的图片和颜色来阐明它的原理(读起来并不会因公式多而感到枯燥),所以请勇敢地读下去!
目录
1. 背景
1.1 滤波与滤波器(Filter)
1.2 卡尔曼滤波算法
1.3 问题描述
2. 状态估计
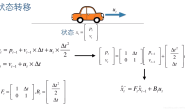
2.1 问题的矩阵形式表示
2.2 External influence
2.3 External uncertainty
3. 状态更新
3.1 利用测量进一步修整状态
3.2 公式推导
3.3公式汇总
4. 总结
5. 参考文献
1. 背景
1.1 滤波与滤波器(Filter)
首先援引来自知乎大神的解释。
“一位专业课的教授给我们上课的时候,曾谈到:filtering is weighting(滤波即加权)。滤波的作用就是给不同的信号分量不同的权重。最简单的loss pass filter, 就是直接把低频的信号给1权重,而给高频部分0权重。对于更复杂的滤波,比如维纳滤波, 则要根据信号的统计知识来设计权重。
从统计信号处理的角度,降噪可以看成滤波的一种。降噪的目的在于突出信号本身而抑制噪声影响。从这个角度,降噪就是给信号一个高的权重而给噪声一个低的权重。维纳滤波就是一个典型的降噪滤波器。”
1.2 卡尔曼滤波算法
Kalman Filter 算法,是一种递推预测滤波算法,算法中涉及到滤波,也涉及到对下一时刻数据的预测。
Kalman Filter 由一系列递归数学公式描述。它提供了一种高效可计算的方法来估计过程的状态,并使估计均方误差最小。卡尔曼滤波器应用广泛且功能强大:它可以估计信号的过去和当前状态,甚至能估计将来的状态,即使并不知道模型的确切性质。
Kalman Filter 也可以被认为是一种数据融合算法(Data fusion algorithm),已有50多年的历史,是当今使用最重要和最常见的数据融合算法之一。Kalman Filter 的巨大成功归功于其小的计算需求,优雅的递归属性以及作为具有高斯误差统计的一维线性系统的最优估计器的状态。
Kalman Filter 只能减小均值为0的测量噪声带来的影响。只要噪声期望为0,那么不管方差多大,只要迭代次数足够多,那效果都很好。反之,噪声期望不为0,那么估计值就还是与实际值有偏差[3]。
1.3 问题描述
我们会有一个疑问:卡尔曼滤波到底是如何解决实际问题的呢?

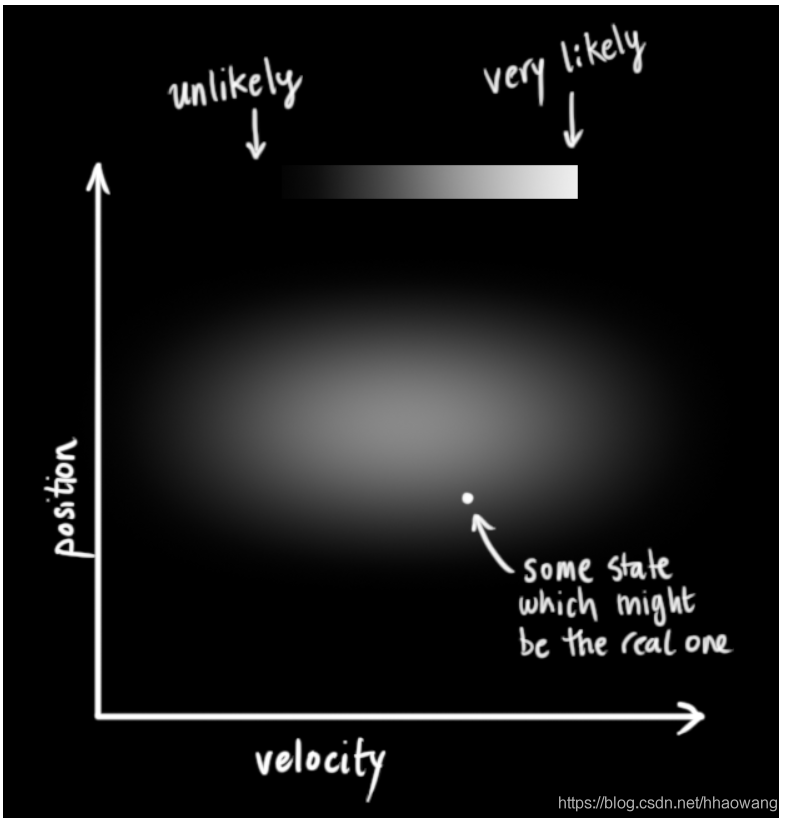
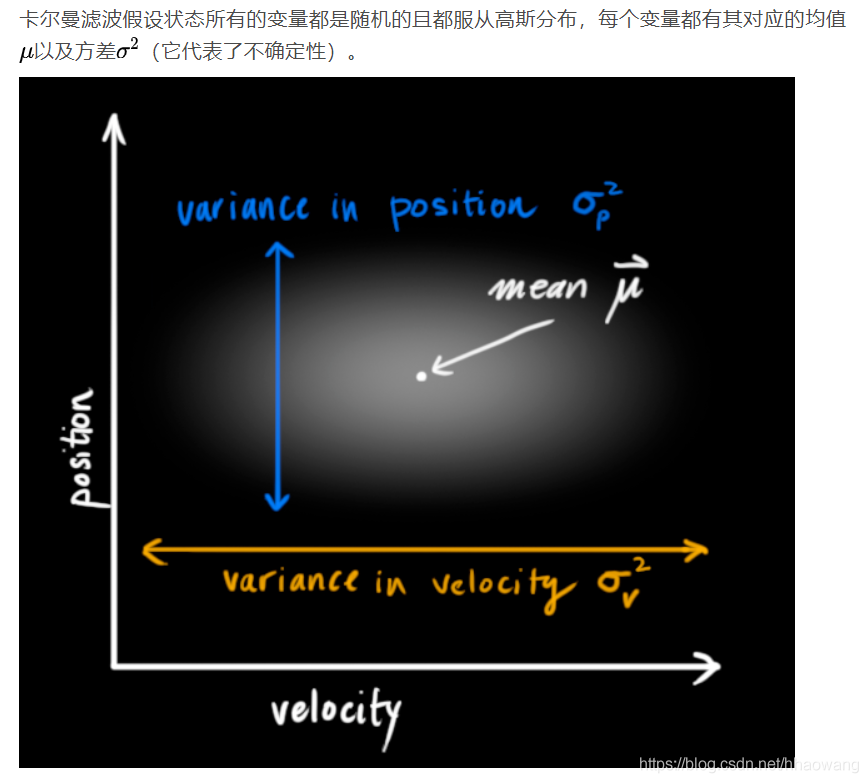
在上图中,位置和速度是不相关(uncorrelated)的,这意味着某个变量的状态不会告诉你其他变量的状态是怎样的。
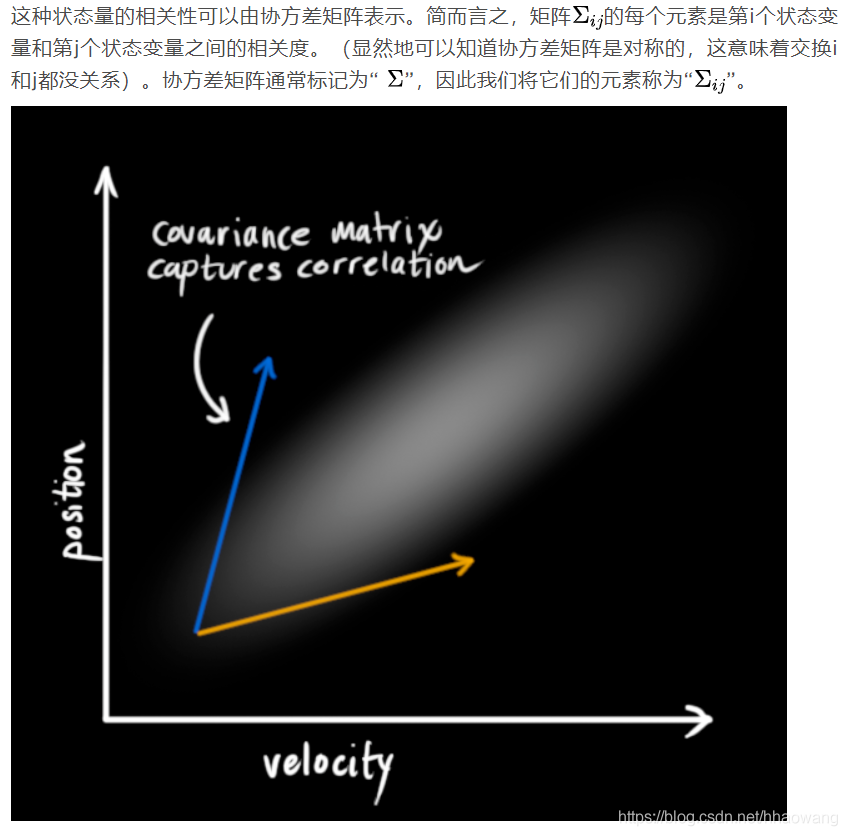
即,我们虽然知道现在的速度,但无法从现在的速度推测出现在的位置。但实际上并非如此,我们知道速度和位置是有关系的(correlated),这样一来二者之间的组合关系变成了如下图所示的情况。
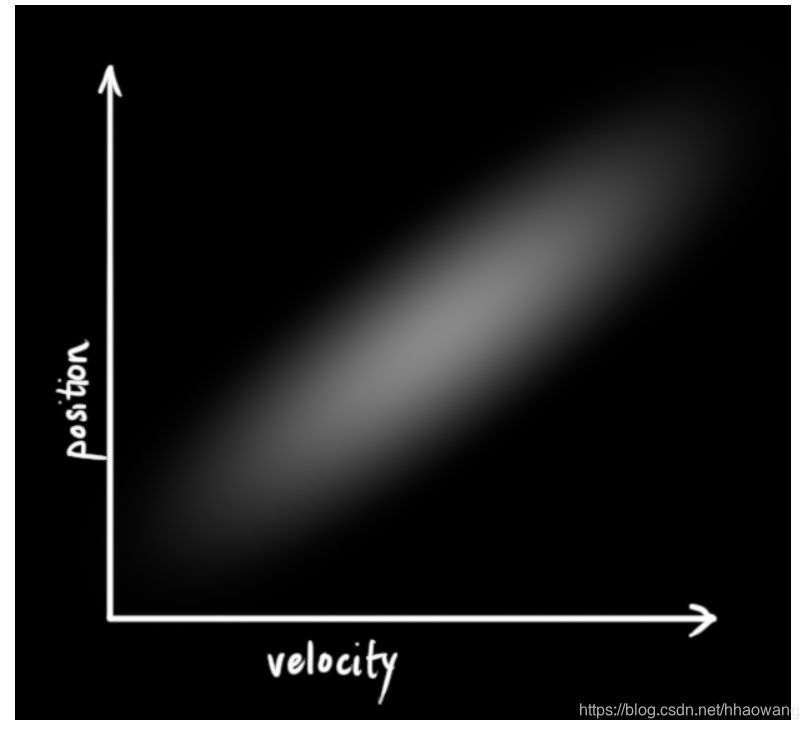
这种情况是很容易发生的,例如,如果速度很快,我们可能会走得更远,所以我们的位置会更大。如果我们走得很慢,我们就不会走得太远。
这种状态变量之间的关系很重要,因为它可以为我们提供更多信息:One measurement tells us something about what the others could be。这就是卡尔曼滤波器的目标,我们希望从不确定的测量中尽可能多地获取信息!
2. 状态估计
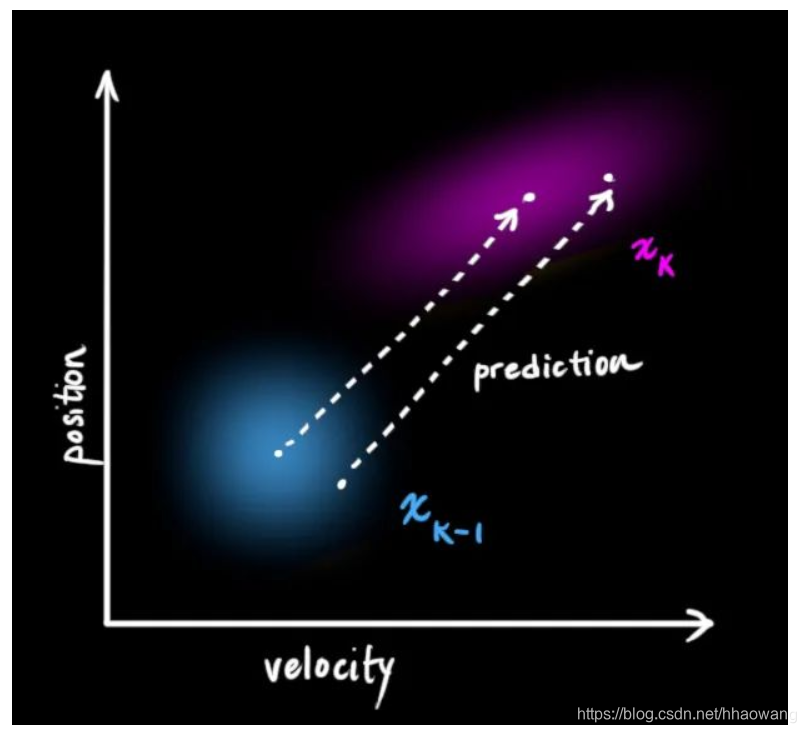
2.1 问题的矩阵形式表示


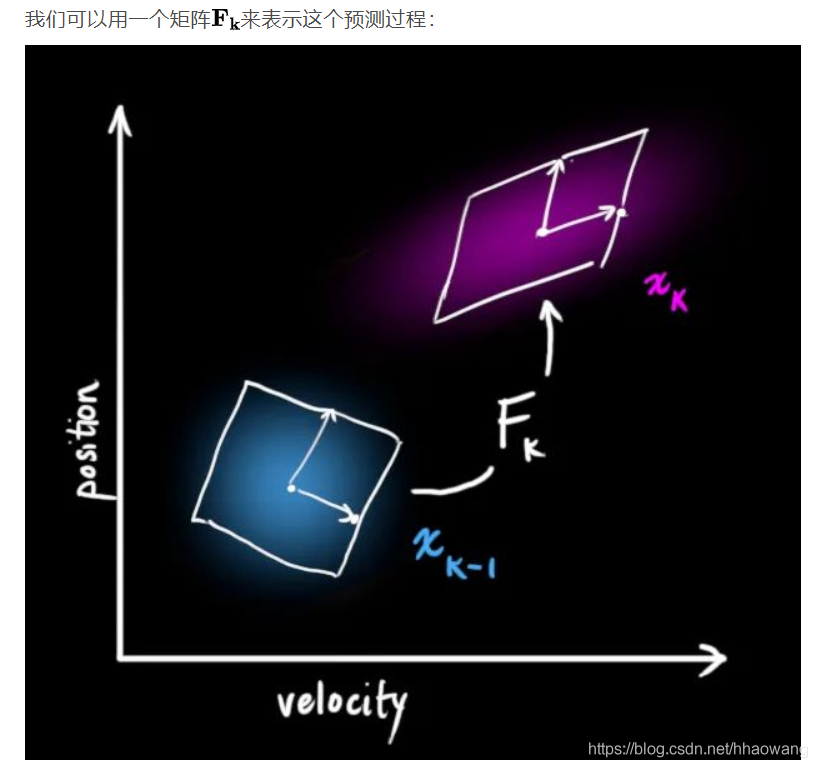


2.2 External influence

如果我们的预测并不是100%准确模型,这会发生什么呢?
2.3 External uncertainty
如果状态仅仅依赖其自身的属性进行演进,那一切都会很好。如果状态受到外部因素进行演进,我们只要知道这些外部因素是什么,那么一切仍然很好。
但在实际使用中,我们有时不知道的这些外部因素到底是如何被建模的。例如,我们要跟踪四轴飞行器,它可能会随风摇晃;如果我们跟踪的是轮式机器人,则车轮可能会打滑,或者因地面颠簸导致其减速。我们无法跟踪这些外部因素,如果发生任何这些情况,我们的预测可能会出错,因为我们并没有考虑这些因素。
通过在每个预测步骤之后添加一些新的不确定性,我们可以对与“世界”相关的不确定性进行建模(如我们无法跟踪的事物):
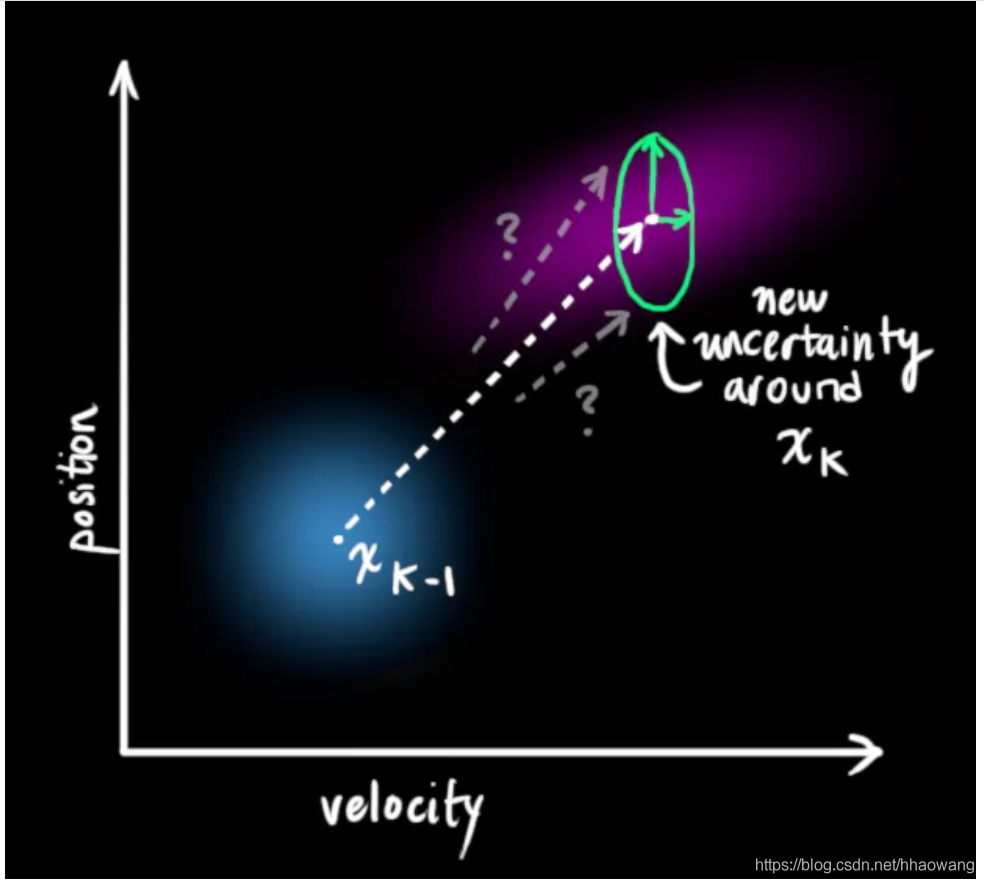

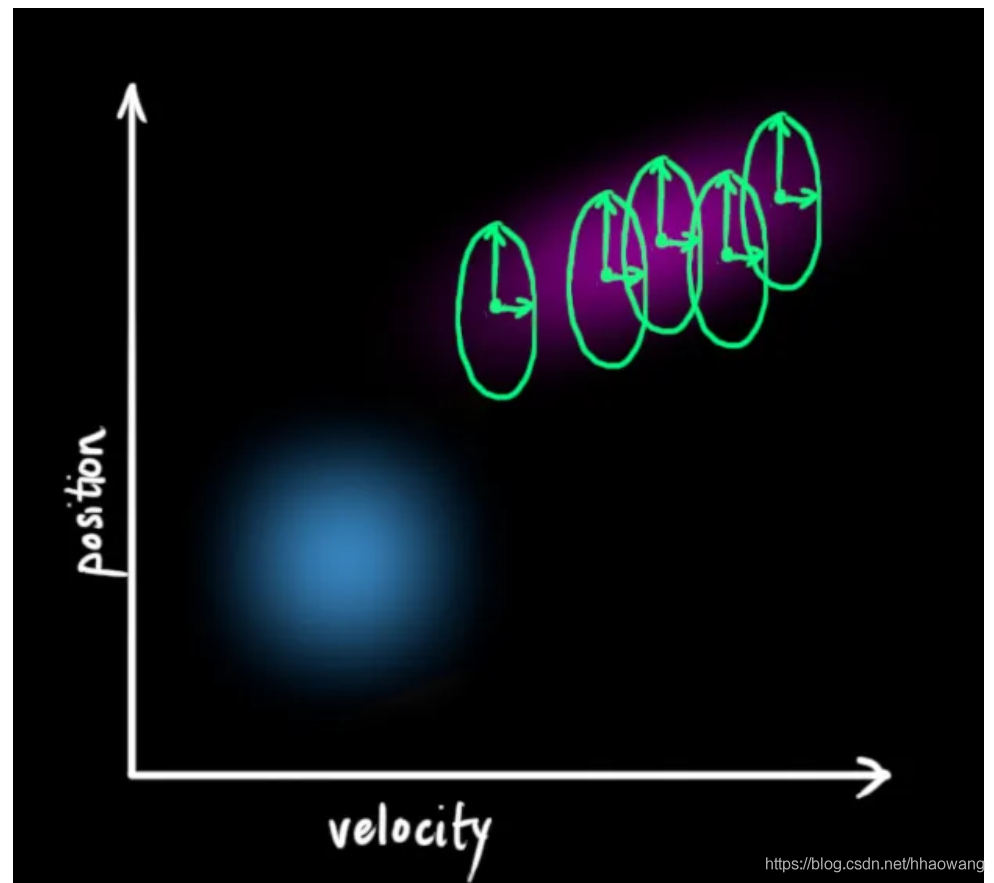
这将产生一个新的高斯分布,其协方差不同(但均值相同):
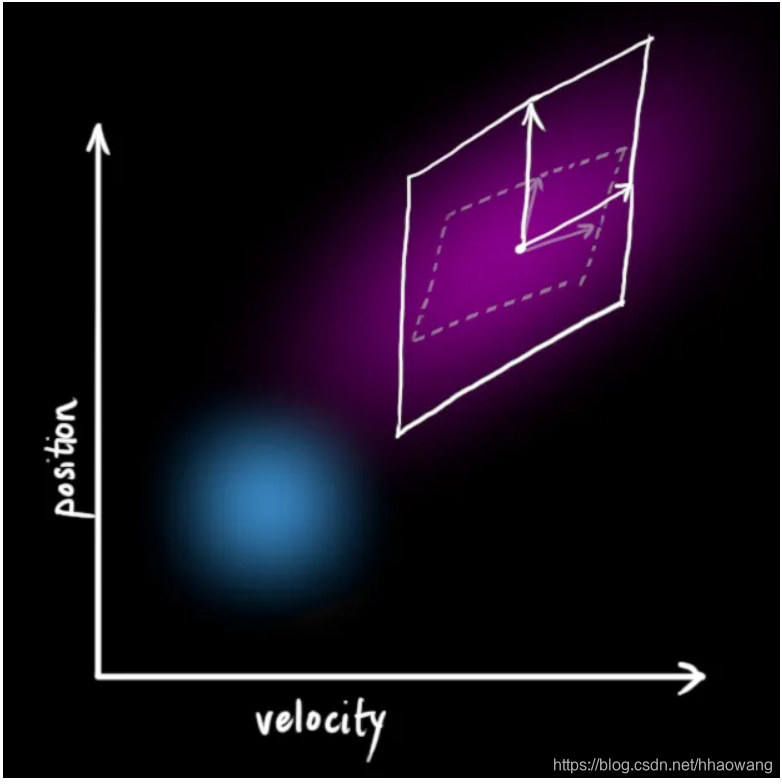

3. 状态更新
3.1 利用测量进一步修整状态
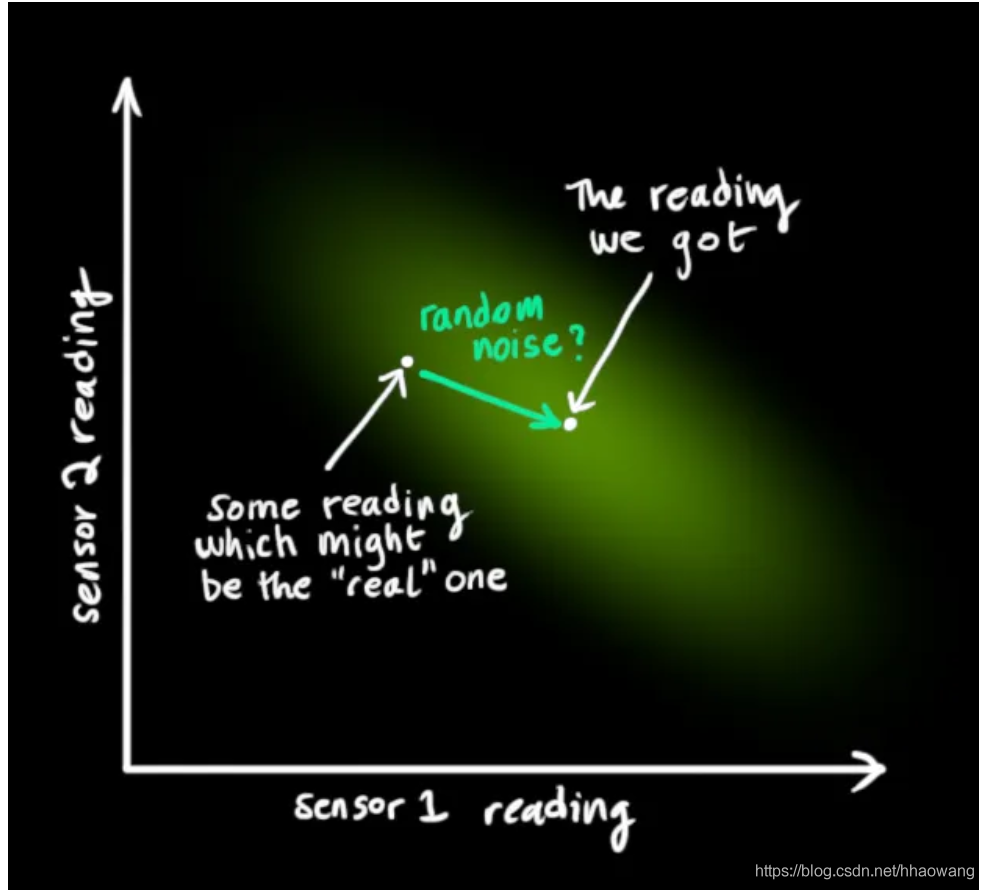
假设我们有几个传感器,这些传感器可以向我们提供有关系统状态的信息。就目前而言,测量什么量都无关紧要,也许一个读取位置,另一个读取速度。每个传感器都告诉我们有关状态的一些间接信息(换句话说,传感器在状态下运作并产生一组测量读数)。
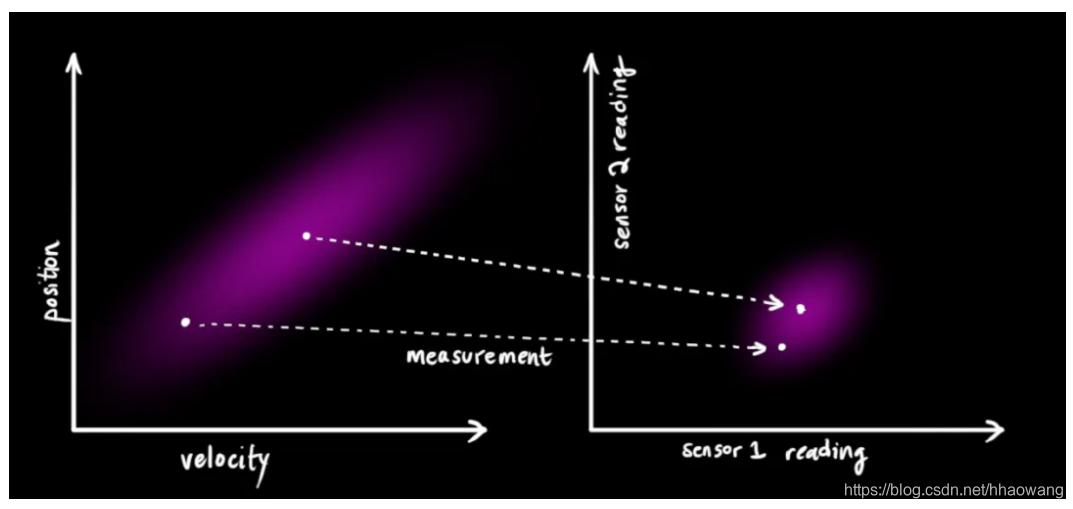
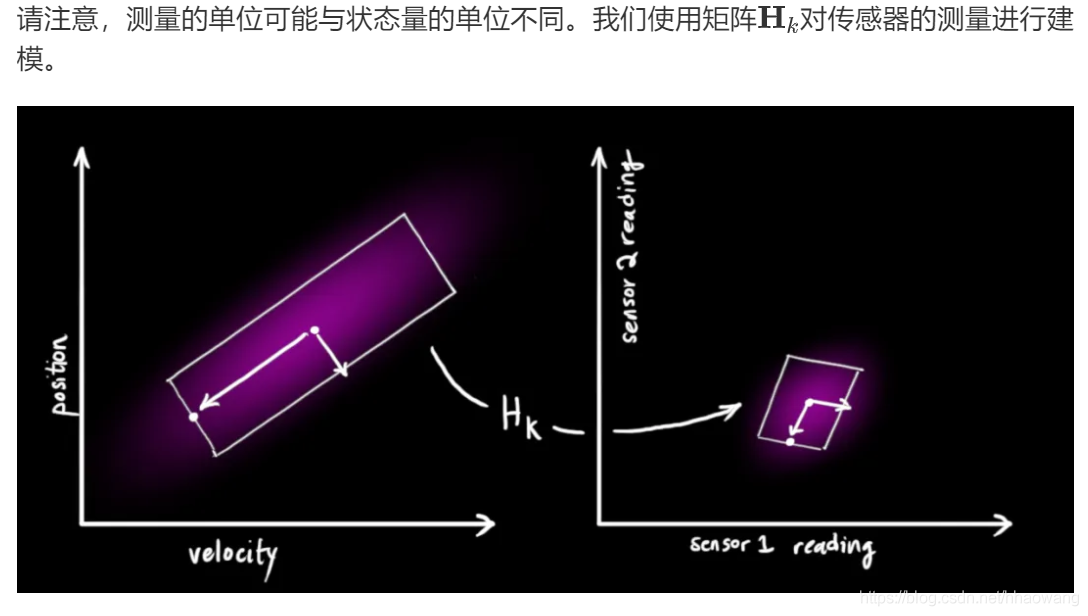

卡尔曼滤波器的伟大之处就在于它能够处理传感器噪声。换句话说,传感器本身的测量是不准确的,且原始估计中的每个状态都可能导致一定范围的传感器读数,而卡尔曼滤波能够在这些不确定性存在的情况下找到最优的状态。

根据传感器的读数,我们会猜测系统正处于某个特定状态。
但是由于不确定性的存在,某些状态比其他状态更可能产生我们看到的读数:

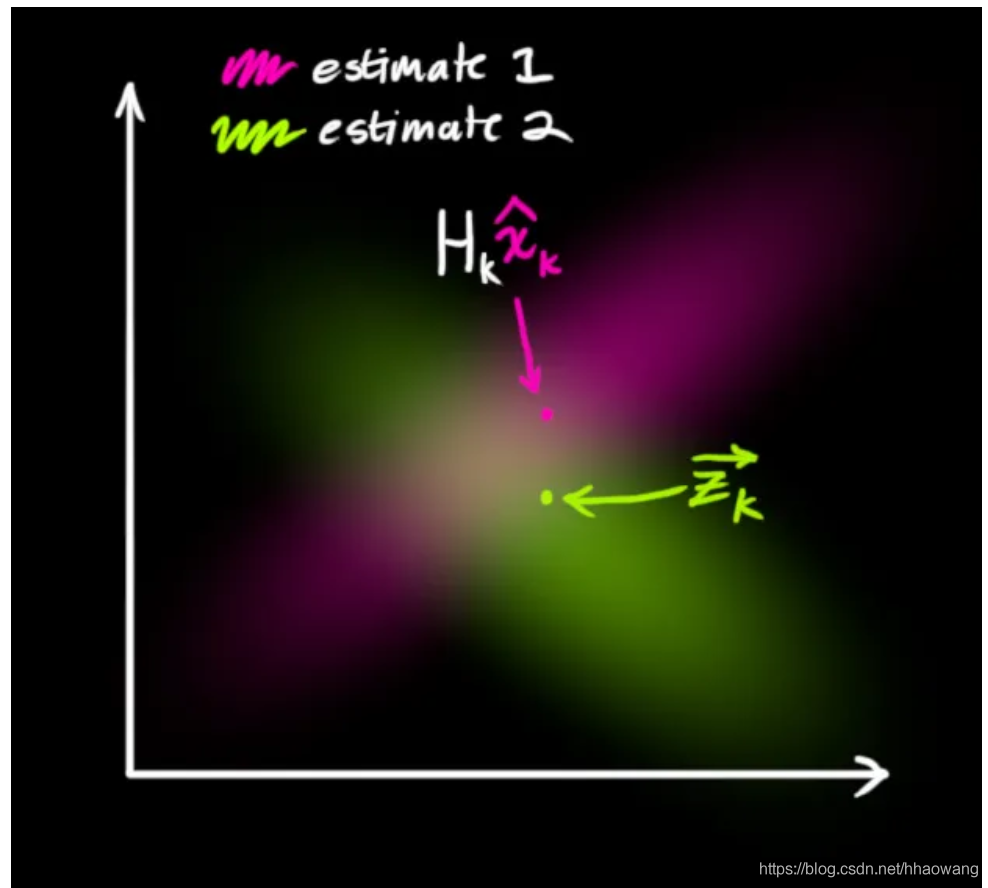

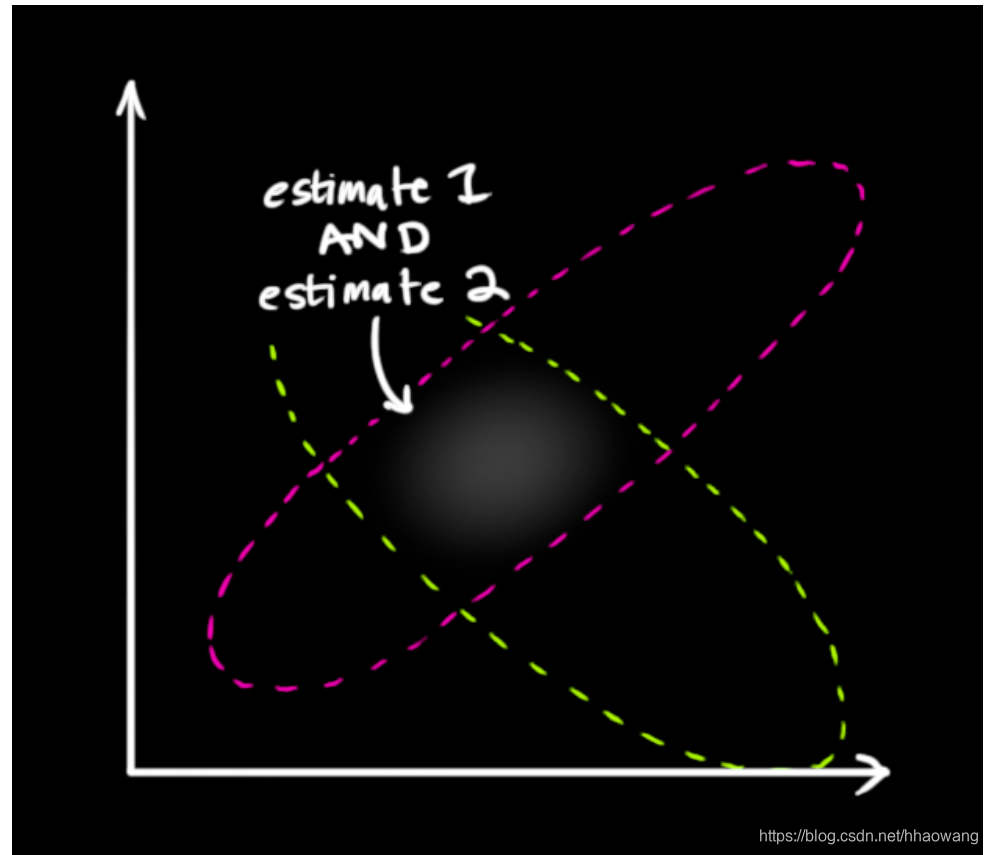
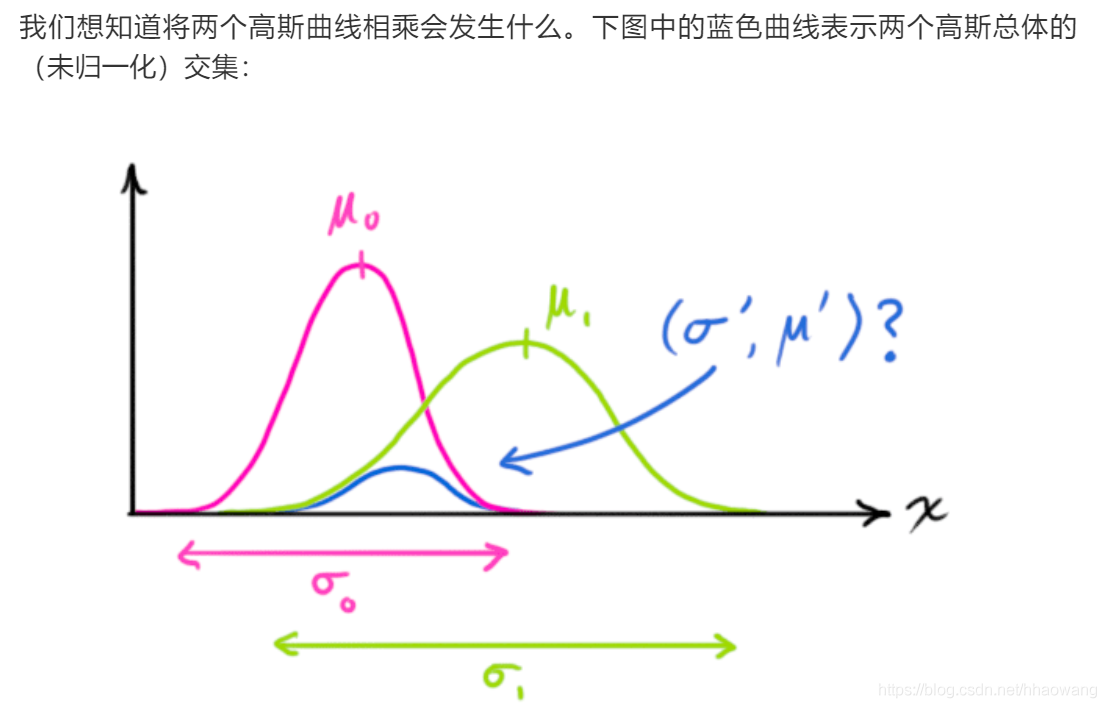
两个概率分布相乘得到的就是上图中的重叠部分。而且重叠部分的概率分布会比我们之前的任何一个估计值/读数都精确得多,这个分布的均值就是两种估计最有可能配置(得到的状态)。
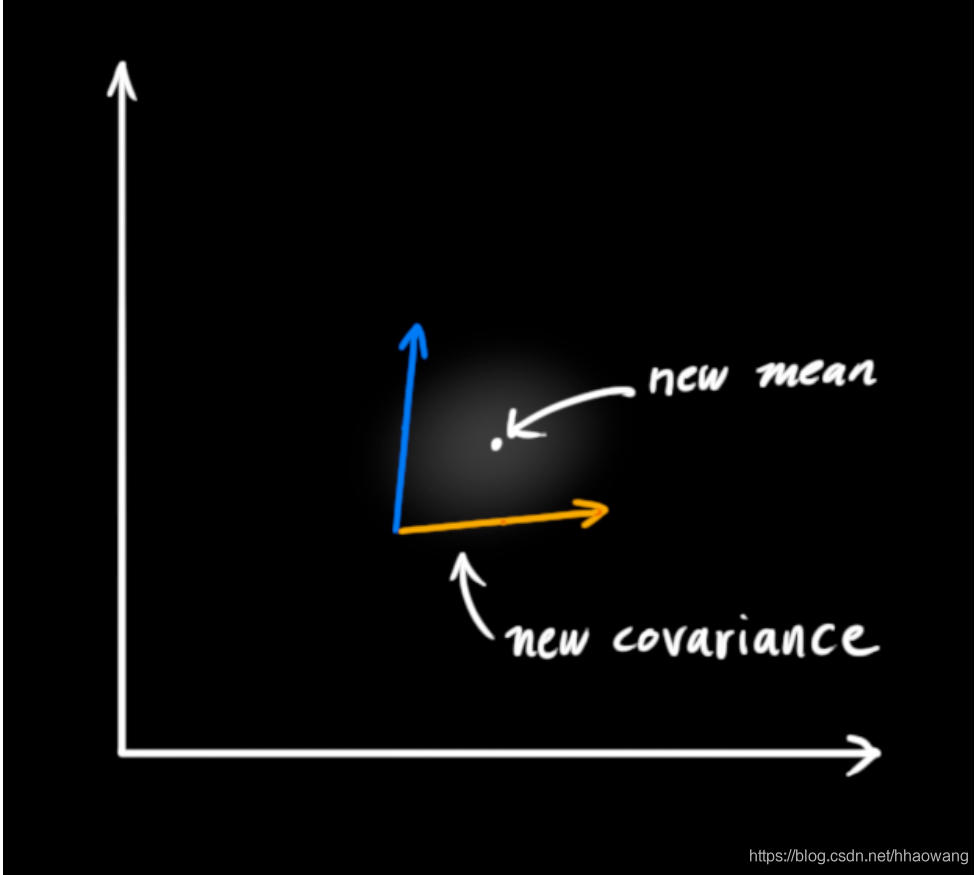
事实证明,两个独立的高斯分布相乘之后会得到一个新的具有其均值和协方差矩阵的高斯分布!下面开始推公式。
3.2 公式推导



3.3公式汇总
预测阶段:Prediction Step

更新阶段:Update Step

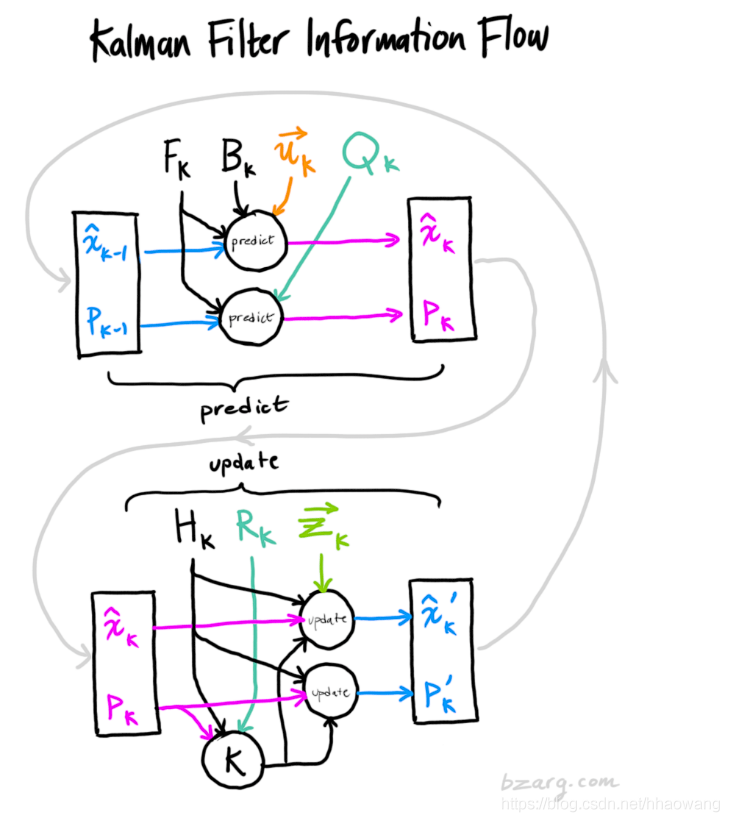
4. 总结


5. 参考文献
[1]: How a Kalman filter works, in pictures, 图解卡尔曼滤波是如何工作的:
http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/#mathybits
[2]: A geometric interpretation of the covariance matrix, 协方差矩阵的几何解释:
https://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix
[3]: Kalman Filter 卡尔曼滤波:
https://sikasjc.github.io/2018/05/08/kalman_filter