引言
这部分可以说是独立于我们整个项目的一小节，不过也是极为重要的一小节，这一节的学习可以帮助我们去了解神经网络。我们用一个很简单的例子进行参考，本节内容的知识参考了莫烦python的系列教程。 https://space.bilibili.com/243821484?spm_id_from=333.788.b_765f7570696e666f.1 好了，话不多说，我们进入学习。
正文
我们直接开始代码的编写 这个是单独的项目，所以大家可以跟着一步一步来完成并实现这个代码。 首先我们包含一下可能会用到的头文件
import torch
from torch.autograd import Variable
import torch.nn.functional as F
# 导入plot模块需要以下三句
import matplotlib.pyplot as plt
import matplotlib; matplotlib.use('TkAgg')
import os;os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
因为我用的pycharm，当时写代码的时候因为plot没法弹窗，后来查完发现按上述方法写就可以了。
我们继续正题，我们下面来造一组伪随机点，代码如下
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
y = x.pow(2) + 0.2 * torch.rand(x.size())
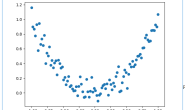
因为在torch中，数据是有维度的，因此要用unsqueeze来把一维的数据变成二维的。 这串数据其实就是函数y = x^2（这边表示x的平方）上离散的点加上噪声的效果。 而我们的目的呢，就是依靠神经网络来拟合曲线。 大家可以用下面这两行代码把这堆离散点显示出来
plt.scatter(x.data.numpy(),y.data.numpy())
plt.show()
效果如上图。就是在y = x^2的基础上增加了一些噪点。 接下来我们开始搭建一个简单的神经网络。 代码如下：
class Net(torch.nn.Module):
def __init__(self, n_features, n_hidden, n_output):
super().__init__()
self.hidden = torch.nn.Linear(n_features, n_hidden) # 隐藏层
self.predict = torch.nn.Linear(n_hidden, n_output)
def forward(self, x):
x = F.relu(self.hidden(x))
x = self.predict(x)
return x
我们用了一个class来定义我们的net，这个class必须要继承torch.nn.Module这个模块，这是net的一个主模块，很多功能都包含在这个模块中。 其中的init构造方法和forward前向传递函数是比较重要的。 init构造方法中的super().init()继承父类是必要操作，下面就是我们自己定义的层了。我们的层信息都是这个模块中的一个属性，也就是我们的一层神经网络。首先是hidden隐藏层，其所包含的东西是我们的神经网络有多少个输入和多少个输出。 所以我们把参数传入，也就是输入数据的个数。 第二个层就是预测的神经网络层，我们预测的层接收的神经元就是隐藏层输出的神经元。预测层因为我们只是预测y的值，因此输出值就是1。 接下来就是完成forward前向传递函数。 我们需要使用一个激励函数来激活一下传入的数据也就是relu这个函数。然后再把得到的x传入predict得到我们的输出。
这样我们就搭完了一个比较简单的神经网络，这个神经网络有n_features个输入，n_output个输出，以及n_hidden个隐藏层，下面我们进行实例化。 代码如下
net = Net(1, 10, 1)
参数分别是1个输入x，10个隐藏层，1个输出值y。 我们可以用print(net)来打印出我们神经网络结构。大家可以自己尝试，这里就不做试验了，我们继续往下进行
接下来我们需要优化我们的神经网络，这回用到optim模块里的函数，我们用最一般的SGD优化器来优化网络。 代码如下
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)
第一个参数是把神经网络的全部参数传入SGD，第二个lr就是学习效率，这个越高，学习的越快，不过快未必好，因为学习的快会忽略掉很多特征点，因此需要取一个比较合适的值，这里我们就先设置成0.2，一般都是小于1的数。
下面我们来定义计算误差的手段，我们用到的是MSELoss也就是均方差函数，代码如下
loss_func = torch.nn.MSELoss()
OK，这一步结束之后，我们就要开始训练了，训练的代码如下
for t in range(500):
prediction = net.forward(x)
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if t&5==0:
plt.cla()
plt.scatter(x.data.numpy(),y.data.numpy())
plt.plot(x.data.numpy(),prediction.data.numpy(),'r-',lw=5)
print('LOSS:',float(loss.data))
plt.pause(0.1)
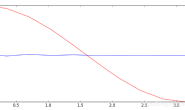
我们训练500步，也就是循环的次数，然后传入我们的x并计算损失，也就是预测值和真实值的误差。 然后进入优化，先将梯度设0，接着反向传递，然后优化梯度。这就是整个的训练过程。 然后我们把训练的过程进行可视化，我们设置每学习五步，打印一次信息。 接下来开始运行， 效果如下：
经过学习次数的不断迭代，我们可以很清晰的看到曲线从一条水平线不断拟合到y=x^2的函数上，LOSS也在迭代中不断减小。 这就是一个简单的神经网络的搭建例子，可以帮助大家更好的理解和掌握神经网络。 这个小项目的全部代码我粘贴在下面，图方便的同学可以直接复制这个代码运行查看效果。
import torch
from torch.autograd import Variable
import torch.nn.functional as F
# 导入plot模块需要以下三句
import matplotlib.pyplot as plt
import matplotlib; matplotlib.use('TkAgg')
import os;os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
y = x.pow(2) + 0.2 * torch.rand(x.size())
class Net(torch.nn.Module):
def __init__(self, n_features, n_hidden, n_output):
super().__init__()
self.hidden = torch.nn.Linear(n_features, n_hidden) # 隐藏层
self.predict = torch.nn.Linear(n_hidden, n_output)
def forward(self, x):
x = F.relu(self.hidden(x))
x = self.predict(x)
return x
net = Net(1, 10, 1)
plt.ion()
plt.show()
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)
loss_func = torch.nn.MSELoss()
print(net.parameters())
for t in range(500):
prediction = net.forward(x)
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if t&5==0:
plt.cla()
plt.scatter(x.data.numpy(),y.data.numpy())
plt.plot(x.data.numpy(),prediction.data.numpy(),'r-',lw=5)
print('LOSS:',float(loss.data))
plt.pause(0.1)
plt.ioff()
plt.show()
总结
本章节在我们继续项目的神经网络搭建之前，带大家尝试了一个简单的神经网络搭建的例子，这个可以帮助大家更好的对神经网络进行理解，当然这个例子也是在我学习神经网络的过程中看到的比较简单并且效果非常直观的一个例子了，大家可以在本节开头我提到的莫烦python的个人主页找到他对pytorch更为细致的教程讲解。
OK，那么本章就结束了，从下一章节开始我们回到我们车牌字符识别的项目中，我们将会在下一个章节中进行我们用于车牌识别的CNN卷积神经网络的搭建，这个将会比我们本节搭建的网络稍复杂一些。
