引言

在真实需求中，当我们的机械臂已经拿到了一支笔，那怎么设定轨迹让它画一只鸭子之类的呢，或者怎么样让机械臂拿到杯子后挂在墙上呢？我们需要知道手臂状态（位置状态、速度状态）和时间的关系，从而拟合出一条连续（重点）的曲线供机械臂达到目的。这就属于“轨迹规划”内容了。

轨迹规划

Joint space、Actuator space、Cartesian space的区别

Joint space下的轨迹规划

Cartesian space下的轨迹规划

Joint 、Cartesian space下轨迹规划的优缺点

如何拟合曲线 (重点)

三次多项式（Cubic Polynomials）（基础）

未知中间点速度情况下的求解

(1)“手动”定义中间点求解

(2)电脑自动生成中间点（推荐）

轨迹规划

说白了就是给你两个位置点，起始点和终点，你自己定义中间点（via point），把起始点和终点用平滑曲线连起来就行。其实就是拟合曲线嘛……… 我理解的轨迹规划的核心目的在于得到关节的驱动数值的连续平滑曲线，也就是说主要是求解曲线的未知参数。如果没有关节的驱动，你怎么到达目标位置？轨迹：机械手臂末端点或参做点的位置、速度、加速度对时间的历程。轨迹规划的好处：轨迹规划后，可以使用不同形态类型的机械臂使用相同轨迹。理想轨迹是物体运动的位置连续，速度也是连续的。我们都知道，假如速度不连续，忽大忽小，这就要求它的加速度突然变大，这会给机械臂关节造成力的负担，很大可能出现误差，因此我们的轨迹规划最好是连续的。在轨迹规划下，还分两种类型的规划：Joint space、Certesian space下的轨迹规划，在这先解释下。

Joint space、Actuator space、Cartesian space的区别

[前提假设] 我们的机械臂是六个自由度的，六个关节都是转轴驱动的。也假设我们已经定义好了起始、中间、终点的位置信息和姿态信息。
$\large D$ 代表了我们的手末端的位置，
$\large \Theta$ 代表了手末端的姿态，这两个是我们的需求点。

Joint space下的轨迹规划

机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动 1）知道位置，就能通过逆向运动学（IK），反向求解出有六个自由度的机械臂它六个转轴需要的角度。 2）拟合曲线，就是轨迹规划啦，得到这些点连续平滑的函数表示（多种）。就是找函数关系（横纵轴的映射）。 3）再借由顺向运动学（FK）验证这个函数能否经过我们在（1）定义好的点，使得机械臂通过我们规定的点，达到我们想要的位置，以此测试函数是否正确。 4）检验可行性，比如这个轨迹是不是可能会撞到现实空间中的某些东西之类的。

Cartesian space下的轨迹规划

机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动 1）拟合曲线，直接做轨迹规划，找出他们的函数式。 2）逆向求解出达到这个位置需要机械臂的每个转轴转动的度数，检验求解出的角度是否超出了机械臂转动角度的最大范围等。 3）检验可行性，检测该轨迹在现实中是否会碰到障碍物。

Joint 、Cartesian space下轨迹规划的优缺点

一般都是用Cartesian space做规划，因为这个更直接地符合我们的需求，直接根据需求得到轨迹就行了啊，步骤少。然而它有一个缺点是它计算量相对于Joint space大得多，因为我们是先对手臂需要的姿态
$\large \Theta$ 位置
$\large D$ 拟合它的曲线（从几个点变成了无数个点），然后才去计算驱动关节需要的角度——反推出好多好多个姿态位置下与之一一对应的所有驱动角度，这十分考核机械臂的算力，尤其对于实时的机械臂。而Joint space就不同了，我们先计算姿态
$\large \Theta$ 位置
$\large D$ 需要的关节驱动角度数值，然后再拟合这些角度数值的曲线，拟合曲线的计算比反推无数个姿态位置对应的无数个角度要简单得多。我前面说了，我个人理解的轨迹规划的核心求解目的是——得到关节驱动的拟合曲线。如果使用Joint space的话，在第二步就能得到这个曲线，之后的3、4步都是验证而已。那为什么大家很少用计算量更少的Joint space呢？因为Cartesian更直观，他直接规划出位置的轨迹，而Joint规划的是关节角度的变换轨迹，不直观。然而我还是不太理解为啥很少人用 joint….难道是因为它步骤多么？

如何拟合曲线

拟合曲线的方法很多，可以使用机器学习的监督算法，当然小规模地轨迹也可以直接使用excel /逃。我们在轨迹规划中一般使用三次多项式，一整个曲线中往往是多段参数不同的多项式曲线组合起来的。
机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动我们首先了解单段三次多项式（红色框内），再了解多段中的求解。

三次多项式（Cubic Polynomials）（基础）

已知两侧的点坐标(假设某时刻下的角度、速度已知),用三次多项式求角度
$\large \theta$ 和时间
$\large t$ 的关系式，即需要求出
$\large a_{0....4}$ ：
机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动 一般解法： 未知的
$\large a_{0....4}$ 很容易如下求解出来：
其中[
$\large \Theta$ ]是角度，
[
$\large \Theta$ 点]代表角速度，[
$\large \Theta$ 点点]代表角加速度。
机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动 矩阵表达 如果用矩阵来表示上述运算，则是：
(注：此T矩阵与前几章的信息矩阵不同)
$\large \Theta _{i}$ 代表起点
$\large i$ 的位置，
$\large \Theta _{i+1}$ 代表终点
$\large i+1$ 的位置，
$\large \Theta _{i}$ 点代表起点i的速度，
$\large \Theta _{i+1}$ 点代表终点
$\large i+1$ 的速度。由于T矩阵满足性质有逆矩阵，所以该式可以变化为：
机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动这个是单个三次多项式的求解。

未知中间点速度情况下的求解

在上面的三项多项式中，我们是假设我们已知两侧的角度和速度才能求解多项式，在实际轨迹规划中，我们只知道头尾点的位置、速度条件，我们并不知道中间点(via point)的位置和速度，那如何定义它呢？有好多种方法：根据特殊的需求直接定义（不推荐）、让电脑自己算出适合的速度（例如多段三次多项式）、广义多项式等等方法。

(1)“手动”定义中间点求解

机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动这些方式都是定死规则，一开始就定义好了中间点是哪个，所以就能很容易得到速度值，然后利用三次多项式（Cubic Polynomials）（基础）中最后得到的矩阵求解即可。

(2)电脑自动生成中间点（推荐）

多段三次多项式

使用多段三次多项式的好处是，中间点不用自己定义，它是电脑自己算出来的，而且比手动定义的更有连续性。上面手动定义中间点的图也有个“自动定义”，但是那个是在“人定的死规则”下让电脑生成的我们能知道的中间点，并不是电脑自动算出来的连我们都不知道的中间点。 直接举例
机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动 [假设条件] 中间点是
$\large \Theta_{1}$ ,并且已知
$\large \Theta_{0}$ 、
$\large \Theta_{f}$ 的速度位置情况。即我们需要求解出两段多项式 :
$\large \Delta t_{1}$ 与
$\large \Delta t_{2}$ 段的多项式，八个未知数
$\large a$ 。

[统一符号] 其中
$\large \Theta$ 是角度，[
$\large \Theta$ 点]代表角速度，即对
$\large \Theta$ 求导。[
$\large \Theta$ 点点]代表角加速度，即对[
$\large \Theta$ 点]求导。在这里
$\large a_{xy}$ 。
$\large x$ 代表得是这个参数属于第几段（个）多项式，
$\large y$ 代表的是该参数的幂次。举例：
$\large a_{13}$ 代表第二个多项式式子的参数，并且它是立方
$\large a$ ，即第二个多项式的
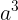
$\large a ^{3}$

一般解法： 由前面的公式：
机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动（一个多项式包含头尾两个方程式）可以直接求解出：
对
$\large \Theta_{0}$ 、
$\large \Theta_{f}$ 求导可以得出角速度
$\large \Theta$ 点：
（注：为了方便运算，在这里我们是假设了一开始和最后的点角速度是0的，该值可以根据实际状况改动。）由于我们要保证我们定义的中间点的位置、速度是连续的，所以要求中间点符合条件：在第一个多项式中，中间点在此可看作“终点” :
$\large \Theta_{1} \left ( t=t_{1} \right )$ ，
$\large \Delta t_{1}$ ∈[
$\large t_{0}$ ,
$\large t_{1}$ ] . 第二个多项式中，中间点在此可看作“起点”:
$\large \Theta_{2} \left ( t=0 \right )$ ，
$\large \Delta t_{2}$ ∈[
$\large t_{1}$ ,
$\large t_{f}$ ] 。为了保证角速度的连续性，要有
$\large \Theta_{1} \left ( t=t_{1} \right )$ 的导数=
$\large \Theta_{2} \left ( t=0 \right )$ 的导数. 为了保证角加速度的连续性，要有
$\large \Theta_{1} \left ( t=t_{1} \right )$ 的导数的导数=
$\large \Theta_{2} \left ( t=0 \right )$ 的导数的导数. 于是有：
机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动（一个中间点能产生速度、加速度两个方程式）联立上面八个等式，就能求解出两个多项式的参数值：
矩阵解法（重点）： 上面的解法转换为矩阵就是：
左式第一个代表第一段多项式的起点，第二个代表终点。左式第三个代表第二段多项式的起点，第四个代表终点。左式第五个代表整个多段式的起点速度，第六个代表终点速度。左式第七个代表第一个中间点的速度连续性条件，第八个代表加速度的条件。有固定套路，记住就好了，下面例题要用的。总结：用多段三次多项式拟合曲线好处是速度、加速度连续，但是需要结合前一段多项式，需要多个式子联立求解就比较麻烦。

广义三次多项式

假设我们有N+1个点，也就是说有N段需要求解的多项式，还表明除了头尾两点，说我们有N-1个中间点。
机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动它的多项式表达式和多段多项式那个一样的，只是表达方式不同了而已，为：
可以看到一个多项式里还是有四个未知数，即我们整体有4N个未知数。由上面多段多项式的例子可知，一个多项式包含头尾两条方程式，由于我们有N个多项式，所以我们就有2N个方程式。而且上面的例子还表明了，一个中间点可以得到两个方程式（速度、加速度），由于我们有N-1个中间点，所以我们就有2（N-1）个方程式。然而此时仅有2N+2（N-1）= 4N-2 个方程，我们的未知数有4N个，还差两条方程式，这样怎么联立求解出未知数？最后两个条件方程式的补充定义方法： 1）定义加速度，头尾加速度都是0，符合真实世界的运动
2）定义速度，按照需求定义头尾的速度情况
（多段多项式的例题就是已经假设了头尾速度为0的情况下） 3）将头尾点看作“中间点”，以达到速度和加速度连续。这一条件针对的是头尾连续，做周期运动的机械臂。
机器人理论（5）轨迹规划：拟合曲线让机械臂连续运动其实广义三次多项式和多段那个一模一样嘛….广义多项式只是扩展了最后两个方程式的定义方法而已….