基础知识

  速度矢量，角速度矢量，叉乘运算   速度是描述质点运动快慢和方向的物理量，等于位移对时间的微分。同时也等于加速度对时间的积分。   角速度： 定义：一个以弧度为单位的圆（一个圆周为2π,即：360度=2π),在单位时间内所走的弧度即为角速度，ω=dφ/dt   角速度的方向垂直于转动平面，可通过右手螺旋定则来确定。 线速度=角速度叉乘半径($v=w\times r$)（由圆心向外指） 根据叉乘的右手法则来规定角速度的方向   叉乘：  
 

刚体的线速度和角速度

线速度

  把坐标系{B} 固连在一刚体上，要求描述相对于坐标系{A} 的运动^B Q 这里已经认为坐标系{A} 是固定的。   坐标系{B} 相对于坐标系{A} 的位置用位置矢量^A P _{B O R G} 和旋转矩阵
来描述。此时，假定方位
不随时间变化，则Q点相对坐标系{A} 的运动是由于^A P _{B O R G} 或^B Q随时间的变化引起的。   求解坐标系{A} 中Q 点的线速度是非常简单的。只要写出坐标系{A} 中的两个速度分量，求其和为：^A V _Q = ^A V _{B O R G} +  
  (1)只适用千坐标系{B}和坐标系{A} 的相对方位保持不变的情况!  

角速度

  如图1两坐标系原点重合且相对线速度为零，固定在坐标系{B}上的矢量^B Q 以角速度 ^A Ω _B 相对于坐标系{A}旋转。那么从{A}看固定在{B}中的矢量随时间变化，可以根据下图分析：  
  从坐标系{B}看矢量Q是不变的：^B V _Q = 0  从坐标系{A}中看点Q的速度为旋转角速度^A Ω _B ​   下图显示了矢量Q绕^A Ω _B ​的旋转，是从坐标系{A}中观测到的  
  可以由图2-3得知：   1、^A Q 的微分增量一定垂直于^A Ω _B ​​和^A Q 2、微分增量的大小为：∣ Δ Q ∣ = ( A Q s i n θ ) ( ∣ A Ω B ∣ Δ t )    又饿了大小和方向，就可以得到矢量积，根据角速度矢量公式有
但是一般情况下Q是相对于坐标系{B}变化的，加上一个分量，可有：  
  紧接着将以上线速度与角速度扩展为坐标系原点不重合的情况，最终可以推导出从坐标系{A}观测坐标系{B}中固定速度矢量的最终普遍表达式：  
 

连杆间的速度传递

  连杆间速度的传递就如同位姿变换一般，可以通过连杆间的推导从基座的速度逐步推导到末端速度   角速度 当两个ω 矢量都是相对于同一个坐标系时，那么这些角速度能够相加。因此，连杆i+l 的角速度就等于连杆i的角速度加上一个由于关节i+ 1 的角速度引起的分量。参照坐标系{i}, 可写成：（实在懒得打公式，直接截图了）  
  其中  
 
  注意：只有当所有速度矢量都变换到相对于通一个坐标系表述时，两个速度矢量才可以相加！   可以带到得到连杆i+1角速度相对于坐标系{i+1}的表达式
  线速度 坐标系{i+ 1} 原点的线速度等于坐标系{i} 原点的线速度加上一个由于连杆i的角速度引起的新的分量。因此有：    
 
 
  要得到连杆3的速度相对于固定坐标系表达式，用旋转矩阵
对其作旋转变换即可  
 

雅克比

  雅克比矩阵是以n个n元函数的偏导数为元素的行列式，事实上，在函数都连续可微（即偏导数都连续）的前提之下，它就是函数组的微分形式下的系数矩阵（即雅可比矩阵）的行列式   在这里表示的是速度的映射，是一个时变线性映射
  在机器人学中，通常使用雅可比将关节速度与操作臂末端的笛卡儿速度联系起来：
  其中Θ 为操作部关节角矢量，v 是笛卡尔速度矢量，对于6关节机器人，雅克比矩阵是6×6阶矩阵，Θ 是6×1维额，⁰ v 也是6×1维，由一个3×1维线速度矢量和一个3×1维角速度矢量组合起来的  
  根据  
可以得到雅克比矩阵：
 
 

力域中的雅克比

  在多维空间中，功是一个力或者力矩矢量与位移矢量的点积，利用虚功原理可知：  
 
  由上式可知，雅克比的转置将作用在手臂上的笛卡尔力映射成了等效关节力矩，当得到相对于坐标系{0}的雅克比矩阵后，可有对坐标系{0}中的力矢量进行变换：
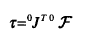  当雅克比矩阵不满秩时，同位置域中的奇异性相同，存在某些特定的方向，末端执行器在这些方向上不能施加期望静态力，在奇异位置，末端笛卡尔施加的力在某些方向上增大或者减小，与所求的关节空间驱动力的值无关  

matlab代码

J = robot.jacob0(q)  %jacob0()求解的是将关节速度映射到世界坐标系中的末端执行器空间速度
Jn = jaconb(q);%末端执行器在自身空间内的速度