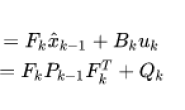导航系统设计专题（四）—扩展卡尔曼滤波（1）_人工智能

前言

上一篇中围绕一个简单的匀速直线运动的状态估计仿真实例展开，阐述了卡尔曼滤波器的实现方式、过程以及仿真效果。本篇将对卡尔曼滤波的几个主要参数的选取作一定的说明，同时，围绕扩展卡尔曼滤波算法展开，阐述其与卡尔曼滤波器的区别与作用。

卡尔曼滤波的参数选取问题

这里还是以上篇中提到的匀速运动仿真实例为案例。

$Q$ 阵为过程噪声矩阵，描述了我们所建立的状态方程的不确定度。例如，仅管我们认为对象处于匀速直线运动状态，然而，现实情况可能如下：

对象在运动过程中遇到上坡，在上坡过程中减速导致状态方程描述的状态量与实际值偏差增大。
对象在运动过程中遇到障碍物，对象减速，导致状态方程描述的状态量与实际值偏差增大。

除了以上描述的两种情况外，还可能存在许多未知的情况，均可能导致状态方程描述不准确的情况。因此，
$Q$ 阵的选定往往代表了我们对于对象在实际运行情况下，状态方程与实际情况的吻合度。若我们认为，状态方程非常可靠，则
$Q$ 阵取较小值，此时，卡尔曼滤波的估计结果更偏向于预测值，反之，则更接近于量测值。

$R$ 阵描述了量测噪声，该矩阵的取值往往由经验决定，可通过传感器厂商给出的Datasheet中找到对应的值，或作为卡尔曼滤波器的可调参数，综合整个滤波器的估计效果来整定。

$P_{0}$

$P_{0}$ 为协方差矩阵的初值，可理解为初始的状态量的不确定度。一般而言，对于精度较低的系统，该值可取一个较大值。

$x_{0}$

$x_{0}$ 为初始状态量，可由一段时间传感器的直接或间接测量值，经过一定的滤波处理或转换计算得到。

卡尔曼滤波与扩展卡尔曼滤波的区别

一定有人会问：既然已经有了卡尔曼滤波算法，那么扩展卡尔曼滤波算法又有何用处？那么，扩展卡尔曼滤波算法究竟解决的是什么样的实际问题？卡尔曼滤波在实际工程中常被用于状态转移矩阵与量测矩阵为线性的情况，原因在于卡尔曼滤波原理是在变量服从高斯分布的前提下推导出来的。当我们将一个高斯分布输入到一个非线性函数中，得到的结果将不符合高斯分布。此时，若强行对非线性对象使用卡尔曼滤波进行状态估计，得到的结果将不再是无偏估计。
导航系统设计专题（四）—扩展卡尔曼滤波（1） 扩展卡尔曼滤波算法（EKF）应运而生。由于被估计对象不再线性，其状态转移矩阵
$F_{k}$ 与量测矩阵
$H_{k}$ 无法再用一个常系数矩阵表示。扩展卡尔曼滤波在每一个更新周期内，针对每一个状态点
$x_{0}$ ，对状态转移矩阵
$F_{k}$ 与量测矩阵
$H_{k}$ 进行泰勒展开：
导航系统设计专题（四）—扩展卡尔曼滤波（1）这里，我们忽略二次以上高阶项，即可得到近似的线性化方程，用于代替非线性函数
$h(x)$ ，即：
将非线性函数
$h(x)$ 拓展到多维，即求各个变量的偏导数，即
其中，对各变量求偏导数所对应的这一项被称为雅可比（Jacobian）项，
导航系统设计专题（四）—扩展卡尔曼滤波（1）所有雅可比项组成了多维雅可比矩阵，而该雅可比矩阵即我们所需要的线性化后的量测矩阵：
线性化后的状态转移矩阵
$F_{k}$ 同理可得，在此不作赘述。在得到线性化后的状态转移矩阵
$F_{k}$ 与量测矩阵
$H_{k}$ 后，我们再次祭出卡尔曼老先生的五大经典卡尔曼滤波方程：