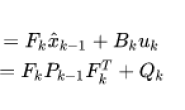前言
上一篇中详细阐述了多旋翼飞行器导航系统中使用的主要传感器及其特性，本篇将着重介绍导航系统设计中常用的两种算法——互补滤波算法与卡尔曼滤波算法。同时，阐述一种多旋翼飞行器导航系统的设计方案。
互补滤波算法简介
互补滤波器的主要原理是把一个主要包含高频噪声，和一个主要包含低频噪声的信号分别通过一个低通滤波器和高通滤波器，并做平均，从而使平均后的结果是真实信号较为准确的估计。简单的讲，就是将两个表征同一个状态信息的观测量分别经过低通/高通滤波器后，将其进行加权，从而使其达到优势互补的效果。 互补滤波器常被用于姿态解算、相对高度的估计等应用。其运算量小，能够在一定程度上解决状态估计的问题。然而，由于其本质上并非最优估计算法。当系统运行环境发生较大变化或出现较大扰动时，其估计精度会大幅下降，这也是其与主流估计算法——卡尔曼滤波之间存在的一个较大区别。下面为采用互补滤波算法的姿态解算流程图。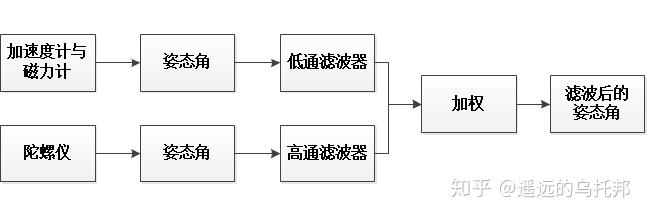 
卡尔曼滤波算法简介
卡尔曼滤波算法是工业领域应用最为广泛的最优估计算法之一。卡尔曼滤波器的作用就是通过降低来自系统本身的误差和环境引起产生的误差，使得我们的估计与预测逼近最优状况。它通过已知的量，去求的隐藏的变量的过程中，需要构建已知量与隐藏变量之间的关系函数，也叫做系统动力方程。但是由于系统本身的误差与系统受环境干扰后产生的误差的原因，实际当中的估计与预测并不会与系统动力方程相符。这里的误差具体来说有三方面：系统误差/测量误差，环境误差/过程误差，估计误差。 测量误差：测量值与真实值之间的差值，测量误差构成测量不确定度： ，表示为字母：
估计误差：估计值与真实值之间的差值，估计误差构成估计不确定度：
，表示为字母：
过程噪音：过程噪音是因外部环境引起的系统不确定性产生的误差，表示为字母：
经典卡尔曼滤波算法的五大方程为：
- 状态更新方程
- 系统动力方程
- 卡尔曼增益方程
- 协方差更新方程
- 协方差外推方程
- 状态更新方程的意义：可以不断更新系统中涉及估计的每个变量，从而逼近变量真实值；系统中涉及的每个变量的最优化，可以使得整个系统接近最优化，最优化到符合构建的系统动力函数。
- 系统动力方程：也叫做状态外推方程，通过构建当前状态与下一状态之间的关系函数来进行随着时间变化的状态推理。系统动力方程本身是由我们已知的变量去推断未知的/隐藏的变量，为此建立的变量之间的关系/函数。
- 卡尔曼增益方程：在推导状态更新方程时，我们将当前本来含有当前状态、第n次测量值的关系式化简成了关于 当前状态、预测状态、卡尔曼增益、第n次测量值 的关系式。由于在通常情况下卡尔曼增益会随着每次迭代发生变化，因此，我们需要更新卡尔曼增益，更新卡尔曼增益就需要清楚的知道，是哪些量组成了卡尔曼增益方程，在前面的学习中我们知道，前一次的估计不确定度与当前的测量不确定度组成了卡尔曼增益方程，并且他们之间有一些关系。
- 估计不确定度更新方程：因为随着每次测量值的不同，卡尔曼增益的不同，我们知道估计不确定度也需要随着每次迭代进行更新。
- 估计不确定度外推方程：估计不确定度不仅要用在卡尔曼增益方程中，也需要用在动力系统方程中，随着估计不确定度外推方程预测下一次估计不确定度。
整个卡尔曼滤波算法的流程如下图所示：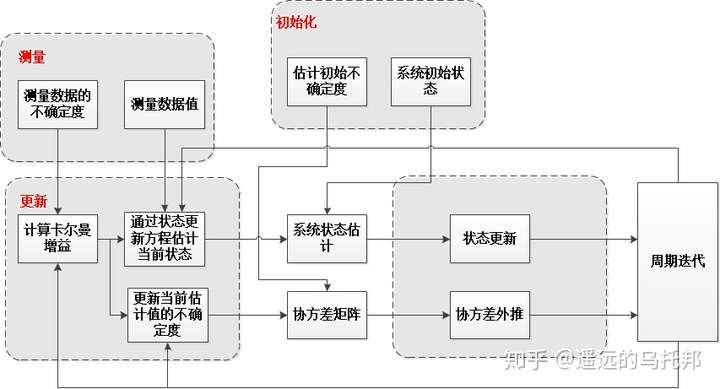 
卡尔曼滤波适用于线性系统，对于非线性系统而言，需要采用扩展卡尔曼滤波，其本质上是卡尔曼滤波算法的一种增广形式，本篇不作赘述。
多旋翼飞行器导航系统设计方案
本篇提供一种切实可行的组合导航系统设计方案，如下图所示：
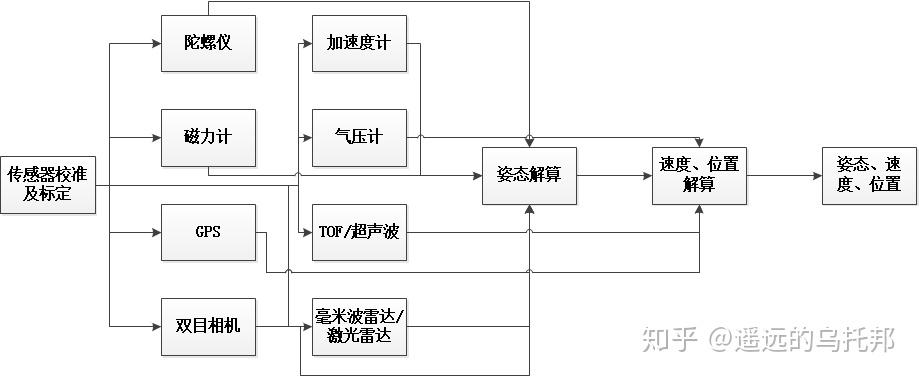
总结
本文对导航系统设计中常用的两种算法——互补滤波算法与卡尔曼滤波算法进行了简介，同时，提出了一种适用于多旋翼飞行器的导航系统设计方案。下一篇中，我们将详解卡尔曼滤波算法原理。
