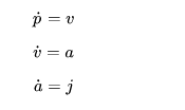前言
上一章介绍了一种高效、实时的运动规划算法——JerkLimitedTrajectory（JLT）。 在给定起始状态与终止状态后，该算法能够快速地计算出一条符合三阶积分器动力学模型的运动轨迹。其适用于类似多旋翼无人机的对象，能够解决一般的运动规划问题。 然而，其存在一定的局限性，如：
- 轨迹平滑度与MAX_JERK之间存在不可调和的矛盾。即很难找到一组参数，使得生成的 轨迹既平滑又快速。
- 其只适用于三阶积分器模型，对于其他非线性模型而言，JLT显得无能为力。
因此，本篇将介绍另外一种通用的运动规划算法——模型预测控制（MPC）。 它既是一种控制算法，也常被应用于解决运动规划问题，如今被广泛应用于自动驾驶/能源等领域。
模型-预测-控制（M-P-C）
所谓模型预测控制，即由模型、预测、控制三大部分组成。
- 模型
这里的模型包含系统模型以及问题模型。 系统模型（System model）指的是被控对象的数学模型，如无人机的运动学模型。无人机的飞行轨迹需要时刻满足该数学模型，由此生成的轨迹才是满足基本的运动学约束关系的。 
然而，仅仅满足运动学约束的轨迹是不够的，我们的业务目标往往还存在其他更多的约束，因此，需要其他模型来表达这些约束，如问题模型。 问题模型（Problem model）描述的是被控对象在目标作业条件下所存在的约束关系的数学模型。如无人机在飞行作业中需要避开障碍物、飞行轨迹需要足够的平滑，节省能量等等，这些都属于问题模型描述的范畴。 
- 预测
在明确系统模型与问题模型后，我们需要求解一个二次规划问题（QP），即在同时满足问题模型与系统模型的前提下，寻找一个使得代价函数最小的最优解。从而，通过最优解与系统模型，对被控对象未来一段时间内的状态量进行预测。 以任意初始状态到零位置、速度、加速度的无人机问题模型为例， 
这里，将最小化无人机的位置误差平方、速度误差平方、加速度误差平方以及加加速度误差平方和作为问题模型的优化目标。 在得到最优的J之后，我们即可通过系统模型向前预测一段时间内的系统状态量，从而生成满足约束条件的最优轨迹。
- 控制
MPC的控制框架如下所示： 
对于用户/业务层设定的优化目标，即上文提到的问题模型，我们通过解二次规划问题（QP）来得到满足约束条件的最优解，从而输出至被控对象；下一周期则通过测量值重新进行优化，得到一个滚动优化的解。 然而，对于某些实时性要求较高的被控对象而言（如无人机），我们往往采用另一种控制框架，这种框架被称为Tube based MPC： 
在这种框架下，我们不直接对被控对象状态量的测量值进行控制，而是对被控对象的数学模型的理论状态量进行优化，而被控对象则采用PID、ADRC等控制器进行控制。由此，MPC的解算频率可以得到大大降低，从而节省大量的算力。 此外，在这种框架中，由于MPC不直接参与被控对象的反馈控制，而是作为被控对象的外环输入。因此，在设计MPC时，我们只需要考虑被控对象的系统模型的不确定性，而不需要考虑环境等外界因素导致的不确定性问题。而环境导致的扰动问题则可以交给形如ADRC算法的做法——通过设计扰动观测器，对被控对象进行前馈补偿的方式来解决。感兴趣的朋友可以参考我的另一篇文章： 遥远的乌托邦：控制系统设计专题（二）——自抗扰控制算法（上）
总结
本篇简介了模型预测控制在多旋翼无人机运动规划上的应用。其实，MPC在其他领域也应用的非常广泛，如自动驾驶、光伏等等。对于不同的被控对象，需要建立不同的系统模型，然后，结合业务指标，设计对应的问题模型。 下一篇将针对多旋翼飞行器的运动规划问题进行详细的推导以及应用解析。 作者简介： 一个被Coding耽误的无人机算法工程师，控制、导航略懂一二，热衷技术，喜欢乒乓、音乐、电影，欢迎交流。 知乎：@遥远的乌托邦 GitHub: https://github.com/DistantUtopiaa 微信公众号：@遥远的乌托邦
