前言
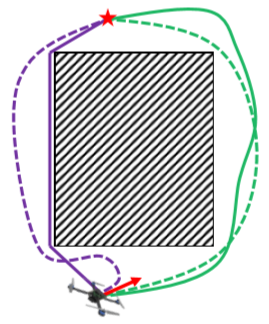

这也是本文重点讨论的基于采样的路径规划算法——状态栅格规划器(State Lattice Planner)。
状态栅格搜索(State Lattice Search)
在构建状态栅格之前,我们需要对被控对象进行运动学分析,即建立对应的运动学模型,这里以简单的无人车模型为例,如下图所示,我们可以将其简化为自行车模型:
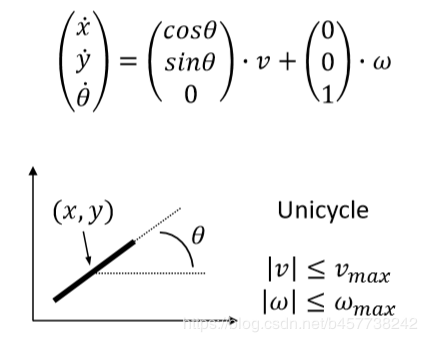
运动学模型主要描述了位置、速度、加速度、转向角度等等状态量在时间上的状态转移,以及对于我们所关心的这些状态量的边界条件进行约束。 在得到被控对象的运动学方程后,我们可以开始正式构建状态栅格,对于State Lattice Search,我们通常有两种采样方式:
- 基于控制空间(Control Space)的采样
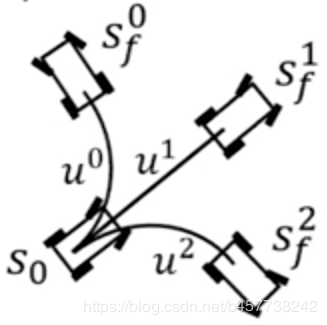
在RRT*算法中,我们对空间中的位置点进行随机采样,那么,在控制空间中,我们应该如何进行采样呢? 很简单,在已知被控对象的情况下,我们固定输入量
(控制量)与积分时间
,由此进行前向积分即可得到被控对象从任意初始状态
过度到的终止状态
,前向积分的方式能够简单粗暴地对被控对象在任意时间
之后的状态进行预测,从而得到一系列状态集合,这就是在控制空间中的采样。 由于输入量
与积分时间
都是任意给定的,因此,基于控制空间的采样往往是没有明确的目的性的,它的采样结果只能分布在某些状态附近,但不能精确地采样到某一个给定状态。

- 基于状态空间(State Space)的采样
而另一种采样方式则是对状态空间的采样。这种采样方式则是在给定被控对象的初始以及目标状态后,反向计算中间过程,相对于前者,该采样方式在工程上较难实施,我们需要对其进行两点边界值问题的求解,才能求得两个状态之间轨迹。
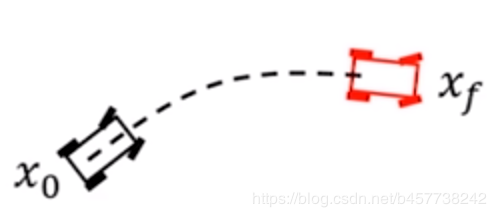
两点边界值问题(BVP)
经典的两点边界值问题,其实就是多项式方程求系数的过程,以多旋翼无人机为例,我们将无人机的状态方程表示为五阶多项式形式,那么,对其状态方程求各阶导数,即可求得位置、速度、加速度等状态量关于时间的表达式,那么,我们只需要将两点边界状态信息代入多项式方程,即可联立求得多项式系数的值,如此一来,一条可通行的轨迹就被解析化了。
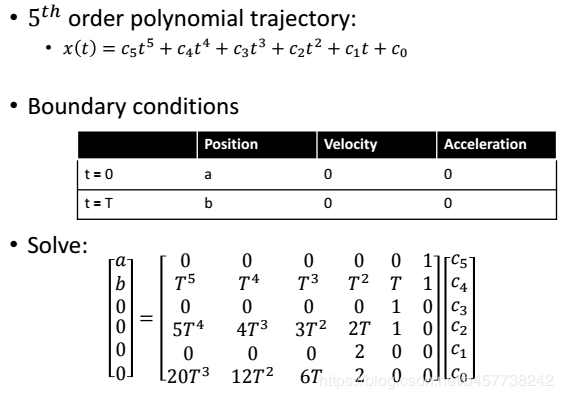
然而,求解BVP问题能够求解一条可通行轨迹,却无法求得一条最优轨迹。或者,当其边界条件部分确定时(如位置确定,速度、加速度状态不确定),需要求解OBVP问题。 OBVP问题可以认为是一个最优控制问题,以多旋翼无人机为例,假设,我们需要最小化无人机在飞行过程中的
,即加加速度,那么可以有以下代价函数
:
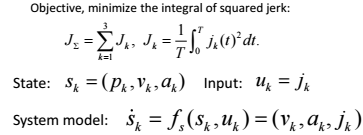
根据Pontryain’s minimum principle,我们可以得到Hamiltonian函数:
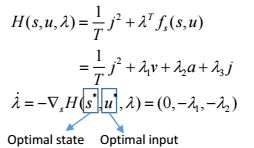
式中
为中间变量,根据极小值原理,可以得到在取得最优输入量
时的最优状态
:

同时,也能够将代价函数
化为关于时间
的函数,那么,我们对于代价函数求极小值即可求得最优的时间
。
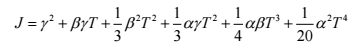
然后,将两点边界状态量代入状态方程,即可得到
、
、
的值,至此,OBVP问题求解完成。
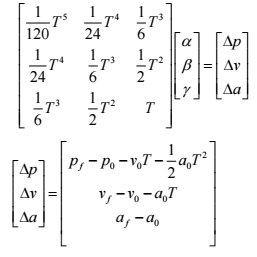
对基于状态空间的采样方法而言,求解OBVP问题即可求得任意两点之间符合运动学方程的最优轨迹。
总结
本篇详细阐述了另一种基于采样的且符合被控对象运动学模型的路径规划算法——State Lattice Planner。 对基于控制空间的采样方式,我们可以很容易地在建立运动学模型的基础上,根据控制输入,对其初始状态进行一定时间
内的前向积分,从而得到一系列符合运动学模型的轨迹;对基于状态空间的采样方式,我们需要求解OBVP问题,有时候,甚至需要对整段轨迹的最优时间
进行优化。 下一篇,我们将针对A*算法的改进型——Hybrid A*进行讨论。
作者简介: 一个被Coding耽误的无人机算法工程师,控制、导航略懂一二,热衷技术,喜欢乒乓、音乐、电影,欢迎交流。 知乎: @遥远的乌托邦 GitHub: https://github.com/DistantUtopia 微信公众号: @遥远的乌托邦





