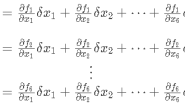一、MPC的力学原理
刚体的力与加速度,转矩与角加速度可以通过牛顿方程和欧拉方程求出:
1、牛顿公式:
基本公式:
 展开形式(n c为与地面接触点的数量):
展开形式(n c为与地面接触点的数量):
 将质量移至右边,可求得加速度:
将质量移至右边,可求得加速度:
 写成更简洁的形式即:
写成更简洁的形式即:

2、欧拉公式
基本公式(ω为角速度,I 为转动惯量):
 对上式做近似考虑:
对上式做近似考虑:
 因此有展开式:
因此有展开式:
 其中:
其中:
 同样将转动惯量移至右边,得到角加速度Θ
同样将转动惯量移至右边,得到角加速度Θ

3、对不同量的参考系作近似变换
为了尽尽可能让系统保持线性关系,同时由于运动过程中滚转角α \alphaα和俯仰角β \betaβ较小,因此有以下近似变换: 角度变换:
 惯量矩阵变换:
惯量矩阵变换:
 绕Z轴的变换的旋转矩阵:
绕Z轴的变换的旋转矩阵:
 Mit实验室给出的cheetah的转动惯量:
Mit实验室给出的cheetah的转动惯量:

4、状态迭代方程
综合公式(1)所计算的加速度 P¨,公式(2)中所计算的角加速度 Θ¨,规定右上标为时刻k ,右下标为所在参考系 各状态量之间的迭代方式如下:
- 旋转角:
 将式(3)~(6)整理写成矩阵形式如下:
将式(3)~(6)整理写成矩阵形式如下:
 (7) 其中:
(7) 其中:

二、构建二次规划问题
1、完整轨迹表示
我们式(7)中的状态迭代方程写成如下形式 :
![]() 其中:
其中:
 此时式(8)是一个线性方程,我们根据其计算未来h步状态:
此时式(8)是一个线性方程,我们根据其计算未来h步状态:
 将上式写成矩阵运算形式:
将上式写成矩阵运算形式:
 现在我们得到了未来h步轨迹的状态矩阵以及其计算表达式(9)
现在我们得到了未来h步轨迹的状态矩阵以及其计算表达式(9)
2、二次规划问题
根据式(9),构造代价函数如下,由轨迹误差项和控制项组成:
 式中L,K分别为权重矩阵(对角矩阵),由于状态X是一个矩阵,安装规范写法,表达如下:
式中L,K分别为权重矩阵(对角矩阵),由于状态X是一个矩阵,安装规范写法,表达如下:
 接下来构造一个二次规划如下(最小化代价函数),该式的物理意义在于,使得计算轨迹尽可能与参考轨迹重合的同时,所使用到的力最小:
接下来构造一个二次规划如下(最小化代价函数),该式的物理意义在于,使得计算轨迹尽可能与参考轨迹重合的同时,所使用到的力最小:
 将式(10)展开,去掉与控制量f无关的项,可化成标准二次型如下:
将式(10)展开,去掉与控制量f无关的项,可化成标准二次型如下:

三、二次规划求解
由于式(12)中数据量比较大,且与机器人系统的配置有关,因此我们从以下简单案例进行讲解: 对于二次多项式: f(x)=2x12+x22+x1x2+x1+x2 求解其在约束条件下的最小值,即为二次规划问题,有以下表达:
 根据约束条件可以得出:
根据约束条件可以得出:
 利用python的cvxopt库可求解该问题:
利用python的cvxopt库可求解该问题:
from cvxopt import matrix, solvers
P = matrix([[4.0, 1.0], [1.0, 2.0]])
q = matrix([1.0, 1.0])
G = matrix([[-1.0, 0.0], [0.0, -1.0]])
h = matrix([0.0, 0.0])
A = matrix([1.0, 1.0], (1, 2))
b = matrix([1.0])
result = solvers.qp(P, q, G, h, A, b)
print('x:\n', result['x'])
结果如下:
pcost dcost gap pres dres
0: 1.8889e+00 7.7778e-01 1e+00 3e-16 2e+00
1: 1.8769e+00 1.8320e+00 4e-02 2e-16 6e-02
2: 1.8750e+00 1.8739e+00 1e-03 2e-16 5e-04
3: 1.8750e+00 1.8750e+00 1e-05 6e-17 5e-06
4: 1.8750e+00 1.8750e+00 1e-07 2e-16 5e-08
Optimal solution found.
x:
[ 2.50e-01]
[ 7.50e-01]