@[toc]
一、初始化特征匹配
1.1 查找候选特征点：
因为单目初始化的两帧是连续的，且初始化的两帧的速度一般不快，两帧差距不大，因此这里的候选关键帧采用最简单的紧邻搜索。如图所示：
假设特征点在Frame1中的位置为A(x,y)。那么Frame2中的候选特征点就在对应坐标的一个半径为r（默认r=100）的圆中查找
/**
* @brief 找到在 以x,y为中心,半径为r的圆形内且金字塔层级在[minLevel, maxLevel]的候选特征点
*
* @param[in] x 特征点坐标x
* @param[in] y 特征点坐标y
* @param[in] r 搜索半径
* @param[in] minLevel 最小金字塔层级
* @param[in] maxLevel 最大金字塔层级
* @param[in] bRight 是否是右图的标志 ORB3新加的
* @return vector<size_t> 返回搜索到的候选匹配点索引
*/
vector<size_t> Frame::GetFeaturesInArea(const float &x, const float &y, const float &r, const int minLevel, const int maxLevel, const bool bRight) const
{
// 存储搜索结果的vector
vector<size_t> vIndices;
vIndices.reserve(N);
float factorX = r;
float factorY = r;
// Step 1 计算半径为r圆左右上下边界所在的网格列和行的id
// 查找半径为r的圆左侧边界所在网格列坐标。这个地方有点绕，慢慢理解下：
// (mnMaxX-mnMinX)/FRAME_GRID_COLS：表示列方向每个网格可以平均分得几个像素（肯定大于1）
// mfGridElementWidthInv=FRAME_GRID_COLS/(mnMaxX-mnMinX) 是上面倒数，表示每个像素可以均分几个网格列（肯定小于1）
// (x-mnMinX-r)，可以看做是从图像的左边界mnMinX到半径r的圆的左边界区域占的像素列数
// 两者相乘，就是求出那个半径为r的圆的左侧边界在哪个网格列中
// 保证nMinCellX 结果大于等于0
// mnMinX是在ComputeImageBounds()中计算的去畸变后的图像边界
const int nMinCellX = max(0,(int)floor((x-mnMinX-factorX)*mfGridElementWidthInv));
// 如果最终求得的圆的左边界所在的网格列超过了设定了上限，那么就说明计算出错，找不到符合要求的特征点，返回空vector
if(nMinCellX>=FRAME_GRID_COLS)
{
return vIndices;
}
// 原理同上计算圆所在的右边界网格列索引
const int nMaxCellX = min((int)FRAME_GRID_COLS-1,(int)ceil((x-mnMinX+factorX)*mfGridElementWidthInv));
// 如果计算出的圆右边界所在的网格不合法，说明该特征点不好，直接返回空vector
if(nMaxCellX<0)
{
return vIndices;
}
//后面的操作也都是类似的，计算出这个圆上下边界所在的网格行的id
const int nMinCellY = max(0,(int)floor((y-mnMinY-factorY)*mfGridElementHeightInv));
if(nMinCellY>=FRAME_GRID_ROWS)
{
return vIndices;
}
const int nMaxCellY = min((int)FRAME_GRID_ROWS-1,(int)ceil((y-mnMinY+factorY)*mfGridElementHeightInv));
if(nMaxCellY<0)
{
return vIndices;
}
// 检查需要搜索的图像金字塔层数范围是否符合要求，防止输入层级<0
//? 疑似bug。(minLevel>0) 后面条件 (maxLevel>=0)肯定成立
//? 改为 const bool bCheckLevels = (minLevel>=0) || (maxLevel>=0);
const bool bCheckLevels = (minLevel>0) || (maxLevel>=0);
// Step 2 遍历圆形区域内的所有网格，寻找满足条件的候选特征点，并将其index放到输出里
for(int ix = nMinCellX; ix<=nMaxCellX; ix++)
{
for(int iy = nMinCellY; iy<=nMaxCellY; iy++)
{
// 获取这个网格内的所有特征点在 Frame::mvKeysUn 中的索引
const vector<size_t> vCell = (!bRight) ? mGrid[ix][iy] : mGridRight[ix][iy];
// 如果这个网格中没有特征点，那么跳过这个网格继续下一个
// 这样通过网格划分的方式加快搜索速度
if(vCell.empty())
continue;
// 如果这个网格中有特征点，那么遍历这个图像网格中所有的特征点
for(size_t j=0, jend=vCell.size(); j<jend; j++)
{
// 根据索引先读取这个特征点
// ORB3新加的 ，Nleft==-1 单目 直接获取去畸变的特征点
// else 双目 根据bRight判断是左图还是右图，因为双目一般都是事先矫正好的，所以这里不需要去畸变的特征点
const cv::KeyPoint &kpUn = (Nleft == -1) ? mvKeysUn[vCell[j]]
: (!bRight) ? mvKeys[vCell[j]]
: mvKeysRight[vCell[j]];
if(bCheckLevels)// 保证给定的搜索金字塔层级>=0
{
// cv::KeyPoint::octave中表示的是从金字塔的哪一层提取的数据
// 保证特征点是在金字塔层级minLevel和maxLevel之间，不是的话跳过
if(kpUn.octave<minLevel)
continue;
if(maxLevel>=0) //? 为何特意又强调？感觉多此一举
if(kpUn.octave>maxLevel)
continue;
}
// 通过检查，计算候选特征点到圆中心的距离，查看是否是在这个圆形区域之内
const float distx = kpUn.pt.x-x;
const float disty = kpUn.pt.y-y;
// 如果x方向和y方向的距离都在指定的半径之内，存储其index为候选特征点
if(fabs(distx)<factorX && fabs(disty)<factorY)
vIndices.push_back(vCell[j]);
}
}
}
return vIndices;
}
1.2 匹配对应的特征点
遍历1.1中的候选特征点，找出描述子汉明距离最小的点，并经过下面三个校验
（1）最小汉明距离<设定的阈值=50；
（2）最小汉明距离<次小汉明距离*0.9；
（3）没有重复匹配，即一个点对应多个点(这样的点，特征区分度不高，而且多重匹配也不知道他到底对应哪个点)
（4）该点的旋转方向和其他点主要的旋转方向一致；
/**
* @brief 单目初始化中用于参考帧和当前帧的特征点匹配
* 步骤
*
* Step 1 在半径窗口内搜索当前帧F2中所有的候选匹配特征点
* Step 2 遍历搜索搜索窗口中的所有潜在的匹配候选点，找到最优的和次优的
* Step 3 对最优次优结果进行检查，满足阈值、最优/次优比例，删除重复匹配
* Step 4 构建旋转直方图，计算匹配点旋转角度差所在的直方图
* Step 5 筛除旋转直方图中“非主流”部分
* Step 6 将最后通过筛选的匹配好的特征点保存
* @param[in] F1=Frame1 初始化参考帧
* @param[in] F2=Frame2 当前帧
* @param[in & out] vbPrevMatched 本来存储的是参考帧的所有特征点坐标，该函数更新为匹配好的当前帧的特征点坐标
* @param[in & out] vnMatches12 保存参考帧F1中特征点是否匹配上，index保存是F1对应特征点索引，值保存的是匹配好的F2特征点索引
* @param[in] windowSize 搜索窗口
* @return int 返回成功匹配的特征点数目
*/
int ORBmatcher::SearchForInitialization(Frame &F1, Frame &F2, vector<cv::Point2f> &vbPrevMatched, vector<int> &vnMatches12, int windowSize)
{
int nmatches=0; // 匹配的特征点个数
// F1中特征点和F2中匹配关系，注意是按照F1特征点数目分配空间
vnMatches12 = vector<int>(F1.mvKeysUn.size(),-1);
// Step 1 构建旋转直方图，HISTO_LENGTH = 30
vector<int> rotHist[HISTO_LENGTH]; // 分成30份，每份360/30=12°
for(int i=0;i<HISTO_LENGTH;i++)
// 每个bin里预分配500个，因为使用的是vector不够的话可以自动扩展容量
rotHist[i].reserve(500);
//! 原作者代码是 const float factor = 1.0f/HISTO_LENGTH; 是错误的，更改为下面代码
const float factor = HISTO_LENGTH/360.0f;
// 匹配点对距离，注意是按照F2特征点数目分配空间
vector<int> vMatchedDistance(F2.mvKeysUn.size(),INT_MAX);
// 从帧2到帧1的反向匹配，注意是按照F2特征点数目分配空间
vector<int> vnMatches21(F2.mvKeysUn.size(),-1);
// 遍历帧1中的所有特征点
for(size_t i1=0, iend1=F1.mvKeysUn.size(); i1<iend1; i1++)
{
cv::KeyPoint kp1 = F1.mvKeysUn[i1];
int level1 = kp1.octave;// 特征点所在的金子塔层级
// 只使用原始图像上提取的特征点
// 这里相当于有一个隐藏条件，就是初始化的两帧的距离间隔不大，因为间隔大的话关键点会在不同的金字塔层级中
if(level1>0)
continue;
// Step 2 在半径窗口内搜索当前帧F2中所有的候选匹配特征点
// vbPrevMatched 输入的是参考帧 F1的特征点
// 圆形windowSize = 100，输入最大最小金字塔层级 均为0
vector<size_t> vIndices2 = F2.GetFeaturesInArea(vbPrevMatched[i1].x,vbPrevMatched[i1].y, windowSize,level1,level1);
// 没有候选特征点，跳过
if(vIndices2.empty())
continue;
// 取出参考帧F1中当前遍历特征点对应的描述子
cv::Mat d1 = F1.mDescriptors.row(i1);
int bestDist = INT_MAX; //最佳描述子匹配距离，越小越好
int bestDist2 = INT_MAX; //次佳描述子匹配距离
int bestIdx2 = -1; //最佳候选特征点在F2中的index
// Step 3 遍历搜索搜索窗口中的所有潜在的匹配候选点，找到最优的和次优的
for(vector<size_t>::iterator vit=vIndices2.begin(); vit!=vIndices2.end(); vit++)
{
size_t i2 = *vit;
// 取出候选特征点对应的描述子
cv::Mat d2 = F2.mDescriptors.row(i2);
// 计算两个特征点描述子距离
int dist = DescriptorDistance(d1,d2);
if(vMatchedDistance[i2]<=dist)
continue;
// 如果当前匹配最佳距离更小，更新最佳次佳距离
if(dist<bestDist)
{
bestDist2=bestDist;
bestDist=dist;
bestIdx2=i2;
}
else if(dist<bestDist2) // 比次佳小，更新次佳
{
bestDist2=dist;
}
}
// Step 4 对最优次优结果进行检查，满足阈值、最优/次优比例，删除重复匹配
// 即使算出了最佳描述子匹配距离，也不一定保证配对成功。要小于设定阈值
if(bestDist<=TH_LOW)
{
// 最佳距离比次佳距离要小于设定的比例，这样特征点辨识度更高
if(bestDist<(float)bestDist2*mfNNratio)
{
// 如果找到的候选特征点对应F1中特征点已经匹配过了，说明发生了重复匹配，将原来的匹配也删掉
if(vnMatches21[bestIdx2]>=0)
{
vnMatches12[vnMatches21[bestIdx2]]=-1;
nmatches--;
}
// 次优的匹配关系，双向建立
vnMatches12[i1]=bestIdx2; // vnMatches12保存参考帧F1和F2匹配关系，index保存是F1对应特征点索引，值保存的是匹配好的F2特征点索引
vnMatches21[bestIdx2]=i1; // 和上面正好相反
vMatchedDistance[bestIdx2]=bestDist;
nmatches++;
// Step 5 计算匹配点旋转角度差所在的直方图
if(mbCheckOrientation)
{
// 计算匹配特征点的角度差，这里单位是角度°，不是弧度
float rot = F1.mvKeysUn[i1].angle-F2.mvKeysUn[bestIdx2].angle;
if(rot<0.0) //使角度范围为[0,360)
rot+=360.0f;
// 前面factor = HISTO_LENGTH/360.0f
// bin = rot / 360.of * HISTO_LENGTH 表示当前rot被分配在第几个直方图bin
int bin = round(rot*factor);
// 如果bin 满了又是一个轮回
if(bin==HISTO_LENGTH)
bin=0;
assert(bin>=0 && bin<HISTO_LENGTH); //校验bin的范围
rotHist[bin].push_back(i1);// 存入对应直方图
}
}
}
}
// 大部分的点的旋转方向应该是一样的，因此旋转方向不同的点就是错误的点
// Step 6 筛除旋转直方图中“非主流”部分
if(mbCheckOrientation)
{
int ind1=-1;
int ind2=-1;
int ind3=-1;
// 筛选出在旋转角度差落在在直方图区间内数量最多的前三个bin的索引
ComputeThreeMaxima(rotHist,HISTO_LENGTH,ind1,ind2,ind3);
for(int i=0; i<HISTO_LENGTH; i++)
{
if(i==ind1 || i==ind2 || i==ind3)
continue;
// 剔除掉不在前三的匹配对，因为他们不符合“主流旋转方向”
for(size_t j=0, jend=rotHist[i].size(); j<jend; j++)
{
int idx1 = rotHist[i][j]; //取出F1中的不满足旋转角度条件的特征点索引，删除他们
if(vnMatches12[idx1]>=0)// 这个判断是因为并不是F1每个特征点都有对应的匹配,因为要计算nmatches
{
vnMatches12[idx1]=-1;
nmatches--;
}
}
}
}
//Update prev matched
// Step 7 将最后通过筛选的匹配好的特征点保存到vbPrevMatched
for(size_t i1=0, iend1=vnMatches12.size(); i1<iend1; i1++)
if(vnMatches12[i1]>=0)//? 理论上这里应该是1
vbPrevMatched[i1]=F2.mvKeysUn[vnMatches12[i1]].pt;
return nmatches;
}
二、计算H矩阵
2.1 H矩阵求解原理
用单应矩阵H_{21}来描述特征点对p_1,p_2之间的变换关系: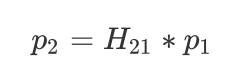
写成矩阵形式: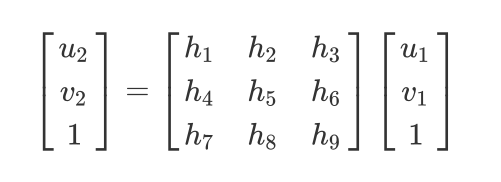
展开计算得到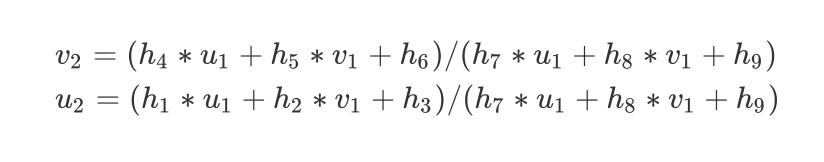
转化为矩阵形式
等式左边两项分别用A, X表示,则有
AX=0
一对点提供两个约束等式,单应矩阵H总共有9个元素,8个自由度(尺度等价性),所以需要4对点提供
8个约束方程就可以求解。
/**
* @brief 用DLT方法求解单应矩阵H
* 这里最少用4对点就能够求出来，不过这里为了统一还是使用了8对点求最小二乘解
*
* @param[in] vP1 参考帧中归一化后的特征点
* @param[in] vP2 当前帧中归一化后的特征点
* @return cv::Mat 计算的单应矩阵H
*/
cv::Mat TwoViewReconstruction::ComputeH21(const vector<cv::Point2f> &vP1, const vector<cv::Point2f> &vP2)
{
// 基本原理：见附件推导过程：
// |x'| | h1 h2 h3 ||x|
// |y'| = a | h4 h5 h6 ||y| 简写: x' = a H x, a为一个尺度因子
// |1 | | h7 h8 h9 ||1|
// 使用DLT(direct linear tranform)求解该模型
// x' = a H x
// ---> (x') 叉乘 (H x) = 0 (因为方向相同) (取前两行就可以推导出下面的了)
// ---> Ah = 0
// A = | 0 0 0 -x -y -1 xy' yy' y'| h = | h1 h2 h3 h4 h5 h6 h7 h8 h9 |
// |-x -y -1 0 0 0 xx' yx' x'|
// 通过SVD求解Ah = 0，A^T*A最小特征值对应的特征向量即为解
// 其实也就是右奇异值矩阵的最后一列
//获取参与计算的特征点的数目
const int N = vP1.size();
// 构造用于计算的矩阵 A
cv::Mat A(2*N, //行，注意每一个点的数据对应两行
9, //列
CV_32F); //float数据类型
// 构造矩阵A，将每个特征点添加到矩阵A中的元素
for(int i=0; i<N; i++)
{
//获取特征点对的像素坐标
const float u1 = vP1[i].x;
const float v1 = vP1[i].y;
const float u2 = vP2[i].x;
const float v2 = vP2[i].y;
//生成这个点的第一行
A.at<float>(2*i,0) = 0.0;
A.at<float>(2*i,1) = 0.0;
A.at<float>(2*i,2) = 0.0;
A.at<float>(2*i,3) = -u1;
A.at<float>(2*i,4) = -v1;
A.at<float>(2*i,5) = -1;
A.at<float>(2*i,6) = v2*u1;
A.at<float>(2*i,7) = v2*v1;
A.at<float>(2*i,8) = v2;
//生成这个点的第二行
A.at<float>(2*i+1,0) = u1;
A.at<float>(2*i+1,1) = v1;
A.at<float>(2*i+1,2) = 1;
A.at<float>(2*i+1,3) = 0.0;
A.at<float>(2*i+1,4) = 0.0;
A.at<float>(2*i+1,5) = 0.0;
A.at<float>(2*i+1,6) = -u2*u1;
A.at<float>(2*i+1,7) = -u2*v1;
A.at<float>(2*i+1,8) = -u2;
}
// 定义输出变量，u是左边的正交矩阵U， w为奇异矩阵，vt中的t表示是右正交矩阵V的转置
cv::Mat u,w,vt;
//使用opencv提供的进行奇异值分解的函数
cv::SVDecomp(A, //输入，待进行奇异值分解的矩阵
w, //输出，奇异值矩阵
u, //输出，矩阵U
vt, //输出，矩阵V^T
cv::SVD::MODIFY_A | //输入，MODIFY_A是指允许计算函数可以修改待分解的矩阵，官方文档上说这样可以加快计算速度、节省内存
cv::SVD::FULL_UV); //FULL_UV=把U和VT补充成单位正交方阵
// 返回最小奇异值所对应的右奇异向量
// 注意前面说的是右奇异值矩阵的最后一列，但是在这里因为是vt，转置后了，所以是行；由于A有9列数据，故最后一列的下标为8
return vt.row(8).reshape(0, //转换后的通道数，这里设置为0表示是与前面相同
3); //转换后的行数,对应V的最后一列
}
2.2 特征点归一化
矩阵A是利用8点法求基础矩阵的关键,所以Hartey就认为,利用8点法求基础矩阵不稳定的一个主要原
因就是原始的图像像点坐标组成的系数矩阵A不好造成的,而造成A不好的原因是像点的齐次坐标各个分
量的数量级相差太大。基于这个原因,Hartey提出一种改进的8点法,在应用8点法求基础矩阵之前,先
对像点坐标进行归一化处理,即对原始的图像坐标做同向性变换,这样就可以减少噪声的干扰,大大的
提高8点法的精度。
==预先对图像坐标进行归一化有以下好处:==
- 能够提高运算结果的精度
- 利用归一化处理后的图像坐标,对任何尺度缩放和原点的选择是不变的。归一化步骤预先为图像坐
标选择了一个标准的坐标系中,消除了坐标变换对结果的影响。
归一化操作分两步进行,首先对每幅图像中的坐标进行平移(每幅图像的平移不同)使图像中匹配的点
组成的点集的质心(Centroid)移动到原点;接着对坐标系进行缩放使得各个方向上的分量总体上有一样的平均值,各个坐标轴的缩放相同的，最后选择合适的缩放因子使点p到原点的平均距离是\sqrt2。 概括起来变换过程如下：
(1) 对点进行平移使其形心位于原点。
(2) 对点进行缩放，使它们到原点的平均距离为\sqrt2
(3) 对两幅图像独立进行上述变换。
具体步骤如下：
（1）对于特征点集合
P=p_1,p_2,…,p_n
(2) 求数学期望（均值）
\bar{u}=E(P)
(3) 求各个方向上的一阶绝对矩，以x方向为例
（==注意这里不是标准差，因为这里的平均距离是$\sqrt2$。标准差对应的距离是1==）
s_x=\sum^N_{i=0}|x_i-\bar{u}|/N
(4)求归一化后的坐标
x’=\frac{x-\bar{u}}{s_x}
(5) 写成变换矩阵
P’=TP
即
/**
* @brief 归一化特征点到同一尺度，作为后续normalize DLT的输入
* [x' y' 1]' = T * [x y 1]'
* 归一化后x', y'的均值为0，sum(abs(x_i'-0))=1，sum(abs((y_i'-0))=1
*
* 为什么要归一化？
* 在相似变换之后(点在不同的坐标系下),他们的单应性矩阵是不相同的
* 如果图像存在噪声,使得点的坐标发生了变化,那么它的单应性矩阵也会发生变化
* 我们采取的方法是将点的坐标放到同一坐标系下,并将缩放尺度也进行统一
* 对同一幅图像的坐标进行相同的变换,不同图像进行不同变换
* 缩放尺度是为了让噪声对于图像的影响在一个数量级上
*
* Step 1 计算特征点X,Y坐标的均值
* Step 2 计算特征点X,Y坐标离均值的平均偏离程度
* Step 3 将x坐标和y坐标分别进行尺度归一化，使得x坐标和y坐标的一阶绝对矩分别为1
* Step 4 计算归一化矩阵：其实就是前面做的操作用矩阵变换来表示而已
*
* @param[in] vKeys 待归一化的特征点
* @param[in & out] vNormalizedPoints 特征点归一化后的坐标
* @param[in & out] T 归一化特征点的变换矩阵
*/
void TwoViewReconstruction::Normalize(const vector<cv::KeyPoint> &vKeys, vector<cv::Point2f> &vNormalizedPoints, cv::Mat &T)
{
// 归一化的是这些点在x方向和在y方向上的一阶绝对矩（随机变量的期望）。
// Step 1 计算特征点X,Y坐标的均值 meanX, meanY
float meanX = 0;
float meanY = 0;
//获取特征点的数量
const int N = vKeys.size();
//设置用来存储归一后特征点的向量大小，和归一化前保持一致
vNormalizedPoints.resize(N);
//开始遍历所有的特征点
for(int i=0; i<N; i++)
{
//分别累加特征点的X、Y坐标
meanX += vKeys[i].pt.x;
meanY += vKeys[i].pt.y;
}
//计算X、Y坐标的均值
meanX = meanX/N;
meanY = meanY/N;
// Step 2 计算特征点X,Y坐标离均值的平均偏离程度 meanDevX, meanDevY，注意不是标准差
float meanDevX = 0;
float meanDevY = 0;
// 将原始特征点减去均值坐标，使x坐标和y坐标均值分别为0
for(int i=0; i<N; i++)
{
vNormalizedPoints[i].x = vKeys[i].pt.x - meanX;
vNormalizedPoints[i].y = vKeys[i].pt.y - meanY;
//累计这些特征点偏离横纵坐标均值的程度
meanDevX += fabs(vNormalizedPoints[i].x);
meanDevY += fabs(vNormalizedPoints[i].y);
}
// 求出平均到每个点上，其坐标偏离横纵坐标均值的程度；将其倒数作为一个尺度缩放因子
meanDevX = meanDevX/N;
meanDevY = meanDevY/N;
float sX = 1.0/meanDevX;
float sY = 1.0/meanDevY;
// Step 3 将x坐标和y坐标分别进行尺度归一化，使得x坐标和y坐标的一阶绝对矩分别为1
// 这里所谓的一阶绝对矩其实就是随机变量到取值的中心的绝对值的平均值（期望）
for(int i=0; i<N; i++)
{
//对，就是简单地对特征点的坐标进行进一步的缩放
vNormalizedPoints[i].x = vNormalizedPoints[i].x * sX;
vNormalizedPoints[i].y = vNormalizedPoints[i].y * sY;
}
// Step 4 计算归一化矩阵：其实就是前面做的操作用矩阵变换来表示而已
// |sX 0 -meanx*sX|
// |0 sY -meany*sY|
// |0 0 1 |
T = cv::Mat::eye(3,3,CV_32F);
T.at<float>(0,0) = sX;
T.at<float>(1,1) = sY;
T.at<float>(0,2) = -meanX*sX;
T.at<float>(1,2) = -meanY*sY;
}
2.3 计算H矩阵分数
原理就是利用加权的重投影误差计算，以95%置信度的卡方分布的置信区间判断内外点，计算所有内点偏离的程度作为分数。
https://www.cnblogs.com/long5683/p/14279885.html
/**
* @brief 对给定的homography matrix打分,需要使用到卡方检验的知识
*
* @param[in] H21 从参考帧到当前帧的单应矩阵
* @param[in] H12 从当前帧到参考帧的单应矩阵
* @param[in] vbMatchesInliers 匹配好的特征点对的Inliers标记
* @param[in] sigma 方差，默认为1
* @return float 返回得分
*/
float TwoViewReconstruction::CheckHomography(const cv::Mat &H21, const cv::Mat &H12, vector<bool> &vbMatchesInliers, float sigma)
{
// 特点匹配个数
const int N = mvMatches12.size();
// Step 1 获取从参考帧到当前帧的单应矩阵的各个元素
const float h11 = H21.at<float>(0,0);
const float h12 = H21.at<float>(0,1);
const float h13 = H21.at<float>(0,2);
const float h21 = H21.at<float>(1,0);
const float h22 = H21.at<float>(1,1);
const float h23 = H21.at<float>(1,2);
const float h31 = H21.at<float>(2,0);
const float h32 = H21.at<float>(2,1);
const float h33 = H21.at<float>(2,2);
// 获取从当前帧到参考帧的单应矩阵的各个元素
const float h11inv = H12.at<float>(0,0);
const float h12inv = H12.at<float>(0,1);
const float h13inv = H12.at<float>(0,2);
const float h21inv = H12.at<float>(1,0);
const float h22inv = H12.at<float>(1,1);
const float h23inv = H12.at<float>(1,2);
const float h31inv = H12.at<float>(2,0);
const float h32inv = H12.at<float>(2,1);
const float h33inv = H12.at<float>(2,2);
// 给特征点对的Inliers标记预分配空间
vbMatchesInliers.resize(N);
// 初始化score值
float score = 0;
// 基于卡方检验计算出的阈值（sigma=1）
// 自由度为2的卡方分布，显著性水平为0.05，对应的临界阈值
const float th = 5.991;
//信息矩阵，方差平方的倒数
const float invSigmaSquare = 1.0/(sigma*sigma);
// Step 2 通过H矩阵，进行参考帧和当前帧之间的双向投影，并计算起加权重投影误差
for(int i=0; i<N; i++)
{
// 一开始都默认为Inlier
bool bIn = true;
// Step 2.1 提取参考帧和当前帧之间的特征匹配点对
const cv::KeyPoint &kp1 = mvKeys1[mvMatches12[i].first];
const cv::KeyPoint &kp2 = mvKeys2[mvMatches12[i].second];
const float u1 = kp1.pt.x;
const float v1 = kp1.pt.y;
const float u2 = kp2.pt.x;
const float v2 = kp2.pt.y;
// Reprojection error in first image
// x2in1 = H12*x2
// Step 2.2 计算 img2 到 img1 的重投影误差
// x1 = H12*x2
// 将图像2中的特征点通过单应变换投影到图像1中
// |u1| |h11inv h12inv h13inv||u2| |u2in1|
// |v1| = |h21inv h22inv h23inv||v2| = |v2in1| * w2in1inv
// |1 | |h31inv h32inv h33inv||1 | | 1 |
// 计算投影归一化坐标
const float w2in1inv = 1.0/(h31inv*u2+h32inv*v2+h33inv); // 等号右边最后一行的倒数
const float u2in1 = (h11inv*u2+h12inv*v2+h13inv)*w2in1inv; // 等号右边第一行*倒数
const float v2in1 = (h21inv*u2+h22inv*v2+h23inv)*w2in1inv;//等号右边第2行*倒数
// 计算重投影误差 = ||p1(i) - H12 * p2(i)||2
const float squareDist1 = (u1-u2in1)*(u1-u2in1)+(v1-v2in1)*(v1-v2in1);
// 加权的重投影误差=重投影误差/sigma^2
// https://www.cnblogs.com/long5683/p/14279885.html
const float chiSquare1 = squareDist1*invSigmaSquare;
// Step 2.3 用阈值标记离群点，内点的话累加得分
if(chiSquare1>th)
bIn = false;
else
score += th - chiSquare1;// 误差越大，得分越低
// Reprojection error in second image
// x1in2 = H21*x1
// 这里和上面一样
// 计算从img1 到 img2 的投影变换误差
// x1in2 = H21*x1
// 将图像2中的特征点通过单应变换投影到图像1中
// |u2| |h11 h12 h13||u1| |u1in2|
// |v2| = |h21 h22 h23||v1| = |v1in2| * w1in2inv
// |1 | |h31 h32 h33||1 | | 1 |
// 计算投影归一化坐标
const float w1in2inv = 1.0/(h31*u1+h32*v1+h33);
const float u1in2 = (h11*u1+h12*v1+h13)*w1in2inv;
const float v1in2 = (h21*u1+h22*v1+h23)*w1in2inv;
const float squareDist2 = (u2-u1in2)*(u2-u1in2)+(v2-v1in2)*(v2-v1in2);
const float chiSquare2 = squareDist2*invSigmaSquare;
if(chiSquare2>th)
bIn = false;
else
score += th - chiSquare2;
if(bIn)
vbMatchesInliers[i]=true;
else
vbMatchesInliers[i]=false;
}
return score;
}
三、 计算F矩阵
3.1 F矩阵求解原理
特征点对p_1,p_2,用基础矩阵F_{21}来描述特征点对之间的变换关系
p_2^TF_{21}p_1=0
我们写成矩阵形式: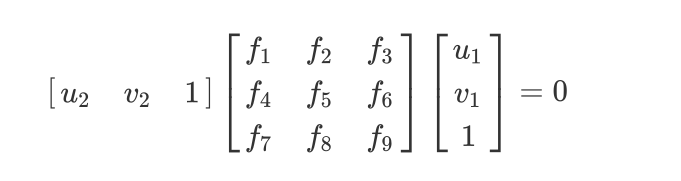
展开得到：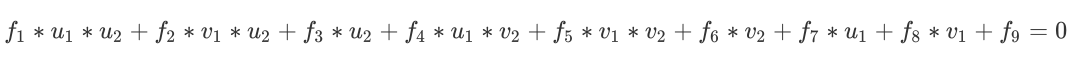
转化为矩阵形式：
等式左边两项分别用A, f表示,则有
Af=0
一对点提供一个约束方程,基础矩阵F总共有9个元素,7个自由度(尺度等价性,本质矩阵E的内在性质秩为2),所以8对点提供8个约束方程就可以求解F。《14讲》P168本质矩阵的性质
/**
* @brief 根据特征点匹配求fundamental matrix（normalized 8点法）
* 注意F矩阵有秩为2的约束，所以需要两次SVD分解
*
* @param[in] vP1 参考帧中归一化后的特征点
* @param[in] vP2 当前帧中归一化后的特征点
* @return cv::Mat 最后计算得到的基础矩阵F
*/
cv::Mat TwoViewReconstruction::ComputeF21(const vector<cv::Point2f> &vP1,const vector<cv::Point2f> &vP2)
{
// 原理详见附件推导
// x'Fx = 0 整理可得：Af = 0
// A = | x'x x'y x' y'x y'y y' x y 1 |, f = | f1 f2 f3 f4 f5 f6 f7 f8 f9 |
// 通过SVD求解Af = 0，A'A最小特征值对应的特征向量即为解
//获取参与计算的特征点对数
const int N = vP1.size();
//初始化A矩阵
cv::Mat A(N,9,CV_32F);// N*9维
for(int i=0; i<N; i++)
{
const float u1 = vP1[i].x;
const float v1 = vP1[i].y;
const float u2 = vP2[i].x;
const float v2 = vP2[i].y;
A.at<float>(i,0) = u2*u1;
A.at<float>(i,1) = u2*v1;
A.at<float>(i,2) = u2;
A.at<float>(i,3) = v2*u1;
A.at<float>(i,4) = v2*v1;
A.at<float>(i,5) = v2;
A.at<float>(i,6) = u1;
A.at<float>(i,7) = v1;
A.at<float>(i,8) = 1;
}
//存储奇异值分解结果的变量
cv::Mat u,w,vt;
// 定义输出变量，u是左边的正交矩阵U， w为奇异矩阵，vt中的t表示是右正交矩阵V的转置
cv::SVDecomp(A,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
// 转换成基础矩阵的形式
cv::Mat Fpre = vt.row(8).reshape(0, 3);// v的最后一列
//基础矩阵的秩为2,而我们不敢保证计算得到的这个结果的秩为2,所以需要通过第二次奇异值分解,来强制使其秩为2
// 对初步得来的基础矩阵进行第2次奇异值分解
cv::SVDecomp(Fpre,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
// 秩2约束，强制将第3个奇异值设置为0
w.at<float>(2)=0;
// 重新组合好满足秩约束的基础矩阵，作为最终计算结果返回
return u*cv::Mat::diag(w)*vt;
}
3.2 特征点归一化
同2.2
3.3 F矩阵秩为2的约束
基础矩阵 F 有个很重要的性质,就是秩为2,可以进一步约束求解准确的F
2.2.1方法使用V^T对应的第9个列向量构造的Fpre 秩通常不为2,我们可以继续进行SVD分解。
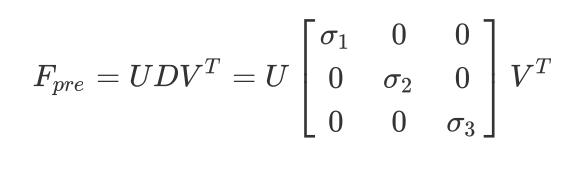
其人为将最小奇异值置为0,这样F矩阵秩为2，重构得到最终的基础矩阵F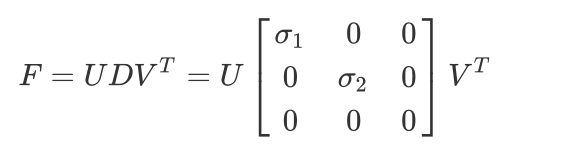
3.4 对极约束与F矩阵分数
与H矩阵使用重投影误差计算分数不同，F矩阵使用点到极线的距离来计算分数
/**
* @brief 对给定的Fundamental matrix打分
*
* @param[in] F21 当前帧和参考帧之间的基础矩阵
* @param[in] vbMatchesInliers 匹配的特征点对属于inliers的标记
* @param[in] sigma 方差，默认为1
* @return float 返回得分
*/
float TwoViewReconstruction::CheckFundamental(const cv::Mat &F21, vector<bool> &vbMatchesInliers, float sigma)
{
// 获取匹配的特征点对的总对数
const int N = mvMatches12.size();
// Step 1 提取基础矩阵中的元素数据
const float f11 = F21.at<float>(0,0);
const float f12 = F21.at<float>(0,1);
const float f13 = F21.at<float>(0,2);
const float f21 = F21.at<float>(1,0);
const float f22 = F21.at<float>(1,1);
const float f23 = F21.at<float>(1,2);
const float f31 = F21.at<float>(2,0);
const float f32 = F21.at<float>(2,1);
const float f33 = F21.at<float>(2,2);
// 预分配空间
vbMatchesInliers.resize(N);
// 设置评分初始值（因为后面需要进行这个数值的累计）
float score = 0;
// 基于卡方检验计算出的阈值
// 自由度为1的卡方分布，显著性水平为0.05，对应的临界阈值
// ?是因为点到直线距离是一个自由度吗？
const float th = 3.841;
// 自由度为2的卡方分布，显著性水平为0.05，对应的临界阈值
const float thScore = 5.991;
// 信息矩阵，或 协方差矩阵的逆矩阵
const float invSigmaSquare = 1.0/(sigma*sigma);
for(int i=0; i<N; i++)
{
//初始默认为这对特征点是Inliers
bool bIn = true;
// Step 2.1 提取参考帧和当前帧之间的特征匹配点对
const cv::KeyPoint &kp1 = mvKeys1[mvMatches12[i].first];
const cv::KeyPoint &kp2 = mvKeys2[mvMatches12[i].second];
// 提取出特征点的坐标
const float u1 = kp1.pt.x;
const float v1 = kp1.pt.y;
const float u2 = kp2.pt.x;
const float v2 = kp2.pt.y;
// Reprojection error in second image
// l2=F21x1=(a2,b2,c2)
// Step 2.2 计算 img1 上的点在 img2 上投影得到的极线 l2 = F21 * p1 = (a2,b2,c2)
// 三个参数对应这直线方程的三个参数 ax+by+c=0
const float a2 = f11*u1+f12*v1+f13;
const float b2 = f21*u1+f22*v1+f23;
const float c2 = f31*u1+f32*v1+f33;
// 理想状态下：x2应该在l这条线上:x2点乘l = 0
// Step 2.3 计算点到直线的距离误差 e = (a * p2.x + b * p2.y + c) / sqrt(a * a + b * b)
const float num2 = a2*u2+b2*v2+c2;
const float squareDist1 = num2*num2/(a2*a2+b2*b2);
// 带权重误差
const float chiSquare1 = squareDist1*invSigmaSquare;
// Step 2.4 误差大于阈值就说明这个点是Outlier
if(chiSquare1>th)
bIn = false;
else // 误差越大，得分越低
score += thScore - chiSquare1;
// Reprojection error in second image
// l1 =x2tF21=(a1,b1,c1)
// 同上，计算img2上的点在 img1 上投影得到的极线 l1= p2^T * F21 = (a1,b1,c1)
const float a1 = f11*u2+f21*v2+f31;
const float b1 = f12*u2+f22*v2+f32;
const float c1 = f13*u2+f23*v2+f33;
// 计算误差 e = (a * p2.x + b * p2.y + c) / sqrt(a * a + b * b)
const float num1 = a1*u1+b1*v1+c1;
const float squareDist2 = num1*num1/(a1*a1+b1*b1);
// 带权重误差
const float chiSquare2 = squareDist2*invSigmaSquare;
if(chiSquare2>th)// 误差大于阈值就说明这个点是Outlier
bIn = false;
else
score += thScore - chiSquare2;
// 双向投影都是内点，才为内点，保存结果
if(bIn)
vbMatchesInliers[i]=true;
else
vbMatchesInliers[i]=false;
}
return score;
}
四、H矩阵恢复相机运动
以下公式出自论文：Motion and structure from motion in a piecewise planar environment
参考了吴博的PPT
我们知道H矩阵对应的3D特征点共面，3维平面可以用下面的公式表示：
aX+bY+cZ=d
即：
n^TP=d
\frac{n^TP}{d}=1
n^T是平面法向量,并指向第一个相机，3D特征点P(x,y,z)为平面上的点。p_1,p_2为两图像上一对对应的特征点。
P_2=RP_1+t
将所有的3D点共平面这个约束引入上式:
\begin{aligned}
p_2&=K(RP_1+t(\frac{n^TP_1}{d})) \
&=K(R+\frac{tn^T}{d})P_1 \
&=K(R+\frac{tn^T}{d})K^{-1}p_1\
&=Hp_1
\end{aligned}
令A=dR+{tn^T}所以
H=K(R+\frac{tn^T}{d})K^{-1}=K\frac{A}{d}K^{-1}
对A矩阵SVD分解：
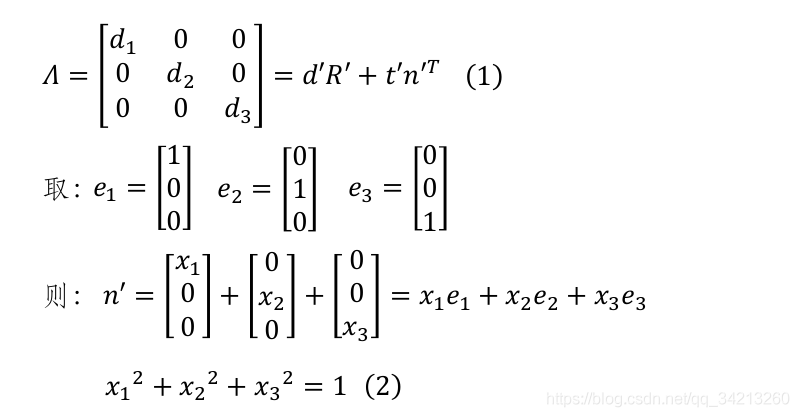
其中(e_1,e_2,e_3)为标准正交基，相当于坐标方向，为了转化为下式：
五、F矩阵恢复相机运动
根据《14讲》，先对本质矩阵进行奇异值分解：
E=U\Sigma V^T
四组解分别为：
t=± 左奇异值矩阵U的最后一列，并对其进行归一化。
R_1=UWV^T
R_2=UW^TV^T
W=R_z^T(\frac{\pi}{2})
六、 三角化出初始的3D地图点
原理分析如下:
匹配特征点对 x，x‘,P，P’分别是投影矩阵,他们将同一个空间点X分别投影到F1和F2的像素坐标上：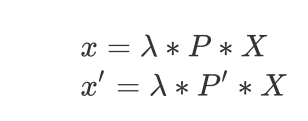
\lambda=\frac{1}{Z}
两个表达式类似,我们以一个通用方程来描述:
为方便推导,简单记为
为了化为齐次方程,左右两边同时叉乘,得到
第三行等于前两行的线性关系，因此只需前两行。同时，因为一对匹配关系有F1，F2两个点所以：
等式左边两项分别用A, X表示,则有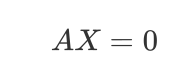
SVD求解,右奇异矩阵的最后一行就是最终的解
/** 给定投影矩阵P1,P2和图像上的匹配特征点点kp1,kp2，从而计算三维点坐标
* @brief
*
* @param[in] kp1 特征点, in reference frame
* @param[in] kp2 特征点, in current frame
* @param[in] P1 投影矩阵P1
* @param[in] P2 投影矩阵P2
* @param[in & out] x3D 计算的三维点
*/
void TwoViewReconstruction::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
{
//这个就是上面注释中的矩阵A
cv::Mat A(4,4,CV_32F);
//构造参数矩阵A
A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);
//奇异值分解的结果
cv::Mat u,w,vt;
//对系数矩阵A进行奇异值分解
cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
//根据前面的结论，奇异值分解右矩阵的最后一行其实就是解，原理类似于前面的求最小二乘解，四个未知数四个方程正好正定
//别忘了我们更习惯用列向量来表示一个点的空间坐标
x3D = vt.row(3).t();
//为了符合其次坐标的形式，使最后一维为1
x3D = x3D.rowRange(0,3)/x3D.at<float>(3);
}
==三角化结果检测==
对每一对特征点三角化，并检测是否满足下面的条件：
（1）三角化出来的3D点（x，y，z）任意一个都不能为无穷大
（2）在两个相机坐标系下的深度值Z都不能为负，两个的视差角要大于0.36°
（3）计算空间点在参考帧和当前帧上的重投影误差，如果大于阈值4*sigma（sigma默认=1）则舍弃。
==H矩阵恢复运动有8组解（F矩阵有4组解），分别对每一组解都进行三角化，能够成功三角化合格点最多的即为最优解。==
同时要满足以下条件，说明三角化成功：
- good点数最优解明显大于次优解，这里H取0.75,F取0.7经验值
- 视角差大于规定的阈值=0.36°
- good点数要大于规定的最小的被三角化的点数量
- good数要足够多，达到所有特征点总数的90%以上
这里的H个F矩阵的条件都是一样的，但是作者的写法有一点不同
参考链接：https://www.cnblogs.com/wangguchangqing/p/8214032.html
开心洋葱 , 版权所有丨如未注明 , 均为原创丨未经授权请勿修改 , 转载请注明ORB_SLAM3原理源码解读系列（2)——单目初始化！
![更加多注释地学习视觉SLAM第九讲程序[1]](https://blog.75271.com/wp-content/themes/com75271/timthumb.php?src=https://blog.75271.com/wp-content/themes/com75271/css/img/pic/9.jpg&h=110&w=185&q=90&zc=1&ct=1)
