最近由于研究机器人的运动控制,所以复习和查阅了一些关于坐标系变换的资料,记录一下,以备使用。
1 空间点的坐标变换
以下公式中,规定几种标识:
1) 坐标系A用{A}表示,同理,有{B};
2) 左上角表示所在坐标系标识,如A p和B p 表示点p分别在坐标系{A}和{B}中的坐标。
1.1 平移坐标变换

1.2 旋转坐标变换
1.3 复合坐标变换

2 旋转矩阵
2.1 二维坐标系的旋转矩阵

2.2 三维坐标系的旋转矩阵
三维坐标系下的旋转需要指定两个要素:旋转轴,旋转角。因此,有不同的旋转矩阵。
2.2.1 绕坐标轴的旋转

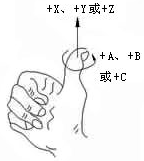
其中θ的方向确定:当旋转轴朝向被观察者时,逆时针旋转为正,即右手系统,右手攥住旋转轴,大拇指指向旋转轴箭头方向时,其它四指指的方向即为旋转正向。如图所示。
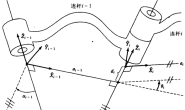
2.2.2 绕空间任意轴的旋转矩阵

θ 的旋转方向也遵守前述的右手系统。
实际上,前面讲的三个绕坐标轴的基本旋转矩阵是以上公式的三个特例。
这个公式也可由以上的三个基本旋转矩阵推导而来,其基本思想是把绕任意单位向量的旋转分解为几个已知的动作:
1) 首先旋转给定向量轴到位于任意一个坐标平面内(XY、YZ或ZX);
2) 然后旋转这个给定向量轴与刚才这个坐标平面内的一个轴重合(X、Y或Z);
3) 利用以上的三个基本旋转矩阵,绕与之重合的这个坐标轴旋转相应的角度θ θθ;
4) 反向做2)步骤的工作;
5) 反向做1)步骤的工作。
具体推导过程可见其它材料。
2.3 旋转矩阵的特性
R T = R − 1 ,即旋转矩阵的转置等于旋转矩阵的逆。旋转矩阵为正交矩阵,同一行、列元素的平方和=1;不同行、列元素对应乘积的和=0;矩阵行列式=1。旋转矩阵的9个元素是线性相关的。
3 多次旋转的组合
一次空间旋转,可以分解为多次旋转的组合,实际上就是多次用不同的旋转矩阵来叉乘,多次旋转矩阵组合时,要注意:矩阵与矩阵的叉乘,或者矩阵与向量的叉乘,满足结合律,但一般不满足交换律,因此,要注意旋转矩阵的顺序。