前段时间周更的vSLAM基础系列突然停更了，也是因为考试周时间不足以让我在看书和写博客之间调剂了。希望朋友们能体谅一下。 
从这周开始会开始更新一个新的栏目就是从零手写VIO。这个没有像视觉SLAM十四讲那样的textbook，so我们就在这个平台一起分享和学习叭~ 视觉 + IMU 融合定位的基础理论和实现：
- IMU 的工作原理和噪声方程
- 视觉与 IMU 紧耦合 的基础理论
- 从零开始实现 VIO 紧耦合优化器（仅基于 Eigen）
VIO概述
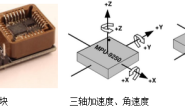
VIO：(Visual-Inertial Odometry) 以视觉与 IMU 融合实现里程计 IMU：(Inertial Measurement Unit)，惯性测量单元
- 典型6轴 IMU 以较高频率（
）返回被测量物体的角速度与加速度
- 受自身温度、零偏、振动等因素干扰，积分得到的平移和旋转容易漂移
加速度计Accelerometer↓ 
陀螺仪Gyroscope↓ 
视觉：(Visual Odometry)
- 以图像形式记录数据，频率较低（
居多）
- 通过图像特征点或像素推断相机运动
是不是发现了两者互补哈~
我就是在记笔记哈哈哈哈！但是不是对PPT的照搬，我虽然会把内容搬下来但是会加入我自己比较通俗的理解。
可利用视觉定位信息来估计 IMU 的零偏，减少 IMU 由零偏导致的发散和累计误差；反之，IMU 可以为视觉提供快速运动时的定位。 松耦合 loose couple：自个算自个的，最后整合数据，是相对独立的；将 IMU 定位与视觉/GNSS 的位姿直接融合，融合过程对两者本身不产生影响，做为后处理方式输出。典型方案为卡尔曼滤波器（Kalman filtering）。 
紧耦合 tightly couple：视觉和 IMU 拉着手，视觉摔翻了（GG了）IMU跟着摔（哈哈哈），就是两者同时用来估计同一个问题。 
IMU 数据可与多种定位方案融合
- 自动驾驶中通常用 IMU+ GPS/差分 GPS/RTK 的融合定位方案，形成 GNSS-INS 组合导航系统，达到厘米组定位精度；
- 头戴式 AR/VR 头盔则多使用视觉 +IMU 的 VIO 定位系统，形成高帧率定位方案。
数学回顾（李群李代数的可以看，不重复写了）
视觉SLAM-从零爬起打破秃头魔咒——（三）李群与李代数 
令 
则有 
- 四元数和矩阵运算类似，如何求
由于 也就是四元数模长的平方，并满足交换律
。
- 3D旋转公式（这里不给出详细证明，Introduction to quaternion里有）
链接:https://pan.baidu.com/share/init?surl=XDqSzbHcmH4PERhMO_t7zA 密码: 6whk 任意向量 沿着以单位向量定义的旋转轴
旋转
度之后的
可以用四元数乘法来获得，令
，
，那么：
- 罗德里格斯公式
之前我写过它的证明： 
- 在VIO中使用右乘扰动模型，之前在十四讲中，常使用的是左乘扰动模型，下面就讲讲为什么用右乘扰动模型的拙见：
首先相机坐标系为 
，世界坐标系为 ，IMU坐标系为
，用
表达并存储IMU的定位信息，
的平移部分.translation()可直接视作IMU在世界中的坐标。 扰动
是IMU在时间
到
相对于W的变换，求导对象
是在时间
时世界坐标系到IMU坐标系的变换，那么
就是
即右乘扰动。
四元数对时间求导
设某个旋转运动的旋转轴为单位向量 ，绕该轴旋转的角度为
，那么对应的单位四元数为：
单位四元数！就是为什么程序里定义四元数要normalize
当旋转一段微小时间，即角度趋于0时，容易有： 
( 当
极小时，
) 其中
表示旋转轴（是用
和单位向量
得出的矢量），模长
标量表示旋转角度。 由于角速度：
四元数时间导数： 
( 其实就是只是实数1，也就是
) 旋转矩阵
关于时间的导数，十四讲中引出李代数时从：
得到 是反对称矩阵令它为
其实我们证明过这个
就是个旋转向量。 使用旋转矩阵
时，角速度为
，那么旋转矩阵
关于时间的导数可写作：
该式成为泊松公式（Possion’s equation），其中
是反对称矩阵算子：
这里我不能确定泊松公式是否和上面的李代数的推导有关，希望有dalao能指点迷津！
左扰动雅可比和右扰动雅可比
- 左扰动雅可比
- 右扰动雅可比
- 旋转连乘的雅克比
BCH的线性表达： 
由于要对 上的微小量
（李代数形式）求导，故要对矩阵做vee(
)和对数运算(
)变成李代数形式，如下：
用到了右乘小量，上面的式(2)，以及 为SO(3)上的右雅可比：
是AngleAxis角轴，
是旋转轴单位向量，
是旋转角也是旋转向量的模。 SO(3)的伴随性质：
求对 旋转连乘的雅克比：
这里能够看到，微小扰动 经过处理，分子上的小量成了
，然而右雅可比仍然是
的李代数构成的角轴形式表达的
。
