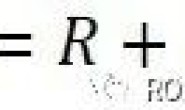我与Robot有个约会——扩展卡尔曼滤波定位

扩展卡尔曼滤波定位是马尔可夫定位中的一种特殊情况，在EKF定位算法中，我们假设地图是由一系列特征组成的，并且每个特征都是独特的。在t时刻的任何一个点，机器人可以通过传感器获得由与附近特征的距离、方向组成的向量： ​ Z_t = {z^1_t, z^2_t,…} 每个测量值z对应一个实际的环境特征c。

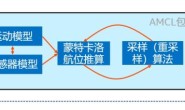
如上图所示，小萝卜头走向1，2，3号门时，下方的置信度都会有所不同。给出2个假设： 1）每个门对应一个label(1,2,3)，测量模型是p(z_t|x_t, m, c_t)，其中m是地图，c_t∈{1,2,3}。 2）假设初始位置已知，置信度值用高斯分布表示，如图a所示；随着机器人向右运动，置信度值会卷积上运动模型，获得一个平移且变宽的高斯分布，如图b所示 接下来，机器人检测到自己在第二个门（c_t = 2）前面，在图c的第一个坐标上表示的就是这次观测 p(z_t|x_t, m, c_t)，同样也是高斯型，与上面求得的置信度值相乘，获得后验概率，如图c第二个坐标系上显示。可以看到，计算获得的置信度值的方差比之前的置信度预测值和测量值都小，高斯曲线更尖陡，这是必须的，因为有两个独立的估计（independent estimates）可以让我们获得更加确信的置信度值。 最后，机器人继续向右移动，由于机器人的运动增加了置信度值的不确定性，使得高斯曲线又变宽了，图d所示。

如上图所示，这是一个基于扩展卡尔曼滤波的（EKF）的传感器融合定位示意图。蓝线是真实轨迹，黑线是航位推测轨迹，绿点是定位观测（例如GPS），红线是用EKF估算的轨迹，红色椭圆是用EKF估算的协方差椭圆。

1.滤波器设计

在仿真中，机器人的状态向量在时刻t处包含4个状态：X_t=[x_t,y_t,ϕ_t,v_t] 其中，x,y 是二维坐标系下的位置，ϕ是朝向，v是速度。 以代码为例：
1）xEst：状态向量 2）P_t: 状态的协方差矩阵 3）Q: 处理噪声时的协方差矩阵 4）R: 时刻t观测噪声的协方差矩阵 机器人有一个速度传感器和陀螺仪传感器，所以输入向量能在每个时刻被用作： ​ u_t = [v_t, w_t] 此外，机器人还有一个GNSS传感器，这意味着机器人可以观察每个时刻的x、y坐标。 ​ z_t = [x_t, y_t] 输入向量和观测向量都包含有传感器噪声。

2.运动模型

机器人模型是
所以，运动模型为： ​ X_t+1 = Fx_t + Bu_t 其中，
d_t 是时间间隔。 参看如下代码：
雅克比矩阵为：

3.观测模型

机器人可以从GPS中获得$xy$位置信息，所以GPS观测模型为：z_t = Hx_t 其中，
它的雅克比矩阵为：

4.扩展卡尔曼滤波

———————————预测————————-

x_pred = Fx_t + Bu_t

P_pred = J_FP_tJ^T_F+Q

———————————更新————————

Z_pred = Hx_pred

y = z- z_pred

S= J_HP_pred.J^T_H + R

K = P_Pred.J^T_HS^-1

x_t+1 = x~pred + Ky

P_t+1 = (I – KJ_H)P~pred

最后总结如下：

当系统为线性高斯模型时，滤波器能给出最优的估计，但是实际系统总是存在不同程度的非线性，如平方、三角关系、开方等。对于非线性系统，可以采用的一种方法是通过线性化方法将非线性系统转换为近似的线性系统，即为EKF，核心思想是：围绕滤波值将非线性函数展开成泰勒级数并略去二阶及以上项，得到一个近似的线性化模型，然后应用卡尔曼滤波完成状态估计。在现今如火如荼的自动驾驶领域，估计汽车的位置和速度，EKF是必不可少的一个环节。