无人机控制之可观性及卡尔曼滤波器_人工智能

1、可观性

1.1、可观性定义

客观性即指通过系统输出能否反映系统初始状态（状态的变化能否由输出反映出来）；形式上如果根据一系列的输出及控制输入可以在有限时间内唯一地确定系统状态则系统客观；其定义中存在三个关键词：动态系统、状态、输出。 举例： 在中医看病中，动态系统为人，望闻问切即为输出，而状态即为人是否生病生了什么病，客观就是由望闻问切的结果推断人的状态；在网络大数据中，动态系统即为网络，状态为要观测出来的有价值信息，输出为能够从网络大数据得到的数据；
无人机控制之可观性及卡尔曼滤波器下图中，很直观地，可得状态A和C是不可观的，状态B和D紧连输出是可观的；

1.2、连续线性系统可观性

（1）线性系统可观测性定义 定义如下一个线性系统
无人机控制之可观性及卡尔曼滤波器线性系统可观测：如果在有限时间间隔
内，根据输出值y(t)和输入值u(t)，能够确定系统的初始状态x(
$t_{0}$ )的每一个分量，那么称此系统是完全可观的，简称可观测。 （2）线性系统可观测性充要条件 定理1：系统
可观测的充分必要条件rank
$O_{v}$ =n； 证明： 将上诉线性系统进行求n-1阶导，可得
无人机控制之可观性及卡尔曼滤波器可构建矩阵运算：
其中只求导阶数至n-1的原因为，根据凯利-哈密尔顿定理：
由上可知
与
$O_{v}$ 秩相同。若rank
$O_{v}$ =n,则可通过求逆求出状态x的唯一解，若小于n存在无穷多解；
无人机控制之可观性及卡尔曼滤波器故证得定理一。 （3）举例 例如：给出两个传感器GPS和加速度计，那么哪一个能够稳定地估计出一维运动小车的速度？为了简化起见，我们用GPS观测位置，一般用如下模型（位置导倒数为速度，速度的导数为一个白噪声）
无人机控制之可观性及卡尔曼滤波器用加速度计估计速度，一般用如下模型：（速度的导数为加速度，加速度的导数为一个白噪声）
上例中，加速度无法得知速度的原因为，未知物体初始速度只知加速度无法确定。

1.3、离散线性系统

（1）定义对于连续线性系统，可以通过采样周期
$T_{s}$ 精确地将连续系统转化成离散系统。将连续系统模型转换成如下离散采样线性系统
无人机控制之可观性及卡尔曼滤波器定义2：如果在有限时间间隔
$NT_{s}$ 内，根据输出值
$y_{k}$ 和外界输入值
$u_{k}$ ，能够确定系统的初始状态
$x_{0}$ 的每一个分量，那么称此系统是完全可观的，简称可观测。 (2)可观性直接解释
无人机控制之可观性及卡尔曼滤波器入连续线性系统进行推导，可得定理

2、卡尔曼滤波器

2.1、卡尔曼滤波器定义

卡尔曼滤波器是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最小方差估计的算法。它的最优估计需满足以下三个条件：（1）无偏性：：即估计值的期望等于状态的真值；
无人机控制之可观性及卡尔曼滤波器（2）估计的方差最小；
（3）实时性。

2.2、卡尔曼滤波器模型推导假设

假设线性离散系统模型如下：
无人机控制之可观性及卡尔曼滤波器式中，过程噪声
$w_{k-1}$ 和观测噪声
$v_{k}$ 的统计特性为
其中
表示过程噪声和观测噪声均值为0，且两者之间独立不相关；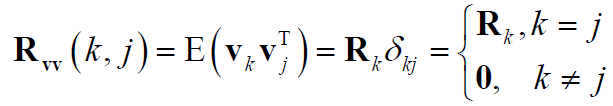
从观测噪声的方差阵可以看出，观测噪声的方差阵R是一个正定矩阵，而非半正定矩阵意味着传感器输出必然含有噪声；初始状态
$x_{0}$ 的统计特性为
补存协方差知识：
无人机控制之可观性及卡尔曼滤波器方差一般是用来描述一维数据的，但现实生活我们常常遇到含有多维数据的数据集，最简单的大家上学时免不了要统计多个学科的考试成绩。协方差就是这样一种用来度量两个随机变量关系的统计量。如果结果为正值，则说明两者是正相关的(从协方差可以引出“相关系数”的定义)，结果为负值就说明负相关的。假设状态的初始值
$x_{0}$ ,
$u_{k}$ 与
$w_{k-1},v_{k}$ 均不相关，并且噪声向量
$w_{k-1},v_{k}$ 也不相关，即有
无人机控制之可观性及卡尔曼滤波器

2.3、卡尔曼滤波器推导思路

目的：假设滤波器形式
其中，
是当前时刻k的最小方差无偏估计（滤波器目标），等号右边包含三个思路：
是上一个·时刻
的最优线性估计（最小方差无偏估计），
为当前输入值，
为上一个我时刻输入值。
为我们模型中所要求得的值。再此基础上进行如下推导：
无人机控制之可观性及卡尔曼滤波器将第一步推导结果带入可得

由以上推导可知，在卡尔曼滤波器中，一方面来自于预测，即
第二方面来自于测量：