本系列文章主要介绍基于A*算法的路径规划的实现,并使用MATLAB进行仿真演示。本文作为本系列的第二篇文章主要介绍如何利用A * 算法进行路径规划。
本系列文章链接:
—————————————————————————–
详细介绍用MATLAB实现基于 A * 算法的路径规划(附完整的代码,代码逐行进行解释)(一)——–A * 算法简介和环境的创建
详细介绍用MATLAB实现基于 A * 算法的路径规划(附完整的代码,代码逐行进行解释)(二)——–利用 A * 算法进行路径规划
详细介绍用MATLAB实现基于 A * 算法的路径规划(附完整的代码,代码逐行进行解释)(三)——–总结及 A * 算法的优化处理
详细介绍用MATLAB实现基于 A * 算法的路径规划(附完整的代码,代码逐行进行解释) (四)——–固定障碍物,进一步对比
—————————————————————————–
四、如何拓展子节点
我们把这部分内容写成一个函数,如下所示:
[costs,heuristics,posinds] = findFValue(setOpen(ii),setOpenCosts(ii), field,goalposind,'euclidean');
1、这个函数的输入参数中setOpen(ii)表示拓展点,setOpenCosts(ii)表示当前拓展点的代价,field是之前生成的环境信息,goalposind是终止点的索引值,euclidean 是拓展的方法(在后面会介绍)
2、这个函数的作用就是把输入的点作为父节点,然后进行拓展找到子节点,并且找到子节点的代价,并且把子节点距离终点的代价找到,函数的输出量中costs表示拓展的子节点到起始点的代价,heuristics表示拓展出来的点到终止点的距离大约是多少,posinds表示拓展出来的子节点
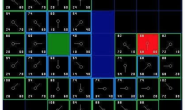
3、在这里介绍一下索引值和坐标值是怎么算的,下图中的红色圆圈的顺序就是索引值的计算顺序,以此类推,蓝色圆圈的顺序就是坐标轴的建立方式,注意无论是坐标值还是索引值他表示的都是方格的左下角的那个点,而不是整个方格,也可以理解为我们用方格的左下角的点来表示该方格


4、现在知道了这个findFValue函数的输出量,输入量,以及这个函数的作用现在就来详细介绍一下这个函数的代码,先摆一下这个函数完整的代码,然后我再逐行解释
function [cost,heuristic,posinds] = findFValue(posind,costsofar,field,goalind,heuristicmethod)
n = length(field); % 获取矩阵的长度
[currentpos(1) currentpos(2)] = ind2sub([n n],posind);
[goalpos(1) goalpos(2)] = ind2sub([n n],goalind);
cost = Inf*ones(4,1); heuristic = Inf*ones(4,1); pos = ones(4,2);
方向一
newx = currentpos(2) - 1; newy = currentpos(1);
if newx > 0
pos(1,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(1) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(1) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(1) = costsofar + field(newy,newx);
end
%方向二
newx = currentpos(2) + 1; newy = currentpos(1);
if newx <= n
pos(2,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(2) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(2) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(2) = costsofar + field(newy,newx);
end
%方向三
newx = currentpos(2); newy = currentpos(1)-1;
if newy > 0
pos(3,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(3) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(3) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(3) = costsofar + field(newy,newx);
end
%方向四
newx = currentpos(2); newy = currentpos(1)+1;
if newy <= n
pos(4,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(4) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(4) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(4) = costsofar + field(newy,newx);
end
posinds = sub2ind([n n],pos(:,1),pos(:,2));
end
5、[currentpos(1) currentpos(2)] = ind2sub([n n],posind)和 [goalpos(1) goalpos(2)] = ind2sub([n n],goalind); 这两条语句分别是将要进行拓展的点(也就是父节点)的索引值拓展成坐标值 、将终止点的索引值拓展成坐标值
6、 cost = Infones(4,1); heuristic = Infones(4,1); pos = ones(4,2); 将矩阵cost和heuristic初始化为4×1的无穷大值的矩阵,pos初始化为4×2的值为1的矩阵,为什么是4×1的呢,因为我们拓展的时候采用的是向上下左右四个方向进行拓展,也就是最多可以找到四个子节点,所以代价矩阵是4×1的,为啥是4×2的呢,因为pos中存放找到的子节点的坐标值,一个子节点需要两个位置,分别存放横纵坐标
7、 因为我们要从要进行拓展的点(也就是父节点)向上下左右四个方向进行尝试,看一下其能否被拓展,成为子节点,也就是在我们得到的目前要进行拓展的点的坐标上对其横坐标+1、-1,纵坐标不变;纵坐标+1、-1,横坐标不变。得到四个方向上相邻的点的横纵坐标newx、newy 也就是接下来四段代码的第一条语句 比如:newx = curren tpos(2) – 1; newy = currentpos(1);因为这四段代码是相似的,就是朝四个方向进行拓展,所以我们已方向一为例来解释,其他三个方向就不啰嗦了
8、接下来 if newx > 0 是用来判断拓展出来的点是否超越了边界,因为我们拓展出来的点一定要在我们之前创建的nxn的环境中,在向下或者向左拓展时要判断其坐标是否大于0,在向上或者向右拓展时要判断是否<=n;
9、pos(1,:) = [newy newx]; 只要拓展出来的这个点没有超出边界就把这个点的坐标值放到pos中
switch lower(heuristicmethod)
case 'euclidean'
heuristic(1) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(1) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
10、 以上代码是用来选择计算终止点距离拓展出来的点代价(或者说距离)的方法,并且计算出终止点距离拓展出来的点的代价(或者说距离)目前两种方法是一样的,后续会进行改进
11、 cost(1) = costsofar + field(newy,newx);就是计算出拓展出来的点距离起始点的代价或者说距离
12、 其他三个方向的代码与此类似,就不啰嗦了,最后一行posinds = sub2ind([n n],pos(:,1),pos(:,2));是将拓展出来的点的坐标值转换成索引值,至此findFValue这个函数就介绍完了
五、利用循环迭代进行路径规划,寻找终止点
1、矩阵的初始化
完成这一个环节,需要用到一些矩阵,我们先对其进行初始化,代码如下:
setOpen = [startposind]; setOpenCosts = [0]; setOpenHeuristics = [Inf];
setClosed = []; setClosedCosts = [];
movementdirections = {'R','L','D','U'}; %移动方向
先来说一下这些矩阵是用来干啥的,setOpen 矩阵是用来存放待选的子节点(也就是拓展出来的子节点)的矩阵,初始化为起始点的索引值,在这个待选的矩阵里面找到最优的值,再存放到矩阵setClosed 中,初始化为空矩阵;setOpenCosts 中存放拓展出来的最优值距离起始点的代价,初始化为0(因为第一个点就是起始点,起始点距离),setOpenHeuristics 中存放待选的子节点距离终止点的代价,movementdirections中存放着四个移动方向的代号
2、调用findFValue函数进行点的拓展
(1)为了方便理解,我们先把变量wallpercent设为0,也就是在没有障碍物的情况下,进行路径规划,类似这种路径规划的算法离不开循环或者迭代,首先要明确在我们没有找到目标的时候就要不停的进行循环或者迭代,直至无路可走或者找到目标
while ~max(ismember(setOpen,goalposind)) && ~isempty(setOpen)
(2) goalposind是之前得到的终止点的索引值,setOpen表示已经拓展出来的点 ismember(setOpen,goalposind)这个函数就是把矩阵setOpen里的点在矩阵goalposind中进行查找,找到了就返回1,找不到返回0,我们看一下MATLAB帮助文档中的例子来理解一下:

(3) setOpen是从起始点开始进行拓展的,若是拓展到了终止点,也就是setOpen中包含终止点,也就是ismember(setOpen,goalposind)的返回值中其中一个元素为1,那么只要我找到了(也就是setopen拓展到了)终止点,max(ismember(setOpen,goal posind))的值就是1,没找到就是0,我们需要在他没找到的时候进行循环所以需要取反一下 ~max(ismember(setOpen,goalposind)) ,此外除了找到终点停止循环,在无路可走时,比如起始点的周围都是障碍物时,也需要停止循环,利用isempty(setOpen) 如果 setOpen为空,isempty(setOpen) 返回逻辑值 1,否则返回逻辑值 0 ,如果setOpen为空表示没有可以拓展的点,也就是无路可走,此时需要跳出循环,因此也需要取反一下: ~ isempty(setOpen) 这两个条件要同时满足,所以将其用&&连起来,也就构成了判断循环的条件 while ~max(ismember(setOpen,goalposind)) && ~isempty(setOpen)
[temp, ii] = min(setOpenCosts + setOpenHeuristics); %寻找拓展出来的最小值
(4) [temp, ii] = min(setOpenCosts + setOpenHeuristics) 函数的返回值ii是(setOpenCosts + setOpenHeuristics)中的最小值在矩阵中的行数 , 返回值 temp是 (setOpen Costs + setOpenHeuristics) 中最小值
[costs,heuristics,posinds] = findFValue(setOpen(ii),setOpenCosts(ii), field,goalposind,'euclidean');
(5)上面这条语句就是调用在第三部分中介绍的findFValue函数来拓展子节点
setClosed = [setClosed; setOpen(ii)];
setClosedCosts = [setClosedCosts; setOpenCosts(ii)];
(6)setClosed = [setClosed; setOpen(ii)];第一次运行这行代码时,setOpen中存放的就是起始点,setClosed为空矩阵,之后再运行时setOpen(ii)就是通过 [temp, ii] = min(setOpenCosts + setOpenHeuristics); 找出来的拓展出来的点中代价最小的那个点 ,然后将其串到矩阵setClosed 中;setClosedCosts = [setClosedCosts; setOpenCosts(ii)];就是将拓展出来的点中代价最小的那个点的代价串到矩阵setClosedCosts
3、从setOpen中删除刚才放到矩阵setClosed中的那个点
(1)刚刚我们已经把拓展出来的子节点(也就是备选点)中最优的那个(当然代价越小,越好,最优的指的就是代价最小的)从setOpen中放到了setClosed ,那为了防止下一次再重复选出这个点,需要将这个点从setOpen中删除,也就是下面这段代码要完成的任务
if (ii > 1 && ii < length(setOpen))
setOpen = [setOpen(1:ii-1); setOpen(ii+1:end)];
setOpenCosts = [setOpenCosts(1:ii-1); setOpenCosts(ii+1:end)];
setOpenHeuristics = [setOpenHeuristics(1:ii-1); setOpenHeuristics(ii+1:end)];
elseif (ii == 1)
setOpen = setOpen(2:end);
setOpenCosts = setOpenCosts(2:end);
setOpenHeuristics = setOpenHeuristics(2:end);
else
setOpen = setOpen(1:end-1);
setOpenCosts = setOpenCosts(1:end-1);
setOpenHeuristics = setOpenHeuristics(1:end-1);
end
(2) if (ii > 1 && ii < length(setOpen)):如果我找到的这个点位于矩阵setOpen的内部(setOpen是个Nx1的矩阵),我要删去第ii个元素,可以通过将这个矩阵的第1到ii-1行与这个矩阵的第ii+1到最后一行进行串联重新生成的这个矩阵就是原来的矩阵删去ii元素,对于setOpen、setOpenCosts 、setOpenHeuristics 这三个矩阵中的该元素都要进行删除操作
(3) elseif (ii == 1):如果这个元素位于矩阵的第一个元素,直接将其第二行到最后一行作为新的矩阵覆盖掉原来的setOpen,这样也就删去了这个元素,同理当这个元素位于最后一行时,直接用setOpen矩阵的第一行到倒数第二行生成的矩阵来覆盖掉原来的矩阵,就相当于删去了这个元素,对于setOpen、setOpenCosts 、setOpenHeuristics 这三个矩阵中的该元素都要进行删除操作
4、把拓展出来的点中符合要求的点放到setOpen 矩阵中,作为待选点
(1)之前我们已经把setOpen 矩阵中待选的子节点中最优的一个放到了setClosed 中,并在setOpen 中对其进行了删除,现在我们需要把拓展出来的点中符合要求的点放到setOpen 矩阵中,也作为待选点,先放一下这一部分的代码:
for jj=1:length(posinds)
if ~isinf(costs(jj))
if ~max([setClosed; setOpen] == posinds(jj))
fieldpointers(posinds(jj)) = movementdirections(jj);
costchart(posinds(jj)) = costs(jj);
setOpen = [setOpen; posinds(jj)];
setOpenCosts = [setOpenCosts; costs(jj)];
setOpenHeuristics = [setOpenHeuristics; heuristics(jj)];
elseif max(setOpen == posinds(jj))
I = find(setOpen == posinds(jj));
if setOpenCosts(I) > costs(jj)
costchart(setOpen(I)) = costs(jj);
setOpenCosts(I) = costs(jj);
setOpenHeuristics(I) = heuristics(jj);
fieldpointers(setOpen(I)) = movementdirections(jj);
end
else
I = find(setClosed == posinds(jj));
if setClosedCosts(I) > costs(jj)
costchart(setClosed(I)) = costs(jj);
setClosedCosts(I) = costs(jj);
fieldpointers(setClosed(I)) = movementdirections(jj);
end
end
end
end
(2)现在我们再来详细解释一下, for jj=1:length(posinds),就是通过循环来一个个处理我们通过findFValue函数拓展出来的点(方格)。 if ~isinf(costs(jj))是判断这个方格处有没有障碍物,如果有障碍物costs中存放的就是inf,isinf(costs(jj))返回就是1,然后取反一下为0,使其不满足if的条件来跳过这个点的处理
(3) 判断完该点(方格)处没有障碍物,还需要判断一下该点是否 已经存在于setOpen 矩阵或者setClosed 矩阵中,如果在这里面的话就先不对这个点进行处理 也就是通过下面这条语句来判断 if ~max([setClosed; setOpen] == posinds(jj)),把setClosed; setOpen拼成一个新的矩阵,然后与存放拓展我们现在要处理的点的矩阵进行对比,如果我们现在要处理的点都不在setClosed或 setOpen中max函数返回的就是0,取反后就是1,进入if语句,执行下面这段程序
fieldpointers(posinds(jj)) = movementdirections(jj);
costchart(posinds(jj)) = costs(jj);
setOpen = [setOpen; posinds(jj)];
setOpenCosts = [setOpenCosts; costs(jj)];
setOpenHeuristics = [setOpenHeuristics; heuristics(jj)];
(4) fieldpointers(posinds(jj)) = movementdirections(jj);就是把移动方向的代号放入之前创建的元胞数组fieldpointers中,costchart(posinds(jj)) = costs(jj);就是把要处理的点的代价存放到矩阵costchart中, setOpen = [setOpen; posinds(jj)]; setOpenCosts = [setOpenCosts; costs(jj)]; setOpenHeuristics = [setOpen Heuristics; heuristics(jj)];就是将拓展点的位置、距离起始点的代价,距离终止点的代价分别串(放到)到矩阵setOpen、 setOpenCosts 、setOpenHeuristics中,这也就意味着这个拓展出来的点的身份正式升级为待选点
(5) 我们已经处理了当我们要处理的拓展点既不在setOpen 矩阵,也不在setClosed 矩阵中的情况,接下来的一段代码就是处理当我们要处理的点已经在setOpen 矩阵中的情况,代码如下:
elseif max(setOpen == posinds(jj))
I = find(setOpen == posinds(jj));
if setOpenCosts(I) > costs(jj)
costchart(setOpen(I)) = costs(jj);
setOpenCosts(I) = costs(jj);
setOpenHeuristics(I) = heuristics(jj);
fieldpointers(setOpen(I)) = movementdirections(jj);
end
(6) elseif max(setOpen == posinds(jj)) 就是用来判断我们要处理的点是否在setOpen 矩阵中,如果在则进入elseif,执行这段代码,I = find(setOpen == pos inds(jj));就是找到要处理的点已经存在于setOpen 矩阵中的位置,返回给变量I, if setOpenCosts(I) > costs(jj) 就是判断我们通过目前的路径拓展出来的这个点要花费的代价和通过之前的路径拓展出这个点话费的代价那个更小,如果之前的更小,也就是之前的路径更好,我们就不对这个点进行处理了,如果现在的更小,也就是说我们通过现在的路径拓展出来的这个点更好,那就把目前这个更小代价去替代之前的代价,也就是这段代码剩下的内容(这几行代码在第一种情况中已经解释过了,在这里就不解释了)
(7)同理可得,接下来,我们需要处理当我们要处理的点已经位于setClosed 矩阵中的情况,原理和方法跟第二种情况一样,所以下面这段代码就不解释了
else
I = find(setClosed == posinds(jj));
if setClosedCosts(I) > costs(jj)
costchart(setClosed(I)) = costs(jj);
setClosedCosts(I) = costs(jj);
fieldpointers(setClosed(I)) = movementdirections(jj);
end
(8)到这里我们就把拓展出来的点中符合要求的点放到setOpen 矩阵中了,接下来的这段代码解释起来比较麻烦就先不解释了,他的作用大概是调整方格的颜色,效果和代码如下所示:
if isempty(setOpen) break; end
set(axishandle,'CData',[costchart costchart(:,end); costchart(end,:) costchart(end,end)]);
% hack to make image look right
set(gca,'CLim',[0 1.1*max(costchart(find(costchart < Inf)))]);
drawnow;

六、通过路径回溯找出规划的路径
1、之前我们已经完成了路径的拓展,接下来就是如何找到我们拓展出来的路径,大体的思路是在我们找到终止点之后,我们去找他是由那个点拓展出来的,也就是找他的父节点,这样不断的回溯,直到回溯到起始点,然后把找到的这些父节点放到一个矩阵中,这个矩阵也就包含了规划出来的路径的信息
2、 先来介绍一下这个findWayBack函数,这个函数的输入参数是终止点和矩阵fieldpointers,输出参数是P,先放一下代码,然后再详细介绍
function p = findWayBack(goalposind,fieldpointers)
n = length(fieldpointers);
posind = goalposind;
[py,px] = ind2sub([n,n],posind);
p = [py px];
while ~strcmp(fieldpointers{posind},'S')
switch fieldpointers{posind}
case 'L' % move left
px = px - 1;
case 'R' % move right
px = px + 1;
case 'U' % move up
py = py - 1;
case 'D' % move down
py = py + 1;
end
p = [p; py px];
posind = sub2ind([n n],py,px);
end
end
3、 矩阵fieldpointers中存放着,拓展的信息,其中S表示起始点,R表示这个点是由右边的点拓展出来的,L表示这个点是由左边的点拓展出来的,U表示这个点是由上面的点拓展出来的,D表示这个点是由下面的点拓展出来的,如下所示:

4、 n = length(fieldpointers); 是 获取矩阵fieldpointers的长度; posind = goalposind;是从终止点开始回溯,把终止点的索引值赋值给变量posind ; [py,px] = ind2sub([n,n],posind);是将posind 的索引值转换成坐标值; p = [py px];就是把装换出来的坐标值赋给变量P(P也就是这个函数的输出参数)
5、接下来就要利用while循环开始回溯了,当我们回溯到起始点的时候停止,也就是在矩阵fieldpointers中找到S时停止,也就是下面的循环条件 while ~strcmp(fieldpo inters{posind},‘S’),其中strcmp(fieldpointers{posind},‘S’)就是比较两个字符是否相等,相等则返回1,也就是找到了起点,然后取反一下,来跳出while循环
6、 switch fieldpointers{posind}就是看一下fieldpointers矩阵当前位置中存放的内容是什么,如果是’L’ 表示当前的点是由左边的点拓展出来的,也就是说当前点的坐标的横坐标-1,纵坐标不变得到的坐标就是他的父节点的坐标也就是两行代码 case ‘L’ px = px – 1;同理其他方向的代码也就理解了
7、 p = [p; py px];就是把找到的这个点的父节点的坐标放到矩阵P中(矩阵P中存放的也就是规划出来的路径上所有点的坐标) posind = sub2ind([n n],py,px);就是把当前找到的父节点的坐标值转换为索引值,继续进行回溯,直至找到起始点,到这里这个函数就介绍完了
8、现在我们已经把我们规划出来路径上点坐标放到了矩阵P中,接下来只需要把这个路径绘制出来就可以了,也就是如下的这段代码所要完成的工作
if max(ismember(setOpen,goalposind))
disp('Solution found!');
p = findWayBack(goalposind,fieldpointers);
plot(p(:,2)+0.5,p(:,1)+0.5,'Color',0.2*ones(3,1),'LineWidth',4);
drawnow;
drawnow;
[y,Fs] = audioread('wee.wav'); sound(y,Fs);
elseif isempty(setOpen)
disp('No Solution!');
[y,Fs] = audioread('pewee-ahh.wav');
sound(y,Fs);
end
9、 if max(ismember(setOpen,goalposind))就是如果setOpen中包含终止点,也就是我们成功找到了从起始点到终止点的路; disp(‘Solution found!’);就是显示字符串Solution found!, p = findWayBack(goalposind,fieldpointers);调用findWayBack函数将规划出来路径上点坐标放到了矩阵P(矩阵P是Nx2的矩阵,每一行分别存储一个点横纵坐标)中, plot(p(:,2)+0.5,p(:,1)+0.5,‘Color’ ,0.2*ones(3,1), ‘LineWidth’,4);就是将P矩阵中相邻的两个点用线连起来(两点确定一条直线)
10、 drawnow:就是将还未处理完的图像实时的显示出来,可以理解为立即执行的plot,变化的plot,当需要反复执行plot时,Matlab程序不会马上把图像画到figure上,这时,要想实时看到图像的每一步变化情况,需要使用这个语句。
11、 [y,Fs] = audioread(‘wee.wav’); sound(y,Fs);是用来干啥的呢,audioread函数用来播放音乐,wee.wav就是要播放的音乐名称,路径跟matlab文件位于同一路径下,放在这就是说我找到了终点,放个音乐庆祝一下…(娱乐性功能…可以删去,读者拿来用的时候别忘了把wee.wav改成你要播放的文件名),下面的[y,Fs] = audioread(‘pewee-ahh.wav’); sound(y,Fs);也是用来放音乐的就不解释了,(clear sound语句可以终止音乐播放)
12、 elseif isempty(setOpen) 就是如果没有找到路径,disp(‘No Solution!’); 显示No Solution!
到这里传统的基于A*算法的路径规划就介绍完了,我感觉这个代码中算法还有一些问题或者说不足之处,我会在后续的文章中介绍对其进行一些优化处理
七、完整的源代码以及我添加了一些中文注释的完整的代码
1、我从网上找的完整的源代码如下:
clc;
clear all;
close all;
%ASTARDEMO Demonstration of ASTAR algorithm
n = 20; % field size n x n tiles
wallpercent = 0.45; % this percent of field is walls
% create the n x n FIELD with wallpercent walls containing movement costs,
% a starting position STARTPOSIND, a goal position GOALPOSIND, the costs
% A star will compute movement cost for each tile COSTCHART,
% and a matrix in which to store the pointers FIELDPOINTERS
[field, startposind, goalposind, costchart, fieldpointers] =initializeField(n,wallpercent);
% initialize the OPEN and CLOSED sets and their costs
setOpen = [startposind]; setOpenCosts = [0]; setOpenHeuristics = [Inf];
setClosed = []; setClosedCosts = [];
movementdirections = {'R','L','D','U'};
% keep track of the number of iterations to exit gracefully if no solution
counterIterations = 1;
% create figure so we can witness the magic
axishandle = createFigure(field,costchart,startposind,goalposind);
% as long as we have not found the goal or run out of spaces to explore
while ~max(ismember(setOpen,goalposind)) && ~isempty(setOpen)
% for the element in OPEN with the smallest cost
[temp, ii] = min(setOpenCosts + setOpenHeuristics);
% find costs and heuristic of moving to neighbor spaces to goal
% in order 'R','L','D','U'
[costs,heuristics,posinds] = findFValue(setOpen(ii),setOpenCosts(ii), ...
field,goalposind,'euclidean');
% put node in CLOSED and record its cost
setClosed = [setClosed; setOpen(ii)];
setClosedCosts = [setClosedCosts; setOpenCosts(ii)];
% update OPEN and their associated costs
if (ii > 1 && ii < length(setOpen))
setOpen = [setOpen(1:ii-1); setOpen(ii+1:end)];
setOpenCosts = [setOpenCosts(1:ii-1); setOpenCosts(ii+1:end)];
setOpenHeuristics = [setOpenHeuristics(1:ii-1); setOpenHeuristics(ii+1:end)];
elseif (ii == 1)
setOpen = setOpen(2:end);
setOpenCosts = setOpenCosts(2:end);
setOpenHeuristics = setOpenHeuristics(2:end);
else
setOpen = setOpen(1:end-1);
setOpenCosts = setOpenCosts(1:end-1);
setOpenHeuristics = setOpenHeuristics(1:end-1);
end
% for each of these neighbor spaces, assign costs and pointers;
% and if some are in the CLOSED set and their costs are smaller,
% update their costs and pointers
for jj=1:length(posinds)
% if cost infinite, then it's a wall, so ignore
if ~isinf(costs(jj))
% if node is not in OPEN or CLOSED then insert into costchart and
% movement pointers, and put node in OPEN
if ~max([setClosed; setOpen] == posinds(jj))
fieldpointers(posinds(jj)) = movementdirections(jj);
costchart(posinds(jj)) = costs(jj);
setOpen = [setOpen; posinds(jj)];
setOpenCosts = [setOpenCosts; costs(jj)];
setOpenHeuristics = [setOpenHeuristics; heuristics(jj)];
% else node has already been seen, so check to see if we have
% found a better route to it.
elseif max(setOpen == posinds(jj))
I = find(setOpen == posinds(jj));
% update if we have a better route
if setOpenCosts(I) > costs(jj)
costchart(setOpen(I)) = costs(jj);
setOpenCosts(I) = costs(jj);
setOpenHeuristics(I) = heuristics(jj);
fieldpointers(setOpen(I)) = movementdirections(jj);
end
% else node has already been CLOSED, so check to see if we have
% found a better route to it.
else
% find relevant node in CLOSED
I = find(setClosed == posinds(jj));
% update if we have a better route
if setClosedCosts(I) > costs(jj)
costchart(setClosed(I)) = costs(jj);
setClosedCosts(I) = costs(jj);
fieldpointers(setClosed(I)) = movementdirections(jj);
end
end
end
end
if isempty(setOpen) break; end
set(axishandle,'CData',[costchart costchart(:,end); costchart(end,:) costchart(end,end)]);
% hack to make image look right
set(gca,'CLim',[0 1.1*max(costchart(find(costchart < Inf)))]);
drawnow;
end
if max(ismember(setOpen,goalposind))
disp('Solution found!');
% now find the way back using FIELDPOINTERS, starting from goal position
p = findWayBack(goalposind,fieldpointers);
% plot final path
plot(p(:,2)+0.5,p(:,1)+0.5,'Color',0.2*ones(3,1),'LineWidth',4);
drawnow;
drawnow;
% celebrate
%[y,Fs] = audioread('wee.wav'); sound(y,Fs);
elseif isempty(setOpen)
disp('No Solution!');
[y,Fs] = audioread('pewee-ahh.wav');
sound(y,Fs);
end
%%
function p = findWayBack(goalposind,fieldpointers)
% This function will follow the pointers from the goal position to the
% starting position
n = length(fieldpointers); % length of the field
posind = goalposind;
% convert linear index into [row column]
[py,px] = ind2sub([n,n],posind);
% store initial position
p = [py px];
% until we are at the starting position
while ~strcmp(fieldpointers{posind},'S')
switch fieldpointers{posind}
case 'L' % move left
px = px - 1;
case 'R' % move right
px = px + 1;
case 'U' % move up
py = py - 1;
case 'D' % move down
py = py + 1;
end
p = [p; py px];
% convert [row column] to linear index
posind = sub2ind([n n],py,px);
end
end
%%
function [cost,heuristic,posinds] = findFValue(posind,costsofar,field, ...
goalind,heuristicmethod)
% This function finds the movement COST for each tile surrounding POSIND in
% FIELD, returns their position indices POSINDS. They are ordered: right,
% left, down, up.
n = length(field); % length of the field
% convert linear index into [row column]
[currentpos(1) currentpos(2)] = ind2sub([n n],posind);
[goalpos(1) goalpos(2)] = ind2sub([n n],goalind);
% places to store movement cost value and position
cost = Inf*ones(4,1); heuristic = Inf*ones(4,1); pos = ones(4,2);
% if we can look left, we move from the right
newx = currentpos(2) - 1; newy = currentpos(1);
if newx > 0
pos(1,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(1) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(1) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(1) = costsofar + field(newy,newx);
end
% if we can look right, we move from the left
newx = currentpos(2) + 1; newy = currentpos(1);
if newx <= n
pos(2,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(2) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(2) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(2) = costsofar + field(newy,newx);
end
% if we can look up, we move from down
newx = currentpos(2); newy = currentpos(1)-1;
if newy > 0
pos(3,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(3) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(3) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(3) = costsofar + field(newy,newx);
end
% if we can look down, we move from up
newx = currentpos(2); newy = currentpos(1)+1;
if newy <= n
pos(4,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(4) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(4) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(4) = costsofar + field(newy,newx);
end
% return [row column] to linear index
posinds = sub2ind([n n],pos(:,1),pos(:,2));
end
%%
function [field, startposind, goalposind, costchart, fieldpointers] = ...
initializeField(n,wallpercent)
% This function will create a field with movement costs and walls, a start
% and goal position at random, a matrix in which the algorithm will store
% f values, and a cell matrix in which it will store pointers
% create the field and place walls with infinite cost
field = ones(n,n) + 10*rand(n,n);
field(ind2sub([n n],ceil(n^2.*rand(n*n*wallpercent,1)))) = Inf;
% create random start position and goal position
startposind = sub2ind([n,n],ceil(n.*rand),ceil(n.*rand));
goalposind = sub2ind([n,n],ceil(n.*rand),ceil(n.*rand));
% force movement cost at start and goal positions to not be walls
field(startposind) = 0; field(goalposind) = 0;
% put not a numbers (NaN) in cost chart so A* knows where to look
costchart = NaN*ones(n,n);
% set the cost at the starting position to be 0
costchart(startposind) = 0;
% make fieldpointers as a cell array
fieldpointers = cell(n,n);
% set the start pointer to be "S" for start, "G" for goal
fieldpointers{startposind} = 'S'; fieldpointers{goalposind} = 'G';
% everywhere there is a wall, put a 0 so it is not considered
fieldpointers(field==inf)={0};
end
% end of this function
%%
function axishandle = createFigure(field,costchart,startposind,goalposind)
% This function creates a pretty figure
% If there is no figure open, then create one
if isempty(gcbf)
figure('Position',[450 50 700 700], ...
'MenuBar','none');
axes('position', [0.01 0.01 0.99 0.99]);
else
% get the current figure, and clear it
gcf; cla;
end
n = length(field);
% plot field where walls are black, and everything else is white
field(field < Inf) = 0;
pcolor(1:n+1,1:n+1,[field field(:,end); field(end,:) field(end,end)]);
% set the colormap for the ploting the cost and looking really nice
cmap = flipud(colormap('jet'));
% make first entry be white, and last be black
cmap(1,:) = zeros(3,1); cmap(end,:) = ones(3,1);
% apply the colormap, but make red be closer to goal
colormap(flipud(cmap));
% keep the plot so we can plot over it
hold on;
% now plot the f values for all tiles evaluated
axishandle = pcolor([1:n+1],[1:n+1],[costchart costchart(:,end); costchart(end,:) costchart(end,end)]);
% plot goal as a yellow square, and start as a green circle
[goalposy,goalposx] = ind2sub([n,n],goalposind);
[startposy,startposx] = ind2sub([n,n],startposind);
plot(goalposx+0.5,goalposy+0.5,'ys','MarkerSize',10,'LineWidth',6);
plot(startposx+0.5,startposy+0.5,'go','MarkerSize',10,'LineWidth',6);
% add a button so that can re-do the demonstration
uicontrol('Style','pushbutton','String','RE-DO', 'FontSize',12, ...
'Position', [1 1 60 40], 'Callback','astardemo');
end
2、我添加了一些中文注释的完整的代码(也就是文章介绍的代码)如下:
%matlab初始化
clc; %清除命令窗口的内容
clear all; %清除工作空间的所有变量,函数,和MEX文件
close all; %关闭所有的figure窗口
%方格数及障碍物比例的设定
n = 40; % 产生一个n x n的方格,修改此值可以修改生成图片的方格数
wallpercent = 0.4; % 这个变量代表生成的障碍物占总方格数的比例 ,如0.5 表示障碍物占总格数的50%
%方格以及障碍物的创建
[field, startposind, goalposind, costchart, fieldpointers] =initializeField(n,wallpercent); %随机生成包含障碍物,起始点,终止点等信息的矩阵
% 路径规划中用到的一些矩阵的初始化
setOpen = [startposind]; setOpenCosts = [0]; setOpenHeuristics = [Inf];
setClosed = []; setClosedCosts = [];
movementdirections = {'R','L','D','U'}; %移动方向
% 这个函数用来随机生成环境,障碍物,起点,终点
axishandle = createFigure(field,costchart,startposind,goalposind); %将随机生成的方格及障碍物的数据生成图像
%%
% 这个while循环是本程序的核心,利用循环进行迭代来寻找终止点
while ~max(ismember(setOpen,goalposind)) && ~isempty(setOpen)
[temp, ii] = min(setOpenCosts + setOpenHeuristics); %寻找拓展出来的最小值
%这个函数的作用就是把输入的点作为父节点,然后进行拓展找到子节点,并且找到子节点的代价,并且把子节点距离终点的代价找到
[costs,heuristics,posinds] = findFValue(setOpen(ii),setOpenCosts(ii), field,goalposind,'euclidean');
setClosed = [setClosed; setOpen(ii)]; % 将找出来的拓展出来的点中代价最小的那个点串到矩阵setClosed 中
setClosedCosts = [setClosedCosts; setOpenCosts(ii)]; % 将拓展出来的点中代价最小的那个点的代价串到矩阵setClosedCosts 中
% 从setOpen中删除刚才放到矩阵setClosed中的那个点
%如果这个点位于矩阵的内部
if (ii > 1 && ii < length(setOpen))
setOpen = [setOpen(1:ii-1); setOpen(ii+1:end)];
setOpenCosts = [setOpenCosts(1:ii-1); setOpenCosts(ii+1:end)];
setOpenHeuristics = [setOpenHeuristics(1:ii-1); setOpenHeuristics(ii+1:end)];
%如果这个点位于矩阵第一行
elseif (ii == 1)
setOpen = setOpen(2:end);
setOpenCosts = setOpenCosts(2:end);
setOpenHeuristics = setOpenHeuristics(2:end);
%如果这个点位于矩阵的最后一行
else
setOpen = setOpen(1:end-1);
setOpenCosts = setOpenCosts(1:end-1);
setOpenHeuristics = setOpenHeuristics(1:end-1);
end
%%
% 把拓展出来的点中符合要求的点放到setOpen 矩阵中,作为待选点
for jj=1:length(posinds)
if ~isinf(costs(jj)) % 判断该点(方格)处没有障碍物
% 判断一下该点是否 已经存在于setOpen 矩阵或者setClosed 矩阵中
% 如果我们要处理的拓展点既不在setOpen 矩阵,也不在setClosed 矩阵中
if ~max([setClosed; setOpen] == posinds(jj))
fieldpointers(posinds(jj)) = movementdirections(jj);
costchart(posinds(jj)) = costs(jj);
setOpen = [setOpen; posinds(jj)];
setOpenCosts = [setOpenCosts; costs(jj)];
setOpenHeuristics = [setOpenHeuristics; heuristics(jj)];
% 如果我们要处理的拓展点已经在setOpen 矩阵中
elseif max(setOpen == posinds(jj))
I = find(setOpen == posinds(jj));
% 如果通过目前的方法找到的这个点,比之前的方法好(代价小)就更新这个点
if setOpenCosts(I) > costs(jj)
costchart(setOpen(I)) = costs(jj);
setOpenCosts(I) = costs(jj);
setOpenHeuristics(I) = heuristics(jj);
fieldpointers(setOpen(I)) = movementdirections(jj);
end
% 如果我们要处理的拓展点已经在setClosed 矩阵中
else
I = find(setClosed == posinds(jj));
% 如果通过目前的方法找到的这个点,比之前的方法好(代价小)就更新这个点
if setClosedCosts(I) > costs(jj)
costchart(setClosed(I)) = costs(jj);
setClosedCosts(I) = costs(jj);
fieldpointers(setClosed(I)) = movementdirections(jj);
end
end
end
end
%%
if isempty(setOpen) break; end
set(axishandle,'CData',[costchart costchart(:,end); costchart(end,:) costchart(end,end)]);
set(gca,'CLim',[0 1.1*max(costchart(find(costchart < Inf)))]);
drawnow;
end
%%
%调用findWayBack函数进行路径回溯,并绘制出路径曲线
if max(ismember(setOpen,goalposind))
disp('Solution found!');
p = findWayBack(goalposind,fieldpointers); % 调用findWayBack函数进行路径回溯,将回溯结果放于矩阵P中
plot(p(:,2)+0.5,p(:,1)+0.5,'Color',0.2*ones(3,1),'LineWidth',4); %用 plot函数绘制路径曲线
drawnow;
drawnow;
[y,Fs] = audioread('000.wav'); sound(y,Fs); % 播放名为000的音乐,注意该文件需要跟matlab文件位于同一文件夹下,
elseif isempty(setOpen)
disp('No Solution!');
[y,Fs] = audioread('000.wav');
sound(y,Fs);
end
%%
%findWayBack函数用来进行路径回溯,这个函数的输入参数是终止点goalposind和矩阵fieldpointers,输出参数是P
function p = findWayBack(goalposind,fieldpointers)
n = length(fieldpointers); % 获取环境的长度也就是n
posind = goalposind;
[py,px] = ind2sub([n,n],posind); % 将索引值posind转换为坐标值 [py,px]
p = [py px];
%利用while循环进行回溯,当我们回溯到起始点的时候停止,也就是在矩阵fieldpointers中找到S时停止
while ~strcmp(fieldpointers{posind},'S')
switch fieldpointers{posind}
case 'L' % ’L’ 表示当前的点是由左边的点拓展出来的
px = px - 1;
case 'R' % ’R’ 表示当前的点是由右边的点拓展出来的
px = px + 1;
case 'U' % ’U’ 表示当前的点是由上面的点拓展出来的
py = py - 1;
case 'D' % ’D’ 表示当前的点是由下边的点拓展出来的
py = py + 1;
end
p = [p; py px];
posind = sub2ind([n n],py,px);% 将坐标值转换为索引值
end
end
%%
%这个函数的作用就是把输入的点作为父节点,然后进行拓展找到子节点,并且找到子节点的代价,并且把子节点距离终点的代价找到。
%函数的输出量中costs表示拓展的子节点到起始点的代价,heuristics表示拓展出来的点到终止点的距离大约是多少,posinds表示拓展出来的子节点
function [cost,heuristic,posinds] = findFValue(posind,costsofar,field,goalind,heuristicmethod)
n = length(field); % 获取矩阵的长度
[currentpos(1) currentpos(2)] = ind2sub([n n],posind); %将要进行拓展的点(也就是父节点)的索引值拓展成坐标值
[goalpos(1) goalpos(2)] = ind2sub([n n],goalind); %将终止点的索引值拓展成坐标值
cost = Inf*ones(4,1); heuristic = Inf*ones(4,1); pos = ones(4,2); %将矩阵cost和heuristic初始化为4x1的无穷大值的矩阵,pos初始化为4x2的值为1的矩阵
% 拓展方向一
newx = currentpos(2) - 1; newy = currentpos(1);
if newx > 0
pos(1,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(1) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(1) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(1) = costsofar + field(newy,newx);
end
% 拓展方向二
newx = currentpos(2) + 1; newy = currentpos(1);
if newx <= n
pos(2,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(2) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(2) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(2) = costsofar + field(newy,newx);
end
% 拓展方向三
newx = currentpos(2); newy = currentpos(1)-1;
if newy > 0
pos(3,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(3) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(3) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(3) = costsofar + field(newy,newx);
end
% 拓展方向四
newx = currentpos(2); newy = currentpos(1)+1;
if newy <= n
pos(4,:) = [newy newx];
switch lower(heuristicmethod)
case 'euclidean'
heuristic(4) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
case 'taxicab'
heuristic(4) = abs(goalpos(2)-newx) + abs(goalpos(1)-newy);
end
cost(4) = costsofar + field(newy,newx);
end
posinds = sub2ind([n n],pos(:,1),pos(:,2)); % 将拓展出来的子节点的坐标值转换为索引值
end
%%
%这个矩阵的作用就是随机生成环境,障碍物,起始点,终止点等
function [field, startposind, goalposind, costchart, fieldpointers] = initializeField(n,wallpercent)
field = ones(n,n) + 10*rand(n,n);%生成一个n*n的单位矩阵+0到10范围内的一个随机数
field(ind2sub([n n],ceil(n^2.*rand(n*n*wallpercent,1)))) = Inf;%向上取整
% 随机生成起始点和终止点
startposind = sub2ind([n,n],ceil(n.*rand),ceil(n.*rand)); %随机生成起始点的索引值
goalposind = sub2ind([n,n],ceil(n.*rand),ceil(n.*rand)); %随机生成终止点的索引值
field(startposind) = 0; field(goalposind) = 0; %把矩阵中起始点和终止点处的值设为0
costchart = NaN*ones(n,n);%生成一个nxn的矩阵costchart,每个元素都设为NaN。就是矩阵初始NaN无效数据
costchart(startposind) = 0;%在矩阵costchart中将起始点位置处的值设为0
% 生成元胞数组
fieldpointers = cell(n,n);%生成元胞数组n*n
fieldpointers{startposind} = 'S'; fieldpointers{goalposind} = 'G'; %将元胞数组的起始点的位置处设为 'S',终止点处设为'G'
fieldpointers(field==inf)={0};
end
% end of this function
%%
%利用随机生成的环境数据来进行环境的绘制
function axishandle = createFigure(field,costchart,startposind,goalposind)
% 这个if..else结构的作用是判断如果没有打开的figure图,则按照相关设置创建一个figure图
if isempty(gcbf) %gcbf是当前返回图像的句柄,isempty(gcbf)假如gcbf为空的话,返回的值是1,假如gcbf为非空的话,返回的值是0
figure('Position',[460 65 700 700], 'MenuBar','none'); %对创建的figure图像进行设置,设置其距离屏幕左侧的距离为450,距离屏幕下方的距离为50,长度和宽度都为700,并且关闭图像的菜单栏
axes('position', [0.01 0.01 0.99 0.99]); %设置坐标轴的位置,左下角的坐标设为0.01,0.01 右上角的坐标设为0.99 0.99 (可以认为figure图的左下角坐标为0 0 ,右上角坐标为1 1 )
else
gcf; cla; %gcf 返回当前 Figure 对象的句柄值,然后利用cla语句来清除它
end
n = length(field); %获取矩阵的长度,并赋值给变量n
field(field < Inf) = 0; %将fieid矩阵中的随机数(也就是没有障碍物的位置处)设为0
pcolor(1:n+1,1:n+1,[field field(:,end); field(end,:) field(end,end)]);%多加了一个重复的(由n X n变为 n+1 X n+1 )
cmap = flipud(colormap('jet')); %生成的cmap是一个256X3的矩阵,每一行的3个值都为0-1之间数,分别代表颜色组成的rgb值
cmap(1,:) = zeros(3,1); cmap(end,:) = ones(3,1); %将矩阵cmap的第一行设为0 ,最后一行设为1
colormap(flipud(cmap)); %进行颜色的倒转
hold on;
axishandle = pcolor([1:n+1],[1:n+1],[costchart costchart(:,end); costchart(end,:) costchart(end,end)]); %将矩阵costchart进行拓展,插值着色后赋给axishandle
[goalposy,goalposx] = ind2sub([n,n],goalposind);
[startposy,startposx] = ind2sub([n,n],startposind);
plot(goalposx+0.5,goalposy+0.5,'ys','MarkerSize',10,'LineWidth',6);
plot(startposx+0.5,startposy+0.5,'go','MarkerSize',10,'LineWidth',6);
%uicontrol('Style','pushbutton','String','RE-DO', 'FontSize',12, 'Position', [1 1 60 40], 'Callback','astardemo');
end
本篇文章到这里就结束了,欢迎大家继续阅读本系列文章的后续文章,本文介绍的内容的完整代码的MATLAB文件我会放到附件里,听说在上传的时候设为粉丝可下载是不需要花费积分的,大家看一下需不需要积分,若还是需要积分,在评论区留言,我直接传给你 本篇文章内容的附件链接:A星算法路径规划博文附件 (https://download.csdn.net/download/qq_44339029/12889832) 欢迎大家积极交流,本文未经允许谢绝转载