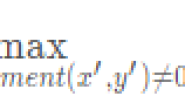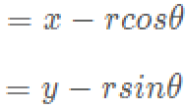数字图像处理(三) 图像的变换

本节主要目的是介绍本书所用到的数字图像的变换，方便之后的处理。来源于东北大学 魏颖教授的数字图像课程笔记。  

傅里叶变换

  信号处理方法有：时域分析法和频域分析法。   频率通常是指某个一维物理量随时间变化快慢程度的度量。   图像是二维信号，其坐标轴是二维空间坐标轴，图像本身所在的域称为空间域（Space Domain）。   图像灰度值随空间坐标变化的快慢也用频率来度量，称为空间频率（Spatial Frequency）。    
   

• 傅立叶变换与时频分析

  人类视觉所感受到的是在空间域和时间域的信号。但是，往往许多问题在频域中讨论时，有其非常方便分析的一面。   我们知道，任何复杂的周期信号$f(t)$可以用简单的调和振荡函数表示成如下形式：  
 
   

• 连续函数的傅立叶变换

  当一个一维信号$f(x)$满足狄里赫莱条件，即$f(x)$：   （1） 具有有限个间断点；（2） 具有有限个极值点；（3） 绝对可积。   则其傅立叶变换对（傅立叶变换和逆变换）一定存在。在实际应用中，这些条件一般总是可以满足的。   一维傅立叶变换对的定义为：  
 
 
  一维傅立叶变换可以很容易地推广到二维，如果二维函数$f(x,y)$满足狄里赫莱条件，则它的二维傅立叶变换对为：  
 
   

• 离散傅立叶变换:

  在数字图像处理中应用傅立叶变换， 还需要解决两个问题：   一是在数学中进行傅立叶变换的$f(x)$为连续（模拟）信号，而计算机处理的是数字信号（图像数据）；二是数学上采用无穷大概念，而计算机只能进行有限次计算。   计 算机能运算的傅立叶变 换 称为离散傅立叶变换（ Discrete FourierTransform，DFT)。   设$\{f(x)|f(0),f(1),f(2),\dots ,f(N-1)\}$为一维信号f ( x ) 的N个抽样， 其离散傅立叶变换对为  
  可见，离散序列的傅立叶变换仍是一个离散的序列，每一个u对应的傅立叶变换结果是所有输入序列f ( x ) 的加权和（每一$f(x)$都乘以不同频率的正弦和余弦值），u 决定了每个傅立叶变换结果的频率。   通常傅立叶变换为复数形式， 即  
  式中：u , x = 0 , 1 , 2 , … , M − 1 ；v， y = 0 , 1 , 2 , … , N − 1 ；$x$,$y$为时域变量，$u$,$v$为频域变量。像一维离散傅立叶变换一样，系数1/MN可以在正变换或逆变换中，也可以在正变换和逆变换前分别乘以系数 ，只要两式系数的乘积等于1／MN即可。   Fourier变换有两个好处：1）可以得出信号在各个频率点上的强度。2）可以将卷积运算化为乘积运算。  

• 图像频域处理的理论基础

  卷积理论   1.被处理图像f(x,y); 2.变换函数h(x,y) /*线性、位置无关操作; 3.目标图像g(x,y);   有卷积：g(x,y) = h(x,y) * f(x,y);有等式：$G(u,v)=H(u,v)F(u,v)$;有等式：g(x,y)=F−1[H(u,v)F(u,v)]。   傅里叶变换   利用傅里叶变换的特性，将时间信号正变换到频率域后进行处理（例如低通、高通或带通），然后再反变换成时间信号，即可完成对信号的滤波。   低通滤波：在频率域中抑制高频信号; 高通滤波：在频率域中抑制低频信号   二维离散函数的傅立叶频谱、 相位谱和能量谱分别为:  
  二维离散傅立叶变换的性质:  
 
 

1. 可分离性

  一个二维傅立叶变换可分解为两步进行， 其中每一步都是一个一维傅立叶变换。先对$f(x,y)$按行进行傅立叶变换得到$F(x,v)$，再对F ( x , v ) 按列进行傅立叶变换，便可得到f ( x , y )的傅立叶变换结果。显然对f ( x , y ) 先按列进行离散傅立叶变换， 再按行进行离散傅立叶变换也是可行的。  
 

2. 平移性质

 
 
  平移性质表明，只要将$f(x,y)$乘以因子 (－1)^（x+y），再进行离散傅立叶变换，即可将图像的频谱原点$（0，0）$移动到图像中心$（M／2,N／2）$处。  

3. 旋转不变性

  由旋转不变性，如果时域中离散函数旋转θ0​角度，则在变换域中该离散傅立叶变换函数也将旋转同样的角度。离散傅立叶变换的旋转不变性如下图所示。    
 

• 快速离散傅立叶变换

 
 
 
 
  由W 的周期性得：W4=W0，W6=W2，W9=W1；再由W的对称性可得：W3=−W1，W2=−W0。于是上述W 矩阵可变为：  
  可见$N=4$的$W$阵中只需计算W0和W1两个系数即可。这说明$W$阵的系数有许多计算工作是重复的，如果把一个离散序列分解成若干短序列， 并充分利用旋转因子W的周期性和对称性来计算离散傅立叶变换，便可以简化运算过程，这就是FFT的基本思想。  
 
 
 

• 例子：

 
 
 
 
 
 
 
  上述FFT是将$f(x)$序列按x 的奇偶进行分组计算的，称之为时间抽选FFT。   如果将频域序列的$F(u)$按**u 的奇偶进行分组计算， 也可实现快速傅立叶计算，这称为频率抽选FFT**。  

• 傅立叶变换应用的例子:

  傅里叶变换在图像处理中是一个最基本的数学工具。利用这个工具，可以对图像的频谱进行各种各样的处理，如滤波、降噪、增强等  
 

频域变换的一般表达式

  可分离变换
 
 

1. 二维傅立叶变换可以利用变换核的可分离性， 用两次一维变换来实现，即可先对$f(x,y)$的每一行进行一维变换得到$F(x,v)$，再沿$F(x,v)$每一列取一维变换得到变换结果$F(u,v)$。

  对于其他的图像变换，只要其变换核是可分离的，同样也可用两次一维变换来实现。   如果先对$f(x,y)$的每一列进行一维变换得到$F(y,u)$，再沿$F(y,u)$每一行取一维变换得到$F(u,v)$，其最终结果是一样的。该结论对反变换核也适用。  

离散余弦变换

• 离散余弦变换（Discrete Cosine Transform， DCT）的变换核为余弦函数。

• DCT除了具有一般的正交变换性质外， 它的变换阵的基向量能很好地描述人类语音信号和图像信号的相关特征。

• 余弦变换实际上是傅立叶变换的实数部分。

• 因此，在对语音信号、图像信号的变换中，DCT变换被认为是一种准最佳变换。

• 近年颁布的一系列视频压缩编码的国际标准建议中，都把DCT作为其中的一个基本处理模块。除此之外， DCT还是一种可分离的变换。

• 余弦变换主要用于图像的压缩，如目前的国际压缩标准的JPEG格式中就用到了DCT变换。

 
 
 
 
 
  通常根据可分离性， 二维DCT可用两次一维DCT来完成， 其算法流程与DFT类似。   离散余弦变换的计算量相当大， 在实用中非常不方便， 也需要研究相应的快速算法。目前已有多种快速DCT（FCT）， 比如由FFT的思路发展起来的FCT。  

• 性质：

  1 . 余弦变换是实数、正交。 2．离散余弦变换可由傅里叶变换的实部求得 3．对高度相关数据，DCT有非常好的能量紧凑性 4．对于具有一阶马尔可夫过程的随机信号，DCT是K-L变换 的 最好近似   • 在图像的变换编码中有着非常成功的应用   • 离散余弦变换是傅里叶变换的实数部分，比傅里叶变换有更强的信息集中能力。对于大多数自然图像，离散余弦变换能将大多数的信息放到较少的系数上去，提高编码的效率  

离散沃尔什哈达玛变换

  沃尔什函数：
 
 
 
 
  由哈达玛矩阵的特点可知，沃尔什-哈达玛变换的本质上是将离散序列$f(x)$的各项值的符号按一定规律改变后，进行加减运算， 因此，它比采用复数运算的DFT 和 采用余弦运算的DCT要简单得多。  
 
 
 
 
  我的微信公众号名称：深度学习与先进智能决策 微信公众号ID：MultiAgent1024 公众号介绍：主要研究分享深度学习、机器博弈、强化学习等相关内容！期待您的关注，欢迎一起学习交流进步！